Раздел 5. Линейные векторные пространства

41. Даны множества 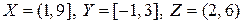. Найдите множества .

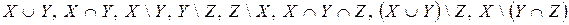42. Проверить, будет ли линейно независимой следующая система элементов: 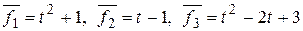на ?

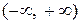43. Проверить, будет ли линейно независимой следующая система элементов: 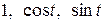на ?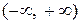

44. Найдите ранг системы элементов
.

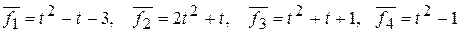45. Определить размерность линейной оболочки элементов
.

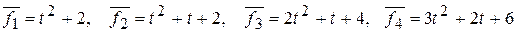46. Определить размерность линейной оболочки векторов .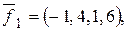

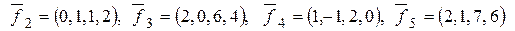47. Определить базис и размерность пространства решений системы

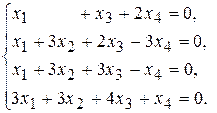
48. Доказать, что в пространстве 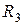элементы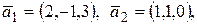 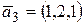образуют базис. Разложить элемент 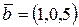по этому базису.

49. Пусть 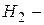пространство многочленов не выше второй степени. Доказать, что многочлены: 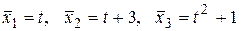образуют базис в 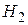. Разложить элемент 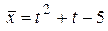по этому базису.

50. Найти координаты вектора 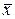в базисе 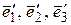, если , .

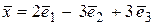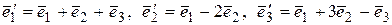51. Пусть 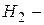пространство многочленов не выше второй степени. Найти матрицу перехода от базиса: 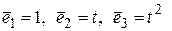к базису: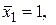 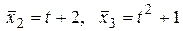. Разложить элемент 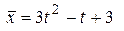по базису .

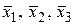52. В пространстве 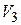базис 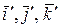получается из 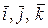поворотом вокруг вектора 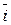на угол 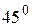против хода часовой стрелки. Найти матрицу перехода от 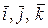к .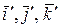

53. Доказать, что в пространстве 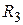элементы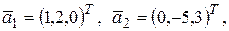 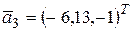образуют базис. Провести ортогонализацию по этого базиса.

54. Построить ортогональный базис линейной оболочки элементов
.

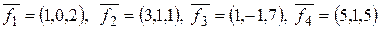55. Пусть 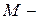линейная оболочка, натянутая на элементы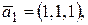 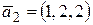. Для элемента 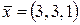найти его ортогональную проекцию на подпространство 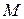и ортогональное дополнение.

56. Пусть 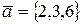. Доказать линейность оператора 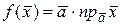в пространстве 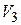и найти его матрицу в каноническом базисе.

57. Доказать, что в пространстве 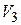оператор 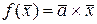, где 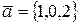, является линейным. Найти его ранг, ядро и дефект.

58. Пусть 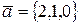. Доказать линейность оператора 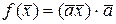в пространстве 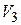. Найти его ранг, ядро и дефект.

59. В пространстве 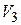оператор 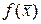осуществляет поворот вектора 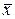вокруг оси 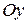на угол 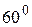. Найти матрицу оператора 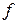в каноническом базисе.

60. В пространстве 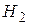задан оператор сдвига: 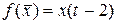, если 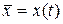. Найти матрицу этого оператора в каноническом базисе.

61. Пусть 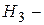пространство многочленов не выше третьей степени. В 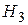задан оператор 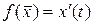. Найти матрицу оператора 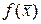в базисе .

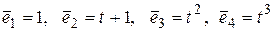62. В пространстве 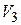оператор 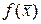осуществляет ортогональное проектирование вектора 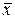на линейную оболочку векторов 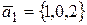, 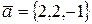. Найти матрицу оператора 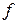в каноническом базисе.

63. В пространстве 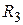заданы операторы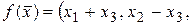
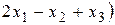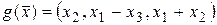, . Найти .

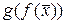64. Оператор 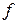в базисе. 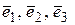имеет матрицу 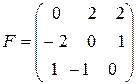. Найти матрицу оператора 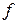в базисе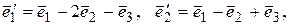
.

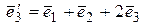65. Линейный оператор 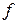в каноническом базисе имеет матрицу 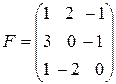. Найти матрицу оператора 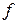в базисе , .

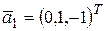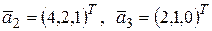66. Докажите, что оператор 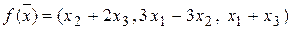, где 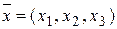, имеет обратный 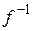. Найдите явный вид оператора .

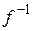67. Найти собственные значения и собственные векторы матрицы
.

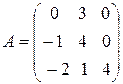68. Привести к каноническому виду квадратичную форму: 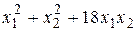. Какую замену переменных нужно сделать при этом?

69. Определить тип линии и найти ее центр:
.

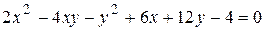70. Привести к каноническому виду квадратичную форму: 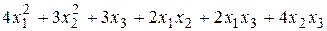. Какую замену переменных нужно сделать при этом?

71. Используя теорию квадратичных форм, определить тип поверхности, заданной уравнением 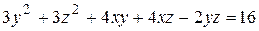.