Неинерциальные системы отсчета

В задачах, в которых идет речь о физических явлениях, происходящих внутри ускоренно движущегося тела (вагона, лифта, куска металла и т.д.), решение, основанное на применении второго закона Ньютона, упрощается, если рассматривать явление в неинерциальной системе отсчета, связанной с ускоренно движущимся телом. Соответственно двум движениям тела - поступательному и вращательному -применяют как поступательно движущиеся, так и вращающиеся неинерциальные системы отсчета. Тогда для записи второго закона Ньютона водят силы инерции.

Существует другой способ объяснить поведение тела в неинерциальной системе отсчета, движущейся поступательно (или вращающейся, если рассматриваемая материальная точка в ней покоится). При этом никаких сил инерции не вводят, но считают, что происходит изменение поля тяготе­ния: ускорение силы тяжести изменяется по модулю и направлению.

Из двух рассмотренных методов второй гораздо быстрее приводит к цели в тех случаях, когда искомая величина определяется в неинерциальной системе отсчета какой-либо известной формулой, содержащей ускорение силы тяжести.

Примеры решения задач по механике

1. Тело вращается вокруг неподвижной оси по закону, выражаемому формулой 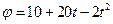. Найти по величине и направлению полное ускорение точки, находящейся на расстоянии 0,1 м от оси вращения, для момента времени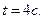

Решение. Точка вращающегося тела описывает окружность, Полное ускорение точки, движущейся по кривой линии, может быть найдено как геометрическая сумма тангенциального ускорения 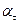,направленного по касательной к траектории, и нормального ускорения 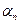, направленного к Центру кривизны траектории:

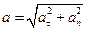. (1)

Тангенциальное и нормальное ускорения точки вращающегося тела выражаются формулами:

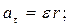(2)

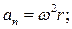(3)

где 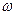- угловая скорость тела; 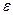- его угловое ускорение; r - расстояние точки от оси вращения. Подставляя выражения 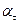и 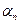в формулу (1). находим:

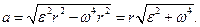(4)

Угловая скорость 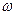вращающегося тела равна первой производной от угла поворота по времени: 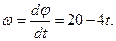В момент времени t = 4 с угловая скорость, 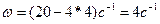. Угловое ускорение вращающегося тела равно первой производной от угловой скорости по времени: 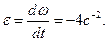Это выражение углового ускорения не содержит времени: следовательно, угловое ускорение имеет постоянное значение, не зависящее от времени.

Подставляя найденные значения 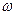и 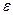и заданное значение 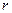в формулу (4), получим: 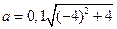м/с²=1,65 м/с².

Направление полного ускорения определится, если найти углы, которые вектор ускорения образует с касательной к траектории или с нормалью к ней (рис.1)

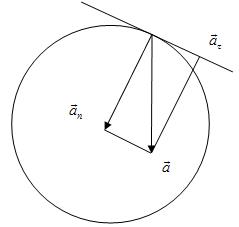
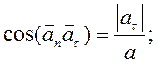(5)

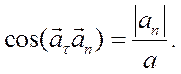(6)

По формулам (2) и (3) найдем значения 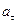и :

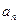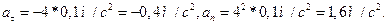
Подставляя эти значения и значение полного ускорения в формулы (5) и (6):

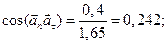
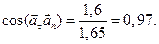
Пользуясь тригонометрическими таблицами, найдем значения искомых углов:

,

.

Uy

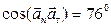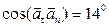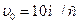2. Мяч брошен со скоростью под углом 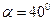к горизонту. На какую высоту h поднимется мяч? На каком расстоянии l от места бросания он упаяет на землю? Какое время t он будет в движении?

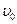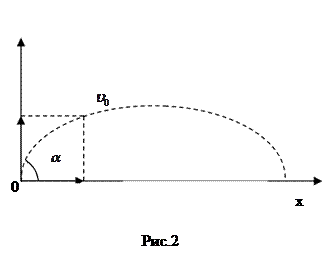
Найдем высоту h, на которую поднимется мяч, брошенный со скоростью под углом 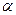к горизонту. Имеем (рис 2)

(1)

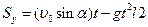(2)

В верхней точке 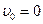, из (1) получим 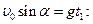отсюда время подъема мяча 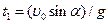. Подставляя 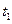в (2), получим

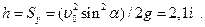
Найдем дальность полета l мяча. Имеем (рис 2)

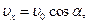(3)

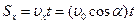(4)

Мяч упадет, на землю через время 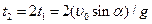. Подставляя 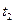в (4), получим 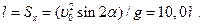Время полета мяча

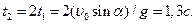
3. Колесо радиусом R=10,0 см вращается с угловым ускорением 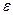=3,14 рад/с². Найти для точек на ободе колеса к концу первой секунды. после начала движения: а) угловую скорость 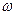; б) линейную скорость 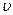;в) тангенциальное ускорение 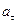; г) нормальное ускорение 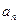; д) полное ускорение 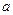; е) угол 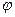, составляемый вектором полного ускорения с радиусом колеса.

а) При равнопеременном вращательном движении угловая скорость 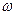связана с временем t уравнением 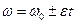. По условию 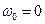и тогда 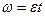, т.е. угловая скорость растет пропорционально времени; при 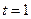с имеем 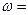3,14-рад/с.

б) Так как 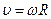, то линейная скорость также пропорциональна времени; 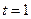с имеем 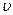= 0,314 м/с.

в) Тангенциальное ускорение 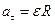не зависит от t т.е. постоянно во все время движения: при t = 1с имеем 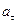= 0,314 м/с².

г) Нормальное ускорение 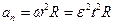, т.е. растет пропорционально квадрату времени; при t = 1с имеем 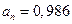м/с².

д) Полное ускорение растет со временем по закону

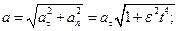
при t = 1с имеем 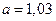м/с².

е) Имеем 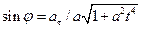, где 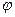-угол, составляемый вектором полного ускорения с радиусом колеса. В начальный момент t = 0 имеем 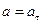- полное ускорение направлено по касательной. При 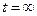имеем 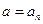(так как 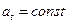и 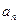пропорционально квадрату времени) - полное ускорение направлено по нормали. К концу первой секунды 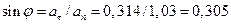и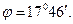

4. Какой- массы т_х балласт надо сбросить с равномерно опускающегося аэростата, чтобы он начал равномерно подниматься с той же скоростью? Масса аэростата с балластом т = 1600 кг, подъемная сипа аэростата F = 12,00 кН. Считать силу сопротивления F_conp воздуха одной и той же при подъеме и при спуске.

На опускающийся аэростат (с балластом) действуют подъемная сила F (вверх), сила сопротивления воздуха F_conp (вверх) и сила тяжести 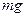(вниз). Так как аэростат движется равномерно, то по первому закону Ньютона равно действующая сила равна нулю:

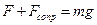. (1)

Когда балласт сброшен и аэростат начнет подниматься, вместо уравнения (1) будем иметь

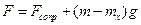; (2)

решая (1) и (2) совместно, получим 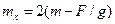=800 кг.

5. Автомобиль массой т = 1020 кг. двигаясь равнозамедленно, останавливается через время 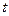= 5,00 с, пройдя путь s= 25.0 м. Найти начальную скорость 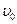автомобиля и силу торможения F.

Задачу можно решить двумя способами.

1). По второму закону Ньютона

F = т а, (1)

где F - сила торможения, т - масса автомобиля, а -его ускорение. Из уравнений кинематики равнопеременного движения получим

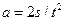, (2)

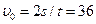км/ч. (3)

Подставляя (2) в (1), имеем

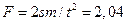кН. (4)

2) Используем закон сохранения энергии. Убыль кинетической энергии равна работе силы торможения

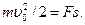(5)

Но из уравнений кинематики имеем 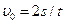. Подставляя (3) в (5), получим, как и раньше. .

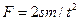6. На автомобиль массой т = 1 т во время движения действует сила трения 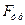равная 0,1 действующей, на него силы тяжести т 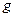. Найти силу тяги F, развиваемую мотором автомобиля, если автомобиль движется с постоянной скоростью: а) в гору с уклоном 1 м на каждые 25 м пути; б) под гору с тем же уклоном.

а) Сила тяги, развиваемая мотором автомобиля, поднимающегося в гору. идет на преодоление силы трения и составляющей силы тяжести, параллельной перемещению: 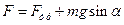, причем 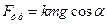. Таким образом, сила тяги F = т 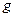(k cos 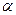+ sin 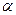) = 1,37 кН.

б) Для автомобиля, движущегося под гору, сила тяги

F = т 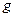(k cos 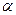- sin 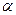) = 0,59 кН.

Если сила трения меньше составляющей силы тяжести, параллельной перемещению, т.е. если k т g cos 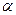< т g sin 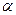, то F < 0. В этом случае, чтобы осуществить равномерное движение автомобиля поя гору, необходимо приложить задерживающую силу. При отсутствии этой сипы автомобиль будет двигаться под гору с ускорением 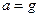(sin 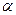- k cos ).

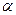7. На рельсах стоит платформа массой т₁ = 10 т. На платформе закреплено орудие массой т₂ = 5т, из которого производится выстрел вдоль рельсов. Масса снаряда т₃=100 кг: его начальная скорость относительно орудия 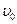= 500 м/с. Найти скорость платформы в первый момент после выстрела, если а) платформа стояла неподвижно; б) платформа двигалась со скоростью = 18 км/ч и выстрел был произведен в направлении, ее движения; в) платформа двигалась со скоростью = 13.км/ч и выстрел был произведен в направлении, противоположном направлению ее движения.

Согласно закону сохранения импульса

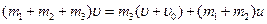
(скорость снаряда относительно Земли равна 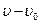). Отсюда

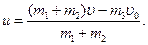
Спроецировав векторы на ось х, совпадающей по направлению с вектором 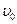, получим

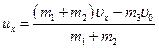
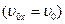
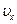а) , а следовательно и , равна нулю; 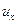=-12 км/ч. Проекция и на ось х получилась отрицательной. Это означает, что вектора 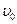и и противоположны.

б) 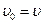; и_х = 6 км/ч. Платформа движется в первоначальном направлении, но с меньшей скоростью.

в) 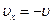; и_х =-30 км/ч. Платформа движется в первоначальном направлении с большей скоростью.

8. Шар массой т₁=3 кг движется со скоростью 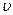= 4 м/с и ударяется о неподвижный шар такой же массы. Считая удар центральным и абсолютно неупругим, найти количество теплоты Q, выделившееся при ударе.

Первый шар до удара обладал кинетической энергией 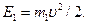После удара шары начали двигаться с обшей скоростью 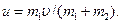Кинетическая энергия обоих шаров после удара стала 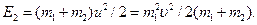Разность Е₁-Е₂. равна количеству теплоты Q, выделившейся при ударе:

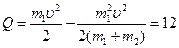Дж.

9. Найти первую космическую скорость 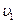, т.е. скорость, которую надо сообщить телу у поверхности Земли, чтобы оно начало двигаться вокруг Земли по круговой орбите в качестве ее спутника.

Сила гравитационного взаимодействия между телом и Землей 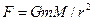,где 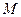- масса Земли и 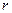-расстояние тела от центра Земли. У поверхности Земли 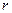равно радиусу Земли R и 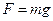. Следовательно,

.

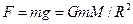При движения тела вокруг Земли по орбите сила гравитационного взаимодействия является центростремительной силой. Таким образом, 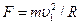: отсюда первая космическая скорость 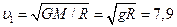м/с.

10. Найти линейные ускорения а центров шара, диска и обруча, скатывающихся без скольжения с наклонной плоскости. Угол наклона плоскости 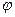= 30°, начальная скорость всех тел 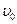= 0. Сравнить найденные ускорения сускорением тела, соскальзывающего с наклонной плоскости при отсутствии трения.

При скатывании тела с наклонной плоскости его потенциальная энергия переходит в кинетическую. Таким образом,

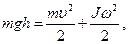(1)

где J - момент инерции тела и m - его масса, Но

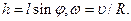(2)

Подставляя (2) в (1), получим

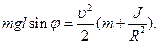(3)

Так как движение тел происходит под действием постоянной силы, то движение тел равноускоренное, поэтому

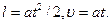(4)

Решая (3) и (4) совместно, получим

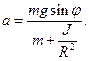(5)

Подставляя в (5) выражения для момента инерции различных тел, найдем для шара, диска и обруча соответственно

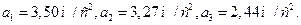
Для тела, соскальзывающего с наклонной плоскости без трения, имеем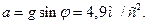

11. Горизонтальная платформа массой m = 100 кг вращается вокруг вертикальной оси, проходящей через центр платформы, с частотой 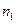= 10 об/мин. Человек массой m₀ = 60 кг стоит при этом на краю платформы. С какой частотой п₂ начнет вращаться платформа, если человек перейдет от края платформы к ее центру? Считать платформу однородным диском, а человека = точечной массой.

На основании закона сохранения момента количества движения имеем

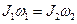, (1)

где 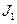- момент инерции платформы с человеком, стоящим на ее краю.

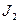- момент инерции платформы с человеком, стоящим в центре платформы, 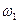и 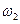угловые скорости платформ в первом и во втором положениях человека, При этом

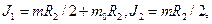(2)

где R - радиус платформы. Подставляя (2)в (1) и учитывая, что 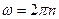, где 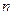- частота вращения платформы, получим

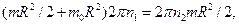
откуда 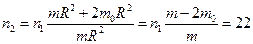об/мин.

12. При выстреле из пружинного пистолета вертикально вверх пуля массой т = 20 г поднялась на высоту 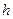= 5 м. Определить жесткость k пружины пистолета, если она была сжата на s = 10 см. Массой пружины пренебречь.

Для решения задачи воспользуемся законом сохранения энергии в механике. Но прежде проследим за энергетическими превращениями, с которыми связан выстрел.

При зарядке пистолета сжимается пружина. При этом совершается работа А₁,в результатечего пружина приобретает потенциальную энергию Т₂. При выстреле потенциальная энергия пружины переходит в кинетическую энергию Т₂ пули, а затем при подъеме ее на высоту h .превращается в потенциальную энергию П₂ пули.

Если пренебречь потерями энергии в этой «цепочке» энергетических превращений, то на основании закона сохранения энергии можно записать

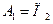. (1)

Выразим работу A₁. Сила 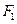, сжимающая пружину, является переменной - в каждый данный момент она по направлению противоположна силе упругости F и численно равна ей. Сила упругости, возникающая в пружине при ее деформации, определяется по закону Гука

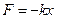, (2)

где х - абсолютная деформация пружины.

Работу переменной силы вычислим как сумму элементарных работ. Элементарная работа при сжатии пружины на dx выразится формулой

,

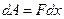или

.

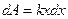Интегрируя в пределах от 0 до 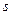, получим

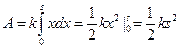. (3)

Потенциальная энергия пули на высоте h определится по формуле

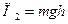, (4)

где g - ускорение свободного падения.

Подставив в (1) А₁ по (3) и П₂ по (4), найдем 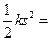mgh, откуда

.

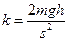Проверим, дает ли полученная формула единицу измерения жесткости k. Для этого в правую часть формулы (5) вместо величин подставим единицы их измерения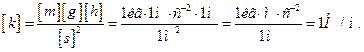

Теперь можем подставить в (5) числовые значения и произвести вычисления