Определение предела функции

Пусть aÎR или a = ±¥.

Число A = 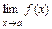называется пределом функции f при стремлении x к a, если для любой окрестности U (A,e) существует проколотая окрестность точки a (a, d), для каждой точки x из которой выполняется условие f(x) Î U (A,e):

" U (A,e) $ (a, d): (x Î (a, d) Þ f(x) Î U (A,e)).

Замечание. Для того чтобы можно было говорить о пределе функции f(x) при x ® a, необходимо чтобы функция f(x) была определена в некоторой проколотой окрестности точки a. Предел последовательности можно рассматривать только при n ® ¥, так как любая окрестность U(+¥, d) точки +¥ содержит все натуральные числа n > d, и, следовательно, последовательность определена в этой окрестности, а для любой конечной точки а можно найти достаточно малую окрестность, которая не содержит ни одного натурального числа.

Рассмотрим, как можно сформулировать определение предела функции на языке неравенств.

Заметим, что все окрестности (a, d) точки а отличаются друг от друга только величиной d, а все окрестности U (A,e) точки А— величиной e.

Пусть = А ¹ ± ¥, то есть а = х₀ ¹ ± ¥ и А ¹ ± ¥.

В этом случае определение предела

" U (A,e) $ (x₀, d): (x Î (x₀, d) Þ f(x) Î U (A,e))

можно переписать в виде

" e > 0 $ d > 0: (0 ¹ |x – x₀| < d Þ |f(x) – A| < e).

Если = А ¹ ± ¥, то есть а = + ¥ и А ¹ ± ¥, получаем

" e > 0 $ d > 0: (x > d Þ |f(x) – A| < e).

Если и = +¥, то есть а = – ¥ и A = +¥, получаем

" e > 0 $ d > 0: (x < – d Þ f(x) > e).

В качестве упражнений получите определение предела функции на языке неравенств для случаев: а = х₀, А = ± ¥; а = + ¥, А = ± ¥; а = – ¥, А ¹ ± ¥, А = – ¥.

Если в определении предела вместо проколотой окрестности (a, d) использовать односторонние окрестности (x₀ + 0, d) или (x₀ – 0, d), получим определения односторонних пределов.

Число A = называется правосторонним пределом или пределом функции f(x) в точке x₀ справа, если для любой окрестности U (A,e) существует правосторонняя окрестность точки x₀ ( x₀ + 0, d), для каждой точки x из которой выполняется условие f(x) Î U (A,e):

" U (A,e) $ ( x₀ + 0, d): (x Î ( x₀ + 0, d) Þ f(x) Î U (A,e)).

Число A = называется левосторонним пределом или пределом функции f(x) в точке x₀ слева, если для любой окрестности U (A,e) существует левосторонняя окрестность точки x₀ ( x₀ – 0, d), для каждой точки x из которой выполняется условие f(x) Î U (A,e):

" U (A,e) $ ( x₀ – 0, d): (x Î ( x₀ – 0, d) Þ f(x) Î U (A,e)).

,

.

ТЕОРЕМА. Критерий существования предела.

Для того чтобы функция f (x) имела в точке x₀ конечный предел, необходимо и достаточно, чтобы в этой точке существовали ее конечные односторонние пределы, равные между собой.

ДОКАЗАТЕЛЬСТВО.

Пусть существует 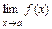= А. Докажем, что существуют

и .

Возьмем произвольное e > 0. Так как 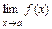= А, то существует проколотая окрестность (a, d) точки а, для каждой точки х из которой f(x) Î U (A,e). Поскольку (a, d) совпадает с объединением односторонних окрестностей (a – 0, d) и (a + 0, d) того же радиуса d, то для каждой точки х из окрестностей (a – 0, d) и (a + 0, d) выполняется условие f(x) Î U (A,e). В силу произвольности e имеем

= А и = А.

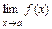Пусть теперь существуют и . Докажем, что существует = А.

Возьмем произвольное e > 0. Так как и , то существуют односторонние окрестности (a – 0, d₁) и (a + 0, d₂), для каждой точки х из которых f(x) Î U (A,e). Возьмем число d = min {d₁, d₂}. Тогда окрестность (a, d) содержится в объединении (a – 0, d₁) (a + 0, d₂), и, следовательно, для каждой точки x из (a, d) выполняется условие f(x) Î U (A,e). В силу произвольности e имеем 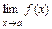= А. Теорема доказана.