Строки первой матрицы- сомножителя на соответствующие элементы j-го
столбца второй матрицы-сомножителя.
Из сказанного следует, что если можно найти произведение матриц AB, то произведение BA, вообще говоря, не определено.
Приведем примеры перемножения матриц:
1) 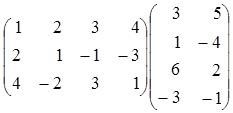 =
=
= 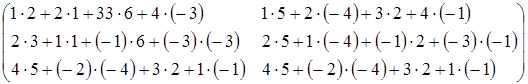 =
=
= 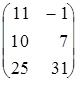 ;
;
2) 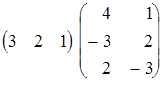 = (8, 4).
= (8, 4).
Если AB и BA одновременно определены, то, вообще говоря, эти произведения не равны. Это означает, что умножение матриц не коммутативно. Продемонстрируем это на примере.
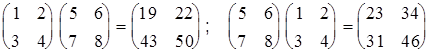 .
.
Для алгебраических действий над матрицами справедливы следующие законы:
1) A + B = B+ A;
2) a (A + B) = aA + aB;
3) (A +B) + C = A + (B + C);
4)(AB)C = A(BC);
5)A(B + C) =AB + AC.
Матрица, состоящая из одной строки, называется вектором (вектором-строкой). Матрица, состоящая из одного столбца, также называется вектором (вектором-столбцом).
Пусть имеется матрица A = (aij) размерности m ´ n, n-мерный вектор-столбецX и m-мерный вектор-столбец B:
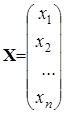 ;
; 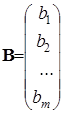 .
.
Тогда матричное равенство
AX = B, (1)
если расписать его поэлементно, примет вид:
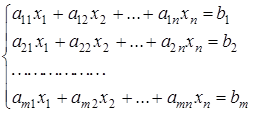 .
.
Таким образом, формула (1) является записью системы m линейных уравнений с n неизвестными в матричной форме. Ниже будет показано, что, записывая систему в сжатом виде, кроме краткости написания мы получаем и другие очень важные преимущества.
Пусть имеются две квадратные матрицы одинаковой размерности:
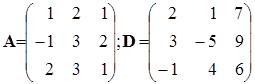 .
.
Требуется найти матрицу X, удовлетворяющую матричному уравнению
AX = D.
Из правила умножения матриц следует, что матрица X должна быть квадратной матрицей той же размерности, что и матрицы A и D:
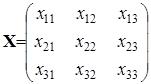 .
.
Из правила умножения матриц и из определения равенства матриц следует, что последнее матричное уравнение распадается на три системы линейных уравнений:
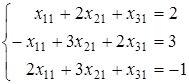 ;
;
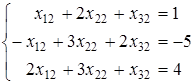 ; (2)
; (2)
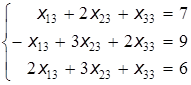 .
.
Все три системы (2) имеют одинаковые матрицы коэффициентов, что дает возможность решать их одновременно, введя матрицу

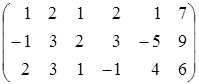 .
.
Здесь первые четыре столбца образуют расширенную матрицу первой системы, первые три столбца вместе с пятым столбцом образуют расширенную матрицу второй системы, а первые три столбца вместе с шестым – расширенную матрицу третьей системы.
Применим для решения метод Жордана-Гаусса который является модификацией метода Гаусса.
Первый шаг преобразования матрицы по методу Жордана-Гаусса совпадает с первым шагом преобразований по методу Гаусса. Оставляем без изменений первую строку матрицы, а во второй и третьей “организуем” нули в первом столбце:

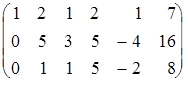 .
.
Теперь, следуя методу Жордана-Гаусса, оставляем без изменения лишь вторую строку (так как a22 ¹ 0) и получаем с помощью второй строки в первой и третьей строках во втором столбце нули. Для этого вместо первой строки пишем сумму первой строки, умноженной на 5, и второй строки, умноженной на –2. Вместо третьей строки пишем сумму третьей строки , умноженной на 5, и второй строки, умноженной на –1 После деления полученной третьей строки на 2 получаем матрицу
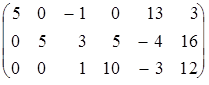 .
.
Чтобы в первой и второй строках в третьем столбце получить нули, проведем следующие преобразования последней матрицы. Оставив третью строку без изменений, заменим вторую строку разностью второй строки и утроенной третьей, а первую – суммой первой и третьей строк. После деления первой и второй строк преобразованной матрицы на 5 получится матрица
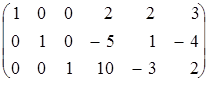 . (3)
. (3)
При преобразовании системы по методу Жордана-Гаусса матрица коэффициентов приводится (если это возможно) к такому виду, что на главной диагонали стоят единицы, а над главной диагональю и под главной диагональю – нули.
Если взять первые четыре столбца матрицы (3), то получится матрица, в которую преобразовалась расширенная матрица первой из систем уравнений (2). Из нее следует: x11=2; x21=–5; x31=10. Матрица, образованная первыми тремя столбцами вместе с пятым столбцом матрицы (3), дает решение второй системы уравнений (2): x12=2; x22=1; x32=–3. И, наконец, матрица, образованная первыми тремя столбцами вместе шестым столбцом матрицы (3), дает решение третьей системы уравнений (2): x13=3; x23=–4; x33=12.
Из сказанного можно сделать очень интересный и важный вывод: последние три столбца матрицы (3) образуют искомую матрицу X.
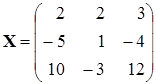 .
.
Введем ряд новых определений.
Нулевой матрицейназывается матрица, у которой все элементы – нули. Очевидно равенство A+ (–1)A = 0. Здесь в правой части через 0 обозначена нулевая матрица той же размерности, что и матрица A.
Квадратная матрица размера n называется единичной, если все её элементы, стоящие на главной диагонали, равны единице, а все остальные – нули. Единичную матрицу можно определить формулами:
aij = 1 при i = j;
aij = 0 при i ¹ j.
Очевидно, что первые три столбца матрицы (3) образуют единичную матрицу.
Единичная матрица, как правило, обозначается буквой E:
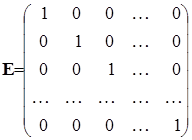 .
.
Легко проверить справедливость равенств: EA = AE = A. Здесь A – квадратная матрица, и размеры A и E одинаковы.
Пусть A – квадратная матрица. Обратной матрицейк матрице Aназывается такая матрица A–1, для которой справедливы равенства:
AA–1 = A–1A = E.
Очевидно, что A–1 – квадратная матрица того же размера, что и матрица A. Сразу заметим, что не всякая квадратная матрица имеет обратную матрицу.
Поставим задачу: найти обратную матрицу к матрице
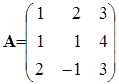 .
.
Условие
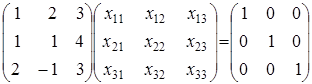 ,
,
где
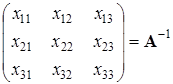 ,
,
сводится к трём системам уравнений, которые будем решать одновременно, используя метод Жордана-Гаусса. Матрица, представляющая расширенные матрицы всех трёх систем, примет вид
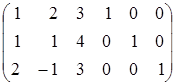 .
.
Подвергая её преобразованиям по методу Жордана-Гаусса, последовательно будем получать:
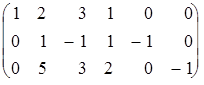 Þ
Þ 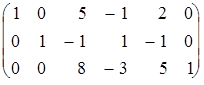 Þ
Þ
Þ 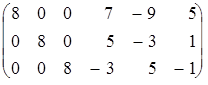 Þ
Þ 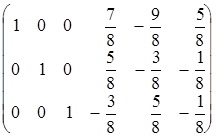 (4)
(4)
Как и в предыдущем примере, можно сказать, что три последних столбца образуют искомую матрицу, то есть
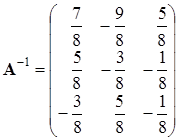 .
.
Теперь сформулируем правило, по которому находится матрица, обратная к квадратной матрицеА размера n.
Нужно выписать матрицу размерности n ´ 2n, первые n столбцов которой образованы матрицей А, а последние n столбцов образуют единичную матрицу Е. Построенная таким образом матрица преобразуется по методу Жордана-Гаусса так, чтобы на месте матрицы А получилась единичная матрица, если это возможно. Тогда на месте матрицы Е получается матрица А–1.
Если матрицу Анельзя методом Жордана-Гаусса преобразовать к единичной матрице, то А–1 не существует. Так матрица
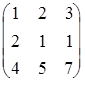
не имеет обратной. Читатель может в этом убедиться самостоятельно.
Определители
Рассмотрим систему двух линейных уравнений с двумя неизвестными в общем виде:
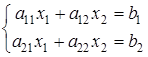 .
.
Найдем x1 следующим образом: чтобы исключить x2, умножим первое уравнение на a22 и из полученного уравнения вычтем второе, умноженное на a12:
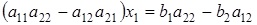 . (1)
. (1)
Обозначим D = a11a22 – a12a21, D1 = b1a22 – b2a12.
Для определения x2 поступим так: умножим второе уравнение на a11 и из полученного уравнения вычтем первое, умноженное на a21:
(a11a22 – a12a21)x2 = a11b2 – a21b1. (2)
Обозначим D2 = a11b2 – a21b1.
Из (1) и (2) видно, что если D ¹ 0, то система имеет единственное решение[1], определяемое формулой
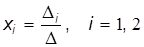 . (3)
. (3)
Величина D называется определителем матрицы второго порядка
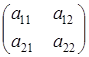 .
.
Вообще определителем произвольной матрицы второго порядка 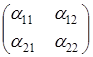 называется число, которое обозначается
называется число, которое обозначается 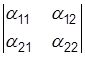 и равно произ
и равно произ
ведению двух чисел, стоящих на главной диагонали минус произведение двух чисел, стоящих на другой диагонали: a11a22 – a12a21.
Например,
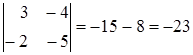 .
.
Из сказанного следует, что величины D1 и D2 в (3) тоже являются определителями:
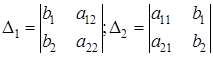 .
.
Рассмотрим теперь систему трех линейных уравнений с тремя неизвестными:
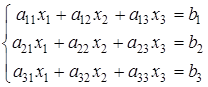 . (4)
. (4)
Введем определение. Определителем произвольной квадратной матрицы третьего порядка 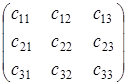 называется сумма шести слагаемых, каждое из которых представляет собой произведение трех элементов матрицы, выбираемых по следующему правилу: три произведения элементов, стоящих на главной диагонали и в вершинах двух треугольников:
называется сумма шести слагаемых, каждое из которых представляет собой произведение трех элементов матрицы, выбираемых по следующему правилу: три произведения элементов, стоящих на главной диагонали и в вершинах двух треугольников:  , берутся со знаком "+", а три произведения элементов, стоящих на второй диагонали и в вершинах двух других треугольников:
, берутся со знаком "+", а три произведения элементов, стоящих на второй диагонали и в вершинах двух других треугольников:  , берутся со знаком "-". Определитель третьего порядка обозначается так:
, берутся со знаком "-". Определитель третьего порядка обозначается так:
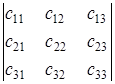 .
.
Например,
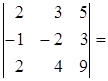
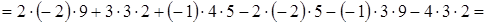
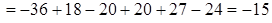
Решая систему (4), например методом Гаусса, можно получить равенства
D×x1 = D1; D×x2 = D2; D×x3 = D3, (5)
где
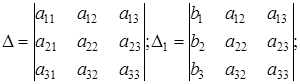
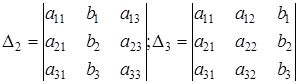 .
.
Из формул (5) видно, что если D ¹ 0, то единственным образом определяется решение системы:
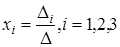 .
.
Решая квадратные системы линейных уравнений 4-го, 5-го или любого более высокого порядка, можно получить формулы, аналогичные формулам (1), (2) или (5).
Дадим определение определителя
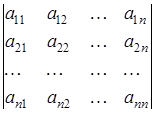
квадратной матрицы n-го порядка или просто определителя n-го порядка. (В дальнейшем, принимая во внимание введённое обозначение, под элементами, строками и столбцами определителя матрицы будем подразумевать элементы, строки и столбцы этой матрицы.)
Сформулируем понятие n! (читается эн факториал): еслиn– натуральное (целое положительное) число, тоn!– это произведение всех натуральных чисел от1доn.
n! = 1×2×3×¼×(n – 1) n.
Например,
5! = 1×2×3×4×5 = 120.
Замечание: в некоторых книгах вместо термина "определитель" используется термин "детерминант" и определитель матрицы A обозначается detA.
Определителемn-го порядка называется сумма n! слагаемых. Каждое слагаемое представляет собой произведениеnэлементов, взятых по одному из каждой строки и каждого столбца определителя[2] . (Произведения отличаются одно от другого набором элементов.)Перед каждым произведением ставится
знак "+" или "-". Покажем, как определить, какой нужно ставить знак перед
произведением.
Так как в каждом произведении присутствует один элемент из 1-й строки, один элемент из 2-ой и т.д., то произведение в общем виде можно записать так:
a1i×a2j×a3k×¼×ans.
Здесь i, j, k, ¼, s – номера столбцов, в которых стоят элементы, выбранные из 1-й, 2-й, 3-й, ... n-й строк, соответственно. Ясно из сказанного выше, что каждое из чисел i, j, k, ¼, s равно какому-либо из чисел 1, 2, ..., n, и что все числа i, j, k, ¼, s – различные.
Расположенные в данном порядке
i, j, k, ¼, s,
эти числа образуют "перестановку" из чисел 1, 2, ..., n (перестановкой называется заданный порядок в конечном множестве).
Взаимное расположение двух чисел в перестановке, когда большее стоит впереди меньшего называется инверсией. Например, в перестановке 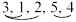 три инверсии; в перестановке
три инверсии; в перестановке 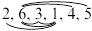 – шесть инверсий.
– шесть инверсий.
Перестановка называется четной, если в ней четное число инверсий и нечетной, если число инверсий нечетное.
Теперь можно сформулировать правило: произведениеa1i×a2j×a3k×¼×ans берется со знаком "+", если вторые индексы образуют четную перестановку, и со знаком "-", если нечетную.
Из определения определителя можно вывести следующие его свойства.
