Расчет структуры осесимметричных стационарных
Реферат
Отчет о курсовой работе: 32 с.,10 рис., 1 табл., 3 приложения, 3 источника.
Объекты исследования — шарообразная плоскость в диэлектрической среде и прямоугольный волновод с волной Е52.
Цель работы – расчет структуры полей проводящего шара в диэлектрической среде, а также в волноводе для приведенных в задании параметров.
Метод исследования – метод разделения переменных при интегрировании дифференциальных уравнений для получения аналитических выражений потенциалов и напряженностей полей с последующим построением на ЭВМ структуры этих полей.
Для заданной геометрии и параметров среды получены аналитические выражения значений потенциалов и напряженностей полей внутри и вне шара, а так же выражение для расчета вектора электрической индукции вне шара. В случае волны Е52 распространяющейся в прямоугольном волноводе сечением 72х34 мм, путем интегрирования волнового уравнения и использования уравнений Максвелла получены соотношения, описывающие поведение поперечных и продольных компонент полей, а также выражения для расчета коэффициента распространения 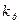 в волноводе и эквивалентного сопротивления
в волноводе и эквивалентного сопротивления 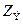 . Построены картины структуры статических полей для шара и переменных полей для волновода. Рассчитано значения вектора электрической индукции вне шара в точке М и проанализированы полученные для волновода результаты.
. Построены картины структуры статических полей для шара и переменных полей для волновода. Рассчитано значения вектора электрической индукции вне шара в точке М и проанализированы полученные для волновода результаты.
Ключевыми словами в этой работе являются: поле, волна, коэффициент распространения, эквивалентное сопротивление, критическая частота.
Содержание
Реферат…………………………………………………………………………………3
Содержание……………………………………………………….…………………...4
Перечень условных обозначений, символов, единиц, сокращений и
терминов……………………………………………………...……………………….5
Введение………………………………………………………………………..……...6
1.Расчет структуры осесимметричных стационарных электромагнитных полей
· Общее задание…………………………………………………………….........7
· Параметры задачи………………………………………………………………7
· Решение…………………………………………………………………………7
2.Расчет структуры переменных электромагнитных полей в волноводе
Общее задание………………………………...……………………………..........16
· Параметры задачи……………..………………………………………………16
· Решение……………..…………………………………………………………16
Выводы……………..…………………………………………..……………….........31
Перечень ссылок……………..………………………………………………………32
Приложение А
Приложение Б
Приложение В
Введение
Электромагнитное поле – это вид материи, определяемый во всех точках двумя векторными величинами, которые характеризуют две ее стороны, называемые соответственно электрическим полем и магнитным полем, и оказывающий силовое воздействие на заряженные частицы, зависящее от их скорости и заряда.
Основным математическим аппаратом при расчете электромагнитного поля является векторный анализ, который включает в себя понятия “скаляр”, ”вектор” и ”тензор”. В общем случае скаляры и векторы являются функциями координат точки и времени.
При анализе электромагнитного поля применяются линейные, поверхностные и объемный интегралы, а также дифференциальные операторы. Дифференциальные операторы позволяют сократить запись различных операций над скалярными и векторными величинами. Электромагнитное поле может самостоятельно существовать в виде электромагнитных волн в пустоте. Это свидетельствует о том, что оно является особой формой материи. В тоже время электромагнитное поле обладает энергией, массой и количеством движения, то есть характеристиками обычной формы материи. При распространении электромагнитного поля одновременно с движением потока электромагнитной энергии происходит движение массы поля и количества движения.
В одних случаях электромагнитное поле характеризуется непрерывным распределением в пространстве, а в других случаях обнаруживает дискретность своей структуры, проявляющуюся в виде квантов излученного поля.
Теория электромагнитного поля представляет собой учение об электрических и магнитных явлениях, о теоретических положениях и законах, которым подчиняются эти явления, и о вытекающих из них методах расчета.
Изучение видов полей (электростатическое поле, электрическое поле постоянного тока в проводящей среде, магнитное поле постоянного тока, переменное электромагнитное поле) расширяет физические представления о поле, известные из курса физики, способствует более глубокому пониманию процессов, происходящих в электротехнических установках, а также важно с прикладной точки зрения, поскольку оно дает возможность решать многие задачи, имеющие существенное значение не только для теории электрических цепей, но и для решения задач, которые выходят за рамки данного курса и имеют самостоятельное значение.
Расчет структуры осесимметричных стационарных
Электромагнитных полей.
Общее задание:
Осесиметричное тело радиуса r находится в однородном внешнем электрическом поле 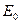 , перпендикулярном к его оси. Заданы характеристики окружающей среды. Получить аналитические выражения для потенциалов
, перпендикулярном к его оси. Заданы характеристики окружающей среды. Получить аналитические выражения для потенциалов 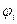 и
и 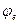 и полей
и полей 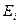 и
и 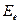 соответственно внутри и вне тела. Для заданных численных значений параметров задачи построить симейство эквипотенциальных линий в плоскости, перпендикулярной оси симметрии тела.
соответственно внутри и вне тела. Для заданных численных значений параметров задачи построить симейство эквипотенциальных линий в плоскости, перпендикулярной оси симметрии тела.
Найти вектор электрической индукции 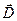 в точке М.
в точке М.
Параметры задачи:
Шарообразная плоскость в диэлектрической среде: r=4 см; 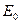 =15 кВ/м;
=15 кВ/м; 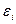 =1;
=1; 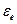 =7. Координаты точки М:
=7. Координаты точки М: 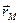 =5 см;
=5 см; 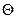 =
= 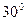
Решение:
В данной задаче граничная поверхность- сфера, поэтому будем пользоваться сферической системой координат. Тогда 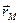 - радиус-вектор точки наблюдения, ось z направлена вдоль приложенного электрического поля (рис. 1.1).
- радиус-вектор точки наблюдения, ось z направлена вдоль приложенного электрического поля (рис. 1.1).
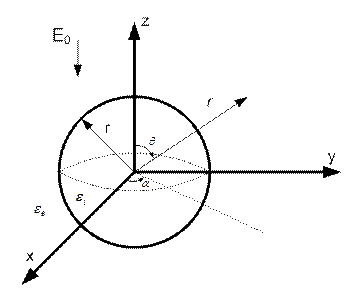
рис. 1.1
Внутри и вне шара сторонних зарядов нет, поэтому следует решать уравнение Лапласа 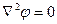 с соответствующими граничными условиями на поверхности.
с соответствующими граничными условиями на поверхности.
В данной задаче поле не зависит от координаты 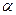 , поэтому поле будет описываться уравнением [1.560]:
, поэтому поле будет описываться уравнением [1.560]:
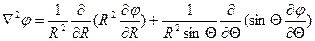
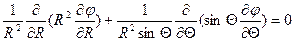 (1.1)
(1.1)
Применим метод Фурье-Бернулли для решения уравнения (1.1):
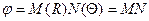 (1.2)
(1.2)
Подставим (1.2) в (1.1), учтя что:
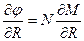 ;
; 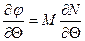 (1.3)
(1.3)
Получаем:
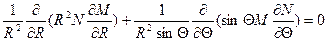
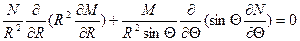 (1.4)
(1.4)
Умножим (1.4) на 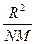 :
:
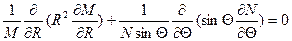 (1.5)
(1.5)
В уравнении (1.5) первое слагаемое представляет собой функцию только 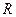 , а второе слагаемое- функцию только
, а второе слагаемое- функцию только 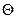 . Сумма двух функций, из которых одна зависит от
. Сумма двух функций, из которых одна зависит от 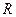 , а другая от
, а другая от 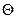 , равна нулю для бесчисленного множества пар значений
, равна нулю для бесчисленного множества пар значений 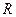 и
и 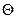 . Это возможно тогда, когда каждая из данных функций равна нулю:
. Это возможно тогда, когда каждая из данных функций равна нулю:
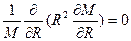 ;
; 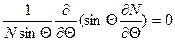 (1.5')
(1.5')
или
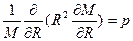 ;
; 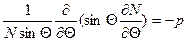 (1.5'')
(1.5'')
Так как в (1.5') 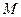 зависит только от
зависит только от 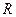 , а
, а 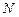 от
от 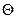 , то от частных производных можна перейти к полным:
, то от частных производных можна перейти к полным:
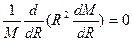 ;
; 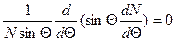
Решаем эти уравнения:
1) 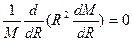
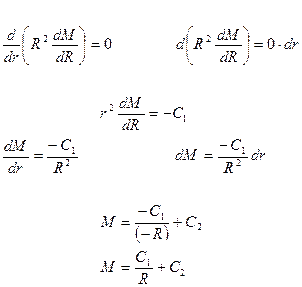
2) 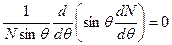
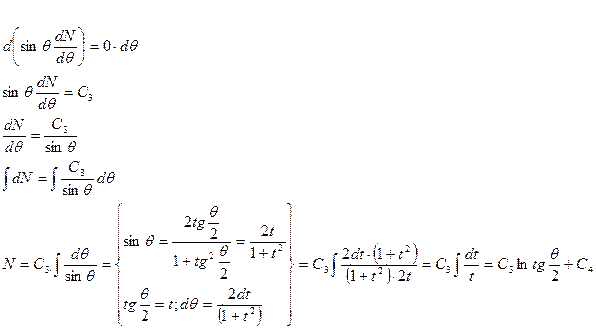
Покажем, что 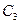 =0, так как только в этом случае в решении отсутствует слагаемое
=0, так как только в этом случае в решении отсутствует слагаемое 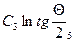 . Потенциал- это непрерывная функция и на конечном отрезке он не может измениться на бесконечно большую величину. Таким образом, потенциал точек оси z вблизи шара не может быть равен бесконечности. Следовательно
. Потенциал- это непрерывная функция и на конечном отрезке он не может измениться на бесконечно большую величину. Таким образом, потенциал точек оси z вблизи шара не может быть равен бесконечности. Следовательно 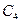 должно равняться нулю.
должно равняться нулю.
Тогда частное решение для 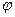 , вытекающее с (1.5') :
, вытекающее с (1.5') :
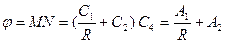 , где
, где 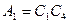 ,
, 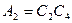 (1.6)
(1.6)
Найдем решение уравнений (1.5''):
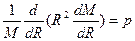
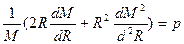
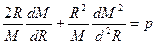 ;
; 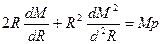
Применим подстановку Эйлера: 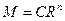
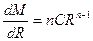 ;
; 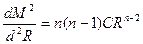
Подставим производные в уравнение:
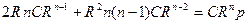
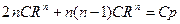
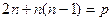 ;
; 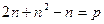 ;
; 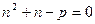
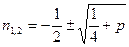 (1.7)
(1.7)
Значение 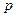 найдем при интегрировании второго уравнения (1.5''):
найдем при интегрировании второго уравнения (1.5''):
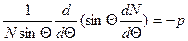
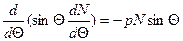
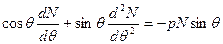
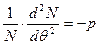
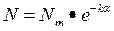
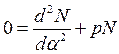
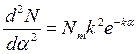
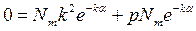
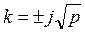
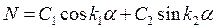
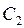 =0, потому как j - функция парная, т.е.
=0, потому как j - функция парная, т.е. 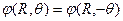 тогда N(ka)=Bcos(ka). Если принять, что потенциал на оси у равен 0
тогда N(ka)=Bcos(ka). Если принять, что потенциал на оси у равен 0 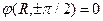 то
то 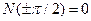 , а соответственно, k=1. При k>1 нулевая потенциальная линия будет наклонена к оси у, что не соответствует изучаемому полю (потенциал равен нулю по оси z).
, а соответственно, k=1. При k>1 нулевая потенциальная линия будет наклонена к оси у, что не соответствует изучаемому полю (потенциал равен нулю по оси z).
Таким образом решение уравнения можно записать в виде 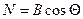 , убедимся в этом путем подстановки, найдем при этом
, убедимся в этом путем подстановки, найдем при этом 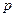 :
:
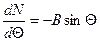 ;
; 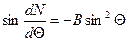 ;
;
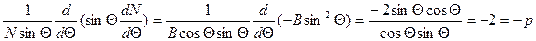
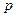 =2
=2
Подставим 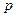 =2 в (1.7):
=2 в (1.7):
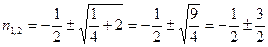
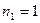 ,
, 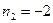
Совместное решение уравнений (1.5'') дает следующее выражение для 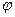 :
:
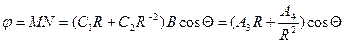 (1.8)
(1.8)
где 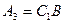 ,
, 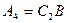
Полное решение:
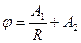
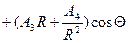
Полное решение подходит и для данной задачи. Таким образом потенциал внутренней области запишем:
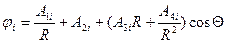 (1.9)
(1.9)
Для внешней области:
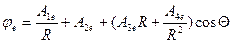 (1.10)
(1.10)
Задача сводится к нахождению постоянных интегрирования. Для их нахождения необходимо учесть граничные условия на поверхности, а так же поведение потенциала на бесконечности.
Потенциал на бесконечности определим так [1.565]:
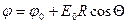 (1.11)
(1.11)
Сопоставим (1.11) с (1.10), получим:
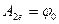 ;
; 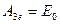
Потенциал в поле точечного заряда изменяется обратно пропорционально 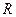 . Поэтому
. Поэтому 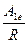 есть составляющая потенциала от суммарного заряда шара, рассматриваемого как точечный заряд. Суммарный заряд шара равен нулю, тогда
есть составляющая потенциала от суммарного заряда шара, рассматриваемого как точечный заряд. Суммарный заряд шара равен нулю, тогда 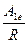 =0. Выражение для
=0. Выражение для 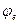 записываем:
записываем:
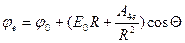 (1.10')
(1.10')
Рассмотрим выражение потенциала 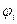 для внутренней области. Оно должно давать конечное значение для всех точек внутри шара. Это возможно при
для внутренней области. Оно должно давать конечное значение для всех точек внутри шара. Это возможно при 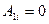 и
и 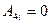 . Постоянная
. Постоянная 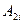 равна аналогичной постоянной
равна аналогичной постоянной 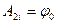 для внешней области. Выражение для внутренней области:
для внешней области. Выражение для внутренней области:
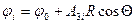 (1.9')
(1.9')
Константы 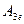 и
и 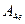 найдем из граничных условий.
найдем из граничных условий.
Из равенства потенциалов 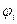 и
и 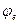 , при
, при 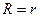 следует:
следует:
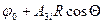
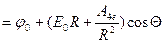
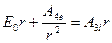 (1.12)
(1.12)
Из равенства 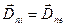 на границе следует:
на границе следует:
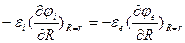
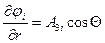 ;
; 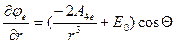
Подставив и сократив на 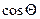 получаем:
получаем:
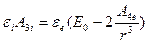 (1.13)
(1.13)
Получаем систему уравнений (1.12) и (1.13):
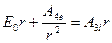
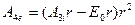
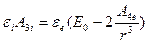
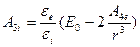
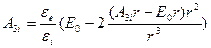
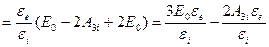
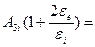
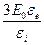
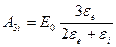 ;
;
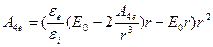
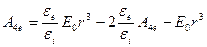
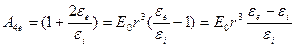
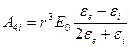
Тогда потенциал внутренней области переписываем в виде:
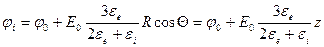 (1.9'')
(1.9'')
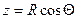
Для внешней области:
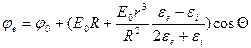 (1.10'')
(1.10'')
Найдем напряженности поля в шаре и вне шара:
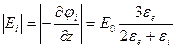 (1.14)
(1.14)
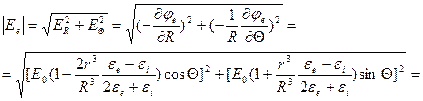
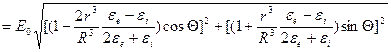
Вектор электрической индукции за пределами шара определяется формулой:
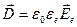
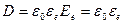
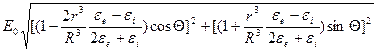
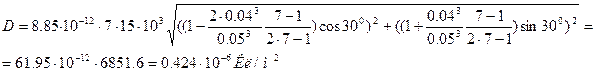
Проверим размерность полученного значения:
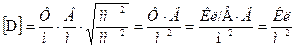
Составляем блок-схему и программу для расчета и построения эквипотенциальных линий. Текст программы и блок-схема приведены в приложении А. С помощью программы получен следующий результат(рис 1.).
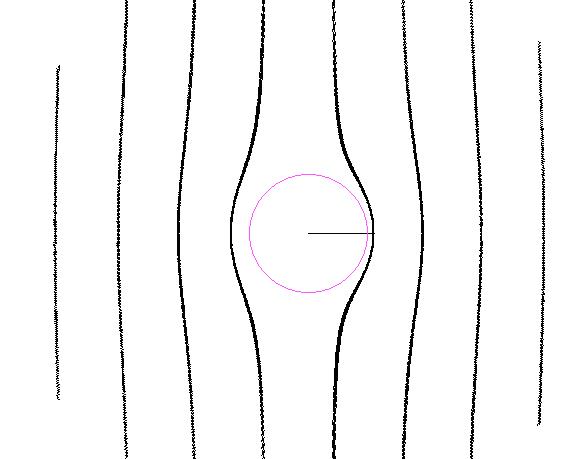
Рисунок 1. – Изображение эквипотенциальных линий электрического поля.
