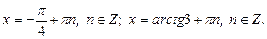Задания для самостоятельного решения
I уровень
1.1. Проверьте, справедливо ли равенство:
1) 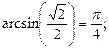 2)
2) 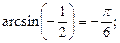
3) 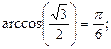 4)
4) 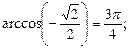
5) 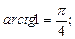 6)
6) 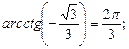
7) 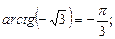 8)
8) 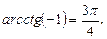
1.2. Вычислите:
1) 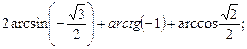
2) 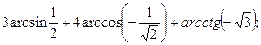
3) 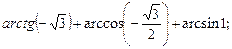
4) 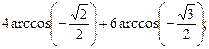
5) 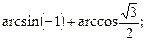
6) 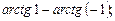
7) 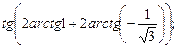
8) 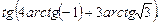
1.3. Решите уравнение:
1) 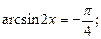 2)
2) 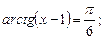
3) 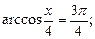 4)
4) 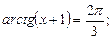
5) 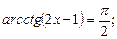 6)
6) 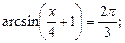
7) 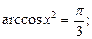 8)
8) 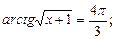
9) 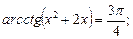 10)
10) 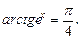
1.4. Найдите область определения функции:
1) 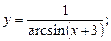 2)
2) 
1.5. Постройте график функции:
1) 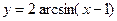 ; 2)
; 2) 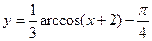 ;
;
3) 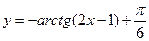 ; 4)
; 4) 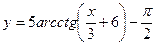
1.6. Постройте на единичной окружности угол 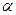 такой, что:
такой, что:
1) 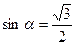 ; 2)
; 2) 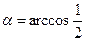 ;
;
3) 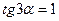 ; 4)
; 4) 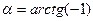 ;
;
5) 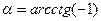 ; 6)
; 6) 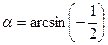 .
.
II уровень
2.1. Вычислите:
1) 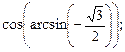 2)
2) 
3) 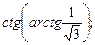 4)
4) 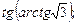
5) 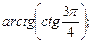 6)
6) 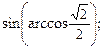
7) 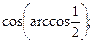 8)
8) 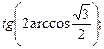
9) 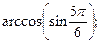 10)
10) 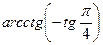 ;
;
11) 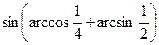 .
.
2.2. Сравните числа:
1)  2)
2) 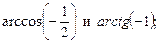
3) 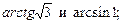 4)
4) 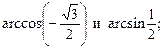
5) 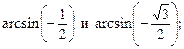 6)
6) 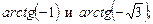
7) 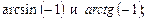 8)
8) 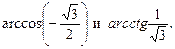
2.3. Решите уравнение:
1) 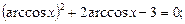
2) 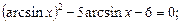
3) 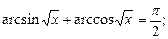
4) 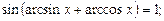
5) 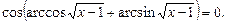
2.4. Найдите область определения функции:
1) 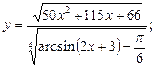 2)
2) 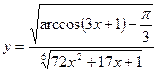 ;
;
3) 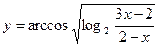 ;
;
4) 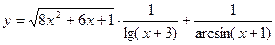 ;
;
5) 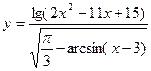 .
.
2.5. Постройте график функции:
1) 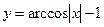 ;
;
2)  ;
;
3) 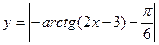 ;
;
4) 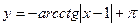 .
.
2.6. Постройте на единичной окружности угол 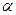 такой, что:
такой, что:
1) 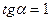 ; 2)
; 2) 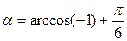 ;
;
3) 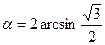 ; 4)
; 4) 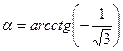 ;
;
5) 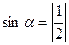 .
.
III уровень
3.1. Вычислите:
1) 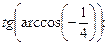 2)
2) 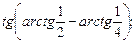
3) 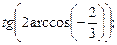 4)
4) 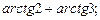
5) 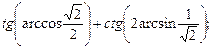
6) 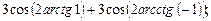
7) 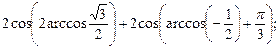
8) 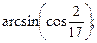
10) 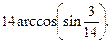
3.2. Решите уравнения:
1) 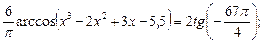
2) 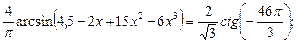
3) 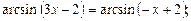
4) 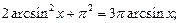
5) 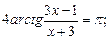
6) 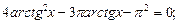
7) 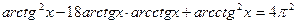 ;
;
8) 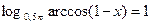 ;
;
9) 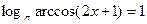 .
.
3.3. Решите неравенство:
1) 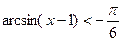 ;
;
2)  ;
;
3) 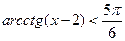 ;
;
4) 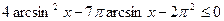 ;
;
5) 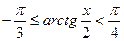 .
.
3.4. Известно, что числа 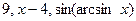 являются тремя последовательными членами геометрической прогрессии. Найдите
являются тремя последовательными членами геометрической прогрессии. Найдите 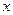 .
.
3.5. Постройте график функции:
1) 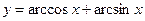 ,
,  ;
;
2) 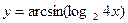 ;
;
3) 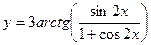 ;
;
4) 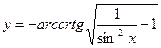 .
.
3.6. Постройте на единичной окружности угол 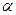 такой, что:
такой, что:
1) 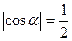 ; 2)
; 2) 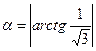 ;
;
3) 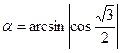 ; 4)
; 4) 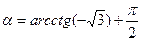 ;
;
5) 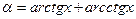 .
.
Тригонометрические уравнения
Приведем основные типы уравнений.
I. Простейшие тригонометрические уравнения
Уравнение
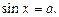 (18)
(18)
Если 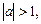 то уравнение (18) решений не имеет, так как
то уравнение (18) решений не имеет, так как 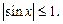
Если 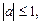 то уравнение имеет решение, которое находится по формуле:
то уравнение имеет решение, которое находится по формуле:
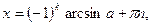
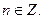 (19)
(19)
Частные случаи уравнения (18):
уравнение 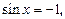 решение
решение 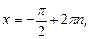
 ;
;
уравнение 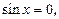 решение
решение 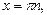
 ;
;
уравнение 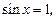 решение
решение 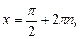
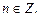
Уравнение
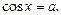 (20)
(20)
Если 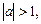 то уравнение решений не имеет, так как
то уравнение решений не имеет, так как 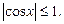
Если 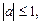 то уравнение (20) имеет решение, которое находится по формуле:
то уравнение (20) имеет решение, которое находится по формуле:
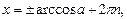
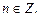 (21)
(21)
Частные случаи уравнения (20):
уравнение  решение
решение 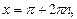
 ;
;
уравнение 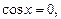 решение
решение 
 ;
;
уравнение 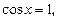 решение
решение 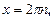
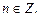
Уравнение

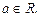 . (22)
. (22)
Решение уравнения (22) находят по формуле:
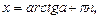
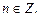 (23)
(23)
Уравнение
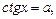
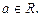 (24)
(24)
Решение уравнения (24) находят по формуле:
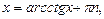
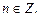 (25)
(25)
Пример 1.Решить уравнение
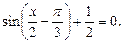
Решение.Запишем уравнение в виде
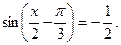
и воспользуемся формулой (19):
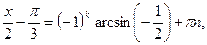
 .
.
Используем нечетность функции 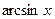 :
:
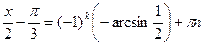 ,
,  ,
,
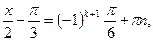
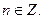
Из последнего равенства находим:
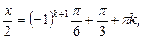
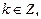
что приводит к ответу
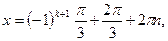
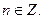
Пример 2.Решить уравнение
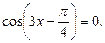
Решение.Воспользуемся частным случаем решения уравнения типа (20):
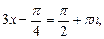
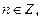
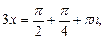
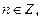
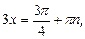
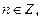
приходим к ответу
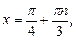
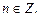
Пример 3. Решить уравнение
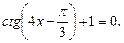
Решение. Найдем решение по формуле (25):
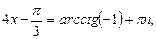
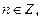
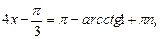
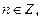
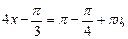
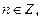
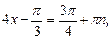
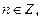
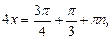
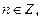
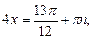
 .
.
Получаем ответ: 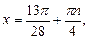
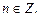
II. Уравнения, решаемые разложением на множители
Пример 4. Решить уравнение
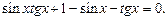
Решение.ОДЗ: 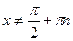 ,
,  .
.
Преобразуем уравнение следующим образом:
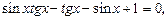
откуда
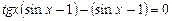
или
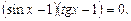
Решаем совокупность:
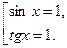
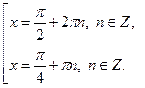
Однако решение 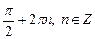 не удовлетворяет ОДЗ исходного уравнения. Поэтому получаем ответ:
не удовлетворяет ОДЗ исходного уравнения. Поэтому получаем ответ:
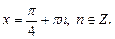
Пример 5. Решить уравнение
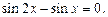
Решение. Используя формулу 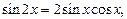 запишем уравнение в виде:
запишем уравнение в виде:
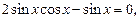
откуда
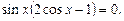
Решаем совокупность:
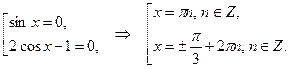
Получаем ответ:
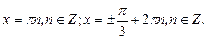
Пример 6. Решить уравнение
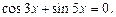
Решение. Используем формулу приведения и запишем уравнение в виде:
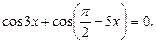
Преобразуем по формуле суммы косинусов:
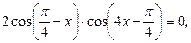
откуда получаем совокупность:
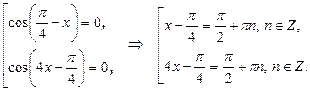
Приходим к ответу:
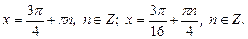
III. Уравнения, решаемые с помощью формул
Преобразования произведения тригонометрических
Функций в сумму
Пример 7.Решить уравнение
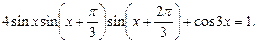
Решение.Преобразуем произведение 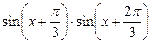 в сумму, получим
в сумму, получим
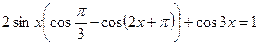 ;
;
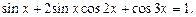
Преобразуем в сумму произведение 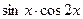 :
:
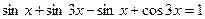 ,
,
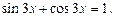
Используем формулу приведения и представим последнее уравнение в виде
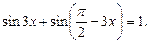
Преобразуем полученную сумму синусов в произведение:
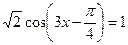 .
.
Получаем уравнение
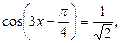
которое решаем по формуле (21):
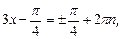
 .
.
Получаем ответ
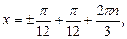
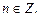
IV. Уравнения, решаемые с помощью замены переменной
Пример 8.Решить уравнение
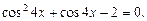
Решение.Данное уравнение является квадратным относительно 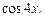 Заменяем
Заменяем 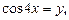 получим уравнение
получим уравнение 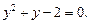 Его корни
Его корни 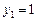 и
и 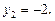 Таким образом, решение исходного уравнения свелось к решению совокупности простейших уравнений:
Таким образом, решение исходного уравнения свелось к решению совокупности простейших уравнений:
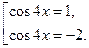
Уравнение 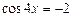 корней не имеет, т.е.
корней не имеет, т.е. 
Решением второго является
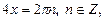
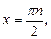
 .
.
Получаем ответ: 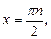
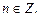
Пример 9.Решить уравнение
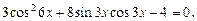
Решение.Используем тождество 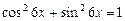 и формулу
и формулу 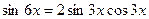 . Уравнение сводится к виду:
. Уравнение сводится к виду:
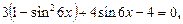
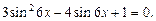
Мы получили квадратное уравнение относительно 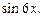 Заменяем
Заменяем 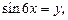 получим уравнение
получим уравнение 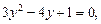 откуда
откуда 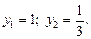
Приходим к совокупности простейших уравнений:
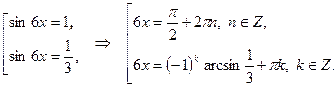
Получаем ответ:
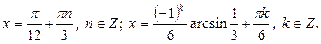
Пример 10.Найти сумму корней уравнения
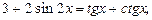 если
если 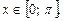
Решение.ОДЗ: 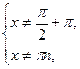 поскольку
поскольку 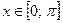 ,
, 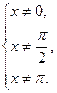
Упростим исходное уравнение:
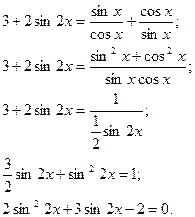
Получили квадратное уравнение относительно 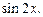 Сделав замену
Сделав замену 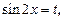 где
где 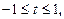 имеем уравнение
имеем уравнение 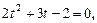 откуда
откуда 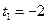 или
или 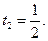
Вернувшись к прежней неизвестной, получим совокупность уравнений
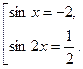
Первое уравнение не имеет решения. Решаем второе:
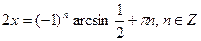 ;
;
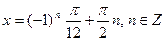 .
.
Придаем 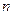 значение
значение 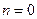 ; получаем
; получаем
 ;
;
при 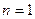 имеем
имеем 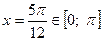 .
.
Нетрудно убедиться, что при всех других значениях n корни не попадут на отрезок 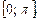 Значит сумма корней, принадлежащих отрезку
Значит сумма корней, принадлежащих отрезку 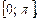 равна
равна
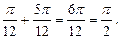
Ответ: 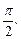
V. Однородные уравнения
Однородным тригонометрическим уравнениями n-й степени относительно 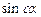 и
и 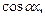
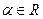 , называется уравнение вида
, называется уравнение вида
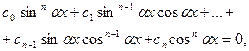 (26)
(26)
где 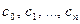 – действительные числа,
– действительные числа, 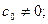
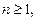
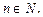
В уравнении (26) 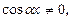 так как при
так как при 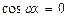 исходное уравнение примет вид:
исходное уравнение примет вид: 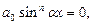 откуда
откуда 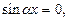 что невозможно, поскольку
что невозможно, поскольку 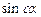 и
и 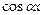 не могут одновременно равняться нулю.
не могут одновременно равняться нулю.
Разделив исходное уравнение на 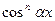 получим:
получим:
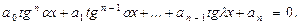
С помощью замены 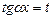 имеем алгебраическое уравнение
имеем алгебраическое уравнение
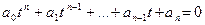 ,
,
которое решаем и возвращаемся к старой переменной.
Пример 11.Решить уравнение
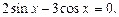
Решение.Разделив уравнение на 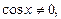 получим
получим 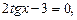 откуда
откуда 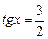 и
и 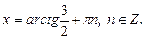
Ответ: 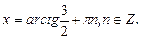
Пример 12. Решить уравнение
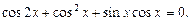
Решение.Используя формулу 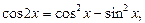 приведем данное уравнение к однородному:
приведем данное уравнение к однородному:


Разделим почленно на 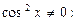
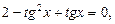
откуда
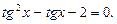
Введем замену 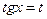 и получим уравнение
и получим уравнение  корнями которого будут
корнями которого будут 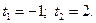
После чего перейдем к решению совокупности простейших уравнений:
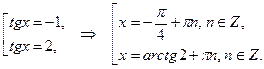
Получили ответ:
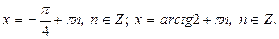
VI. Неоднородные уравнения 2-й степени
Неоднородным тригонометрическим уравнением 2-й степени называется уравнение вида
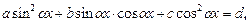
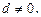 (27)
(27)
Используя основное тригонометрическое тождество приводим уравнение к однородному
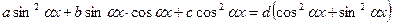 ,
,
которое решаем далее как уравнение типа (26).
Пример 13.Решить уравнение
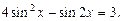
Решение.Используя формулы 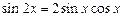 и
и
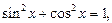 преобразуем данное уравнение к однородному:
преобразуем данное уравнение к однородному:
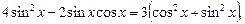
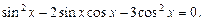
Разделим на 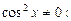
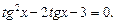
Введем замену 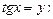
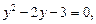 откуда
откуда 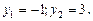
Решим совокупность уравнений:
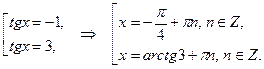
Получили ответ: