Дослідження резонансних явищ
У ПОСЛІДОВНОМУ КОЛИВАЛЬНОМУ КОНТУРІ
Мета роботи –дослідити характеристики послідовного коливального контуру при різних характерах повного опору кола. Побудувати векторні діаграми напруг. Дослідити резонанс напруг та визначити резонансні характеристики струму та напруги на реактивних елементах послідовного контуру.
Теоретичні відомості
Послідовним коливальним контуром називають коло, що складається з послідовного з’єднання активного опору, котушки, конденсатора і джерела живлення (рис. 5.1).

Рис. 5.1. Послідовний коливальний контур
Опір  в радіотехнічних контурах являє собою власні опори радіодеталей: котушки і конденсатора. Інакше кажучи – це неминучий опір, який називається іноді опором втрат контуру.
в радіотехнічних контурах являє собою власні опори радіодеталей: котушки і конденсатора. Інакше кажучи – це неминучий опір, який називається іноді опором втрат контуру.
Струм в послідовному колі визначається як:

де  – реактивний опір кола.
– реактивний опір кола.
Резонанс в колі наступає, коли  , тобто при частоті
, тобто при частоті
 ,
,
звідки частота  і період
і період  відповідно будуть дорівнювати:
відповідно будуть дорівнювати:
 .
.
Реактивні опори при резонансі дорівнюють один одному

і називають характеристичними опорами контуру. Відношення характеристичного опору до опору втрат 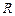 називаються добротністю контуру
називаються добротністю контуру  :
:
 .
.
Так як  , то
, то  для радіотехнічних контурів значення добротності
для радіотехнічних контурів значення добротності  . Величину, обернену добротності, називають затуханням
. Величину, обернену добротності, називають затуханням
 .
.
Величини  послідовного коливального контуру (рис. 5.1) називають первинними, а величини
послідовного коливального контуру (рис. 5.1) називають первинними, а величини  отримали назву вторинних параметрів контуру.
отримали назву вторинних параметрів контуру.
Коли в послідовному контурі  , то коло веде себе так, ніби реактивні опори в колі відсутні і струм обмежується тільки активним опором. Тоді струм у контурі при резонансі:
, то коло веде себе так, ніби реактивні опори в колі відсутні і струм обмежується тільки активним опором. Тоді струм у контурі при резонансі:
 .
.
Величина  є найбільшим можливим значенням струму.
є найбільшим можливим значенням струму.
Коло в даному випадку веде себе як резистивне, але на реактивних елементах можуть виникати напруги на багато разів перевищуючи напругу на вході кола,  .
.
Напруга на реактивних елементах контуру:

У зв’язку з можливістю виникнення напруг на індуктивності і ємності, які у десятки і сотні разів можуть перевищувати напругу вхідного сигналу, вид резонансу отримав назву резонанс напруг.
На рис. 5.2 наведені частотні характеристики вхідних опорів послідовного коливального контуру і його фазочастотна характеристика. Характеристика отримана шляхом геометричного підсумовування кривих  та
та  .
.
Фазочастотна характеристика  побудована на основі рівняння
побудована на основі рівняння
 ,
,
яке отримано з трикутників опорів (рис. 3.5, а, б).
Складемо рівняння амплітудно-частотної характеристики для струму.
 ,
,
де  – найбільше для даного кола значення струму, яке має місце при резонансі, коли
– найбільше для даного кола значення струму, яке має місце при резонансі, коли  :
:

Тоді


Рис. 5.2. Частотні характеристики вхідних опорів та фазочастотна характеристика послідовного контуру
Зручно користуватися вираженням струму в відносних одиницях, яке називають нормованим струмом:

Ми отримали рівняння амплітудно-частотної характеристики струму, в якій враховується добротність контуру.
Аналогічно можна виразити фазочастотну характеристику в якій також враховується добротність контуру.

На рис. 5.3 наведений приблизний вид амплітудно-частотних характеристик для контурів різних добротностей.

Рис. 5.3. Амплітудно-частотні характеристики
для контурів різних добротностей
Як видно з рис. 5.3 чим більша добротність контуру, тим більш гострою і вузькою стає характеристика, тим більша вибірковість контуру. Величина

є функцією частоти і перетворюється в нуль, коли  , тобто коли частота власних коливань контуру
, тобто коли частота власних коливань контуру 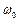 співпадає з частотою сигналу джерела. Відхилення частоти джерела в будь-який бік від резонансної
співпадає з частотою сигналу джерела. Відхилення частоти джерела в будь-який бік від резонансної 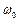 веде до зростання величини а. Коли
веде до зростання величини а. Коли  , то кажуть що контур налагоджений. Коли
, то кажуть що контур налагоджений. Коли  , тоді контур розлагоджений. У міру розстройки контуру зручно судити з величини
, тоді контур розлагоджений. У міру розстройки контуру зручно судити з величини  , яку і називають узагальненою розстройкою. Контур можна налагодити, змінюючи частоту джерела чи параметри самого контуру.
, яку і називають узагальненою розстройкою. Контур можна налагодити, змінюючи частоту джерела чи параметри самого контуру.
Ступінь розстройки можна також характеризувати двома іншими величинами:
 – абсолютна розстройка;
– абсолютна розстройка;
 – відносна розстройка.
– відносна розстройка.
Для невеликих розстроєк, коли  , можна отримати приблизне значення узагальненої розстройки
, можна отримати приблизне значення узагальненої розстройки

На рис. 5.4 наведені фазочастотні характеристики послідовних контурів різних добротностей.

Рис. 5.4. Фазочастотні характеристики для послідовних коливальних контурів різних добротностей
Оскільки фазочастотна характеристика  визначає фазовий кут вхідного опору контуру, то при частотах менше резонансної коло має ємнісний характер
визначає фазовий кут вхідного опору контуру, то при частотах менше резонансної коло має ємнісний характер  <0. При резонансній частоті
<0. При резонансній частоті  опір контуру стає чисто активним. На частотах більших від резонансної коло має індуктивний характер
опір контуру стає чисто активним. На частотах більших від резонансної коло має індуктивний характер  .
.
Порядок виконання роботи
1. Накреслити схему послідовного коливального контуру (рис. 5.5) з параметрами відповідно до варіанта (табл. 5.1)

Рис. 5.5. Схема послідовного коливального контуру
Таблиця 5.1
| Номер варіанта | Резонансна частота 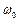 , рад/с , рад/с | Амплітуда ЕРС  , В , В | Опір 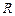 , Ом , Ом | Індуктивність 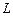 , мГн , мГн | Ємність 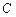 , мкФ , мкФ |
| 0,25 | |||||
| 0,02 | |||||
| 0,4 | |||||
| 0,5 | |||||
| 1 | 2 | 3 | 4 | 5 | 6 |
| 0,05 | |||||
| 0,4 | |||||
| 0,05 | |||||
| 0,25 | |||||
| 0,01 | |||||
| 0,025 |
2. Розрахувати значення характеристичного опору  , добротність контуру
, добротність контуру  , затухання
, затухання  .
.
3. Розрахувати діючі значення струму і напруг на реактивних елементах при резонансі.
4. Побудувати графіки резонансних характеристик струму послідовного контуру для різних значень добротності контуру  .
.
5. Побудувати графіки резонансних характеристик напруги чи індуктивності для різних значень добротності контуру
 :
:

6. Побудувати графіки резонансних характеристик на ємності для різних значень добротності контуру  .
.

7. Побудувати графіки залежності повного опору послідовного коливального контуру для різних значень добротності контуру  .
.

8. Побудувати графіки залежності зсуву фаз послідовного коливального контуру для різних значень добротності контуру  .
.
 .
.
9. Здійснити математичне моделювання послідовного коливального контуру (рис. 5.6).

Рис. 5.6. Математичне моделювання послідовного коливального контуру
Виміряти значення струму та напруг на всіх елементах контуру для різних значень добротності контуру. Результати вимірювання занести до табл. 5.2 і порівняти з результатами розрахунку.
Таблиця 5.2
| І, A |  , В , В |  , В , В |  , В , В |  , град , град | |
| Результати обчислення | |||||
| Результати математичного моделювання | |||||
| Похибка |
10. За допомогою віртуального осцилографа (рис. 5.7) виміряти фазовий зсув між струмом у контурі  та ЕРС
та ЕРС  . Результати вимірювання порівняти з результатами розрахунку.
. Результати вимірювання порівняти з результатами розрахунку.

Рис. 4.6. Миттєві значення струмів до розгалуження
11. Побудувати векторну діаграму напруг при резонансі.
Зміст звіту
Звіт повинен містити:
1. Мету і порядок виконання роботи;
2. Результати розрахунку характеристичного опору  , добротності контуру
, добротності контуру  , затухання
, затухання  ;
;
3. Результати розрахунку значення струму в колі і напруг на елементах кола при резонансі;
4. Графіки залежностей:  для різних значень добротності контуру;
для різних значень добротності контуру;
5. Результати математичного моделювання послідовного коливального контуру;
6. Осцилограми результатів математичного моделювання;
7. Векторну діаграму напруг при резонансі;
8. Короткі висновки за результатами роботи.
Контрольні питання
1. В якому колі виникає резонанс напруг?
2. Напишіть умови наступу резонансу в послідовному коливальному контурі.
3. Які параметри первинні і які вторинні для послідовного коливального контуру?
4. Які частотні характеристики послідовного контуру ви могли б навести?
5. Чому дорівнює повний опір при резонансі?
Лабораторна робота 6
