Бесконечно малые функции и их свойства
Определение
Функция 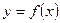 называется бесконечно малой в точке
называется бесконечно малой в точке 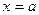 , если ее предел в этой точке равен нулю:
, если ее предел в этой точке равен нулю:  .
.
Аналогично определяются бесконечно малые при 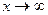 ,
, 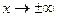 и др.
и др.
Теорема
Если функция 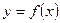 имеет предел в точке
имеет предел в точке 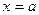 , равный A, то функция
, равный A, то функция  является бесконечно малой в точке
является бесконечно малой в точке 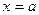 .
.
Свойства бесконечно малых функций
1. Алгебраическая сумма конечного числа бесконечно малых величин есть величина бесконечно малая.
2. Произведение бесконечно малой величины на ограниченную функцию есть величина бесконечно малая.
3. Частное от деления бесконечно малой величины на функцию, предел которой отличен от нуля, есть величина бесконечно малая.
Бесконечно большие функции и их свойства
Определение
Функция  называется бесконечно большой в точке
называется бесконечно большой в точке  , если для любой, сходящейся к
, если для любой, сходящейся к 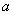 последовательности значений аргумента
последовательности значений аргумента 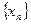 , соответствующая последовательность значений функции
, соответствующая последовательность значений функции 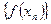 является бесконечно большой последовательностью.
является бесконечно большой последовательностью.
В этом случае пишут:  .
.
Аналогично определяются бесконечно большие функции при 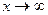 ,
, 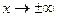 и др. Отметим, что между бесконечно малыми и бесконечно большими функциями существует такая же связь, что и между бесконечно малыми и бесконечно большими последовательностями.
и др. Отметим, что между бесконечно малыми и бесконечно большими функциями существует такая же связь, что и между бесконечно малыми и бесконечно большими последовательностями.
Теорема
Если  – бесконечно малая функция при
– бесконечно малая функция при  , то
, то  – бесконечно большая функция при
– бесконечно большая функция при  и наоборот.
и наоборот.
Свойства бесконечно больших функций
1. Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.
2. Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.
3. Частное от деления бесконечно большой величины на функцию, имеющую предел, есть величина бесконечно большая.
Основные теоремы о пределах. Признаки существования предела
Теорема
Функция не может иметь более одного предела.
Теорема
Пусть заданные на одном и том же множестве функции 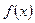 и
и 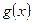 имеют в точке
имеют в точке 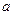 пределы соответственно
пределы соответственно 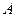 и
и  . Тогда функции
. Тогда функции
 ,
, 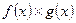 и
и 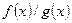 (при
(при  )
)
имеют в точке а пределы, равные соответственно:
 ,
,  и
и  .
.
Признаки существования предела
1. Если числовая последовательность 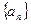 монотонна и ограничена, то она имеет предел.
монотонна и ограничена, то она имеет предел.
2. Если в некоторой окрестности точки x0 (или при достаточно больших значениях x) функция f(x) заключена между двумя функциями j(x) и y(x), имеющими одинаковый предел A при  (или
(или 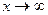 ), то функция f(x) имеет тот же предел A.
), то функция f(x) имеет тот же предел A.
Замечательные пределы.
Первый замечательный предел
Теорема
Предел функции  в точке
в точке 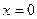 существует и равен единице, т.е.
существует и равен единице, т.е.
 | (4.6.1) |
Предел (4.6.1) называется первым замечательным пределом и применяется при вычислении ряда других пределов. Рассмотрим несколько примеров на применение предела (4.6.1).
Пример
Найти предел функции при
при  .
.
Решение
Преобразуем данную дробь так, чтобы в знаменателе был аргумент синуса; только тогда можно будет применить первый замечательный предел, поскольку при  пределом
пределом  также является нуль:
также является нуль:

Пример
Найти  .
.
Решение
Первый замечательный предел здесь непосредственно применить нельзя, так как при  знаменатель дроби стремится к нулю. Для решения задачи необходимо преобразовать данную дробь:
знаменатель дроби стремится к нулю. Для решения задачи необходимо преобразовать данную дробь:

Второй замечательный предел
Теорема
Предел функции  при
при 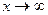 существует и равен
существует и равен  , т.е.
, т.е.
 . . | (4.6.2) |
Предел (4.6.2) называется вторым замечательным пределом и применяется при вычислении ряда других пределов. e = 2.718281…
Пример
Найти  .
.
Решение
Выполним здесь замену переменной, полагая  . Тогда
. Тогда  при
при  , т.е.
, т.е.

Пример
Найти 
Решение
Преобразуем дробь под знаком предела:

Пример
Найти  .
.
Решение
Сделаем замену  . Тогда
. Тогда

Пример
Найти  .
.
Решение
Сделаем замену  . Тогда
. Тогда

