Расчет постоянных интегрирования

Записать выражения для искомого тока (напряжения) с учетом результатов, полученных на 1 и 2 этапах (значения принужденной составляющей и корней характеристического уравнения) и продифференцировать его последовательно n-1 раз. Подставить в эти n выражений t = 0 и значения найденных на 3 этапе начальных условий. В итоге получим систему уравнений относительно неизвестных постоянных интегрирования, позволяющую рассчитать их значение.

Задача 1

В схеме рис.6 ключ коммутируется из положения 1 в положение 2. До коммутации в схеме установившейся режим. Параметры схемы: R₁=100 Ом, R₂=300 Ом, R₃=100 Ом, R₄=200 Ом, L=25мГн, C=0,1 мкФ, Е=200 В, J=0,4 А. Рассчитать 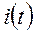после коммутации ключа.

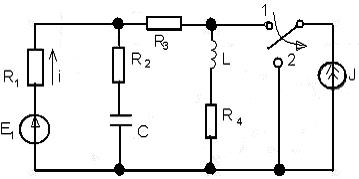
Рис. 6

Проведем расчет тока 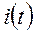классическим методом в соответствии с методикой, изложенной в теоретических сведениях.

1) Расчет принужденной составляющей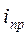

В схеме действуют постоянные источники, поэтому через некоторое время после коммутации в схеме будет установившийся режим постоянного тока (УРПТ). Определим 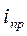из анализа УРПТ после коммутации. Расчетная схема (схема установившегося режима постоянного тока после коммутации ключа) представлена на рис.7

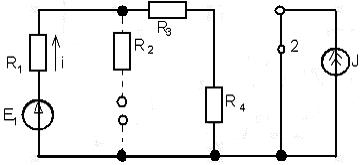
Рис. 7

Схема имеет такой вид, так как в УРПТ ток через емкость и напряжение на индуктивности равны нулю. Это утверждение отражают на эквивалентной схеме следующими заменами:

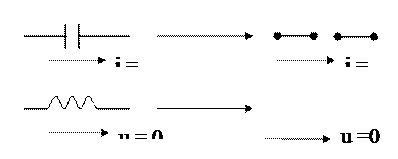
Тогда по ЗКН для схемы (рис.7) имеем

.

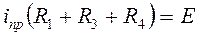
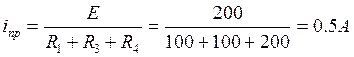2) Составление характеристического уравнения и определение его корней.

Поскольку требуется рассчитать ток только в одной ветви, то для получения характеристического уравнения воспользуемся методом входного сопротивления. Для этого составим схему свободной составляющей и сделаем разрыв в той ветви, относительно тока которой требуется записать характеристическое уравнение (рис.8). Запишем выражение для входного (эквивалентного) сопротивления относительно зажимов разрыва.

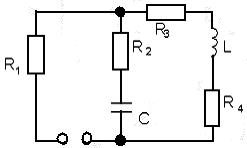
Рис. 8

.

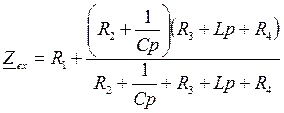Приравняем выражение для 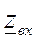нулю

.

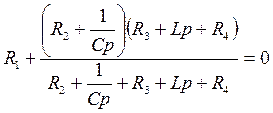Это уравнение является характеристическим относительно тока .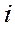

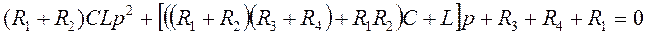Подставив значение параметров, и проведя необходимые расчеты, получим

.

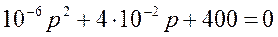Определим корни этого уравнения

.

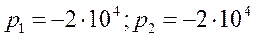Так как p₁=p₂, т.е. корни кратные, то решение записывают в виде

,

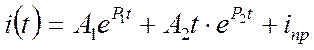A₁ и A₂ – постоянные интегрирования.

3) Расчет начальных условий

а) Расчет независимых начальных услови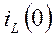й и 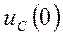. Рассмотрим режим работы схемы до коммутации. В схеме с постоянными источниками до коммутации установившийся режим, т.е. установившийся режим постоянного тока. В УРПТ коммутации схема имеет вид (рис.9)

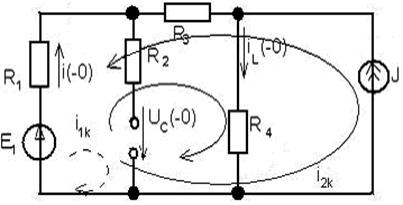
Рис. 9

Определим 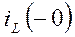методом контурных токов. Для указанных контуров (рис.9) будем иметь

.

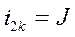
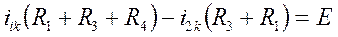Учитывая, что 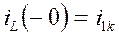получим

.

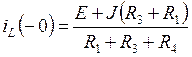Или с учетом параметров схемы

.

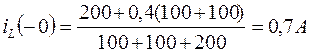
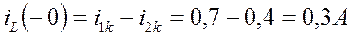Напряжение 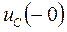рассчитаем по ЗКН, записанному для пунктирного контура (рис 9)

.

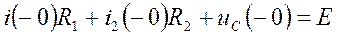Учитывая, что 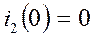(в ветви разрыв)

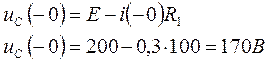
В соответствии с законами коммутации искомые независимые начальные условия

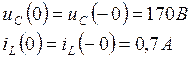
б) Расчет зависимых начальных условий

Выражение тока 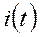содержит две постоянные интегрирования, для определения этих постоянных интегрирования необходимо иметь значения двух начальных условий, а именно, 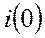и .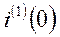

Зависимые начальные условия рассчитываются по схеме после коммутации (риc.10)

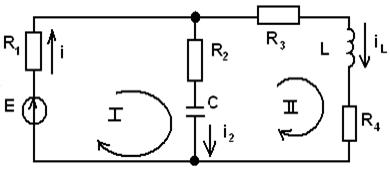
Рис. 10

Запишем для схемы (рис.10) полную системы независимых уравнений по ЗК

1. .

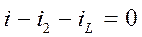2. .

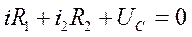3. .

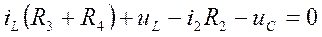Выразим 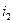из первого уравнения

.

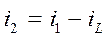И подставим во второе

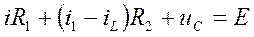
или

.

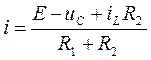С учетом этого результата, записанную выше систему уравнений можно представить в следующем виде

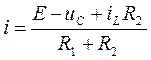(1.1)

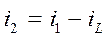(1.2)

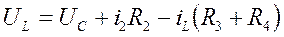. (1.3)

Эта система уравнений (также как и предыдущая) справедлива для любого 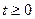, и используется для расчета начальных условий.

Рассмотрим уравнения 1.1 - 1.3 при 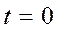и определим .

.

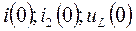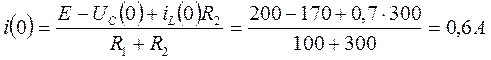
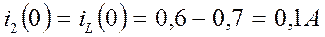
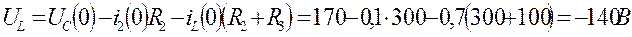Определим 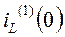и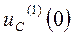

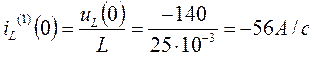
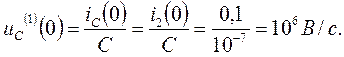
Продифференцируем уравнение (1.1)

.

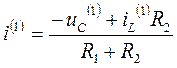И рассмотрим при t=0

.

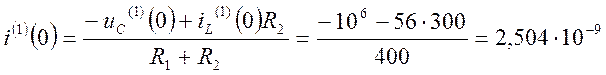Таким образом необходимые начальные условия 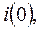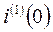определены.

4) Расчет постоянных интегрирования

Искомый ток 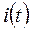в соответствии с результатами, полученными на I и II этапах расчета

.

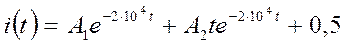Продифференцируем это выражение

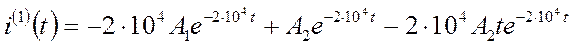
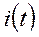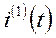И подставим в выражение для и t=0

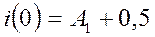
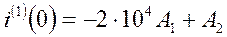
Тогда

.

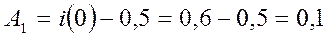
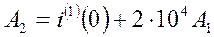Задача 2

Дано: R₁=R₂=10 Ом, R₃=20 Ом, С=1000 мкФ,L=100 мГн. Е=320 Ом. До коммутации в схеме установившейся режим.

Определить: закон изменения тока i_C(t) в схеме рис.11 после коммутации ключа.

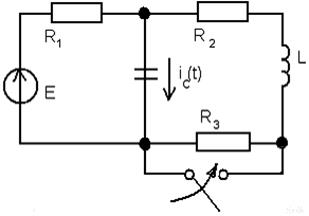
Рис. 11

Решение:

1. Определение принужденной составляющей.

В схеме действует источник постоянной эдс Е, поэтому рассчитаем i_спр по схеме установившегося режима постоянного тока после коммутации (рис.12)

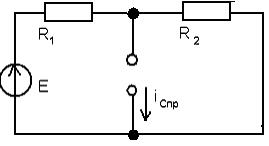
Рис. 12

Очевидно, i_Спр=0

2.Составление характеристического уравнения и определение его корней.

Составим схему свободной составляющей. Для этого в исходной схеме после коммутации полагаем все источники равными нулю (рис.13)

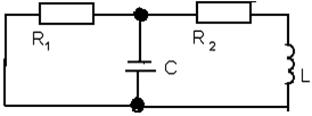
Рис. 13

Составим характеристическое уравнение методом входного сопротивления, искомый ток – ток в ветви с емкостью, поэтому делаем разрыв в этой ветви. Поскольку сопротивление емкости следует считать равным 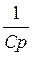, а сопротивление индуктивности – 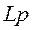, то расчетную схему представим в виде (рис.14).

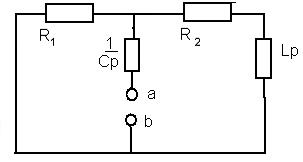
Рис. 14

Для полученной схемы запишем выражение для входного (эквивалентного) сопротивления относительно зажимов двухполюсника ab.

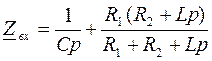
и приравняем его нулю. В результате получим характеристическое уравнение

.

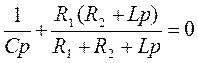После приведения к общему знаменателю будем иметь

.

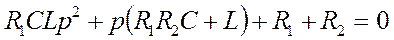Подставим значения параметров: сопротивлений в Омах, емкости в Фарадах (1мкФ=10^-6Ф) и индуктивности в Генри (1мГн=10^-3Гн). Тогда

10^-3p+0,2p+20=0.

Решим это уравнение относительно p

p₁=-100+j100, p₂=-100-j100,

т.е. корни – комплексно-сопряженные.

При комплексно-сопряженных корнях (p_1,2=α±jβ) характеристического уравнения решение искать рациональнее в виде

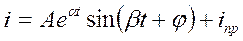, где А и φ – постоянные интегрирования.

Следовательно, получим

.

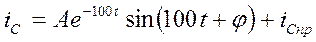3.Определение начальных условий

а) Расчет независимых начальных услови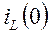й и .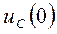

Определим значения 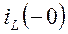и 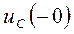,т.е. значения напряжения на емкости и тока в индуктивности в момент, непосредственно предшествующий коммутации. Для этого рассчитаем режим работы схемы до коммутации. По условию задачи в схеме с постоянными источниками до коммутации установившийся режим, т.е. установившийся режим постоянного тока. Расчетная схема установившегося режима постоянного тока до коммутации представлена на рис.15

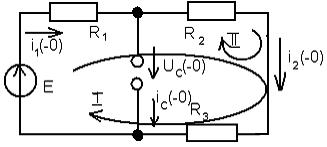
Рис. 15

Тогда по закону Кирхгофа напряжений для контуров I и II

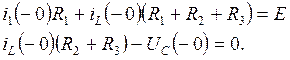
Учитывая, что 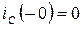(разрыв ветви), следовательно, 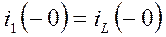, получим:

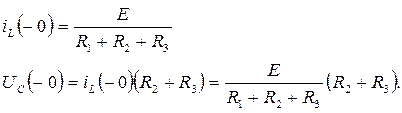
Если подставить значения параметров, то

i_L(-0)=8 A, u_C(-0)=240 В.

Искомые независимые начальные условия определяем на основании законов коммутации

.

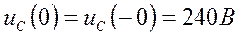
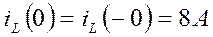б) Расчет зависимых начальных условий

Зависимость 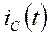содержит две постоянные интегрирования, для определения которых необходимо два начальных условия, а именно, 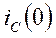и 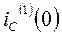. Для расчета этих величин воспользуемся резистивной схемой замещения (рис.16)

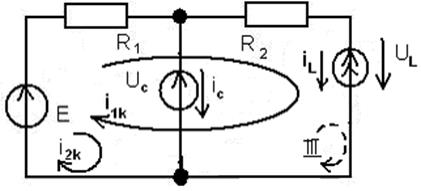
Рис. 16

По методу контурных токов

.

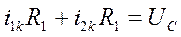Учитывая, что 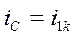, , 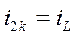получим

.

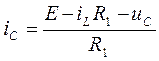Для контура III запишем уравнение по ЗКН

.

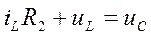Тогда

.

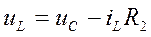В итоге необходимые уравнения для расчета зависимых начальных условий

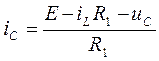(1)

.

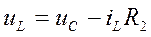Рассмотрим эти уравнения при t = 0 и рассчитаем 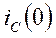и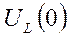

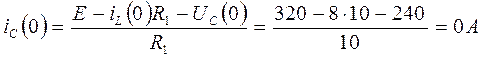
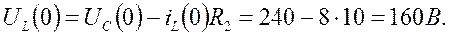
Для определения 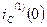продифференцируем уравнение (1) и рассмотрим его при t = 0

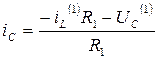для t ≥ 0

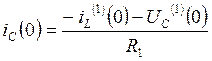для t = 0.

Рассчитаем 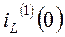и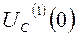

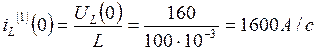
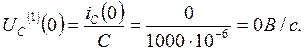
Следовательно

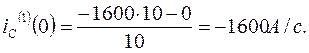
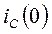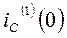Итак, зависимые начальные условия и определены.

4. Расчет постоянных интегрирования .

Выражение для тока 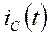с учетом найденных значений корней характеристического уравнения и принужденной составляющей имеет вид:

.

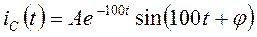Продифференцируем это выражение

.

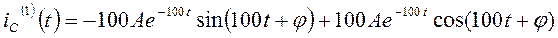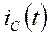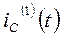Подставим в выражение для и t = 0

.

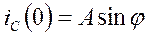
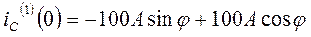С учетом зависимых начальных условий

.

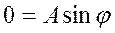
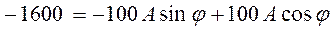Решив эту систему получим

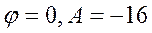или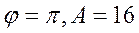

и окончательно имеем

.

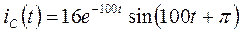Библиографический список

1. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. М.: Юрайт, 2012.

2. Зевеке Г.В. и др. Основы теории цепей. М.: Энергоатомиздат, 1989.

3. Под редакцией Бутырина П.А., Коровкина Н.В. Теоретические основы электротехники. Интернет-тестирование базовых знаний: Учебное пособие.

С-П.: ООО Изд-во «Лань», 2012.

4. Белов Н.В., Волков Ю.С. Электротехника и основы электроники: Учебное пособие. С-П.: ООО Из-во «Лань», 2012.

Учебное издание

КЛАССИЧЕСКИЙ МЕТОД РАСЧЕТА ПЕРЕХОДНЫХ ПРОЦЕССОВ В ЛИНЕЙНЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ

Составитель

ОСИПОВ Евгений Георгиевич

Редактор С.П. Клышинская

Технический редактор О.Г. Завьялова

Подписано в печать 21.01.2013. Формат 60х84/16.

Бумага офсетная. Печать – ризография.

Усл. печ. л. 1,75 Уч.-изд. л. 1,49 Тираж 50 экз.

Заказ Бесплатно Изд. № 2

Московский институт электроники и математики Национального исследовательского университета «Высшая школа экономики».

109028 Москва, Б. Трехсвятительский пер., 3.

Редакционно-издательский отдел Московского института электроники и математики Национального исследовательского университета «Высшая школа экономики».

113054 Москва, ул. М. Пионерская, 12.