Распространение модели Курно на n предприятий.

Аналитически модель Курно можно распространить на отрасль с любым количеством предприятий.

В случае монополии n=1, выпуск монополиста совпадает с общим выпуском отрасли

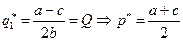
В случае дуополии n=2, 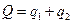мы вывели

;

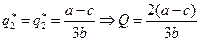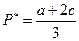
Сравнив монополию и дуополию, заметим, что отраслевой выпуск в дуополии выше, чем в случае монополии, а равновесная цена ниже, чем в монополии.

Можно показать, что с увеличением числа предприятий при сохранении уровня затрат выпуск отрасли будет увеличиваться, а цена снижаться, приближаясь к совершенно конкурентному уровню.

В случае n предприятий ( 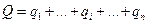), прибыль каждого из них:

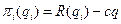
Тогда, в силу предполагаемой симметрии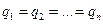

;

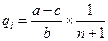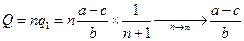
Отраслевой выпуск Q в 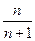раз превысит оптимальный выпуск совершенно конкурентного предприятия.

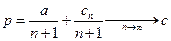
Напомним, что при совершенной конкуренции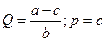

Модель Курно предсказывает снижение цены продукции и приближение её к величине предельных издержек при большом числе предприятий. «Достижения Курно не ограничиваются созданием теории чистой монополии и теории дуополии. Он … выставил идею о том, что совершенная конкуренция есть предельный случай из целого спектра рыночных структур, определенных в терминах количества продавцов» (Марк Блауг). Отсюда позже возникло представление о совершенной конкуренции как о стандарте для оценки несовершенно конкурентных рыночных структур.

Введение в теорию игр.

Принятие решения в конфликтной ситуации связано с различием интересов (целей) сторон и затрудняется из-за неопределенности в поведении противника. Для обоснования решения в условиях конфликта разработаны специальные математические методы, которые рассматриваются в теории игр. Ее возникновение относится к 1944 году, когда вышла в свет монография Неймана и Моргенштерна «Теория игр и экономическое поведение».

Под термином «игра» мы будем понимать упрощенную математическую модель рассматриваемой конфликтной ситуации. В отличие от реальности, игра ведется по определенным правилам, которые четко определяют права и обязанности участников игры, а также исход игры (выигрыш или проигрыш). Задачей теории игр является выработка рекомендаций по рациональному образу действий участников конфликта. Конфликтующие стороны назовем игроками, одну реализацию игры - партией, выбор игроком того или иного действия – ходом. Ходы бывают двух типов:

· личные (сознательные) - выбирается игроком сознательно;

· случайные – не зависят от воли игрока, определяются по результату бросания монеты или кубика и т.п.

Игры, состоящие только из личных ходов, называются стратегическими (шахматы), а игры, состоящие только из случайных ходов, называются азартными (лото). Игра конечна, если у каждого из игроков конечное число стратегий, т.е. конечное число вариантов поведения. Существует огромное количество разнообразных «игр», т.е. моделей, так как в жизни существует огромное количество конфликтных ситуаций. Можно классифицировать игры по разным признакам. Например, по продолжительности игры: на однопериодные (статические) и многопериодные (динамические), т.е. повторяемые. По количеству участников: парные игры (2 игрока) и множественные (более 2 игроков). Если игроки могут объединяться в коалиции и действовать сообща, то такие игры называют кооперативными. Мы в основном будем иметь дело с конечными стратегическими некооперативными играми.

Рассмотрим парные игры. Участников игры двое - А и В. Задано множество ходов (для статической игры ход и стратегия одно и то же) для каждого игрока. Очень важно, что результат действий одной стороны определяется неоднозначно, он зависит и от поведения второй стороны. Каждой паре ходов (чистых стратегий) ставится в соответствие пара чисел – выигрышей первого игрока и второго игрока. Таким образом, игру можно задать с помощью матрицы выигрышей, или платежной матрицы. Каждой строке этой матрицы соответствует чистая стратегия первого игрока, каждому столбцу – чистая стратегия второго игрока.

Парные игры делятся на игры с постоянной суммой выигрышей и на игры с переменной суммой выигрышей. Из игр с постоянной суммой представляют особый интерес антагонистические игры, или игры с нулевой суммой, в которых выигрыш одного игрока всегда полностью совпадает с проигрышем другого игрока. Поэтому платежная матрица антагонистической игры выглядит проще, в ней представлены выигрыши только первого игрока. Такие игры называют матричными играми.

В сложных (многоходовых) задачах понятия ход и стратегия различны, их не следует путать. Ход – вариант действия одного из игроков в какой-то момент игры. Стратегия игрока это совокупность правил, определяющих выбор варианта действий при каждом личном ходе игрока в зависимости от ситуации, сложившейся в процессе игры. Стратегию можно представить в виде полного компьютерного алгоритма для участия в игре, который предусматривает ход в любом возможном положении во время игры.