Самостоятельная работа обучающегося с преподавателем 4 страница
Определение. Огибающей однопараметрического семейства кривых на плоскости называется кривая, которая в каждой своей точке касается одной из линий семейства. Пусть однопараметрическое семейство кривых задается уравнением . (4.1) Для вычисления углового коэффициента касательной к линии семейства продифференцируем последнее уравнение по Х в предположении, что У – неявная функция от Х. Предполагаем также, что случай 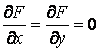 (особые точки семейства) из рассмотрения исключаются. (особые точки семейства) из рассмотрения исключаются. 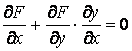 , или , или 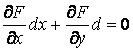 (4.2) Для записи искомого уравнения огибающей формально используем ту же функцию (4.2) Для записи искомого уравнения огибающей формально используем ту же функцию 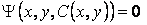 , Где, однако, , Где, однако, 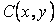 – произвольное аналитическое выражение. Отсюда получаем – произвольное аналитическое выражение. Отсюда получаем 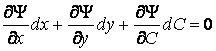 . (4.3) Поскольку угловые коэффициенты огибающей и касательной к линиям семейства в точке касания совпадают, то, сравнивая (4.1) и (4.2), получаем, что . (4.3) Поскольку угловые коэффициенты огибающей и касательной к линиям семейства в точке касания совпадают, то, сравнивая (4.1) и (4.2), получаем, что 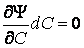 . Если . Если 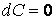 , то , то 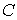  , и мы получаем заданное семейство кривых. Поэтому следует считать, что , и мы получаем заданное семейство кривых. Поэтому следует считать, что 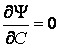 . Окончательно, для определения огибающей получаем систему уравнений . Окончательно, для определения огибающей получаем систему уравнений 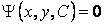 , , 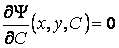 . (4.4) Исключая из системы параметр С, получим искомое уравнение огибающей. Заметим, что огибающая семейства кривых может и не существовать, а исключение параметра из системы уравнений (4.4) может привести к геометрическому месту особых точек семейства, в которых кривые не имеют касательных. Пример. Рассмотрим семейство окружностей заданного радиуса, центры которых лежат на оси ОХ: . (4.4) Исключая из системы параметр С, получим искомое уравнение огибающей. Заметим, что огибающая семейства кривых может и не существовать, а исключение параметра из системы уравнений (4.4) может привести к геометрическому месту особых точек семейства, в которых кривые не имеют касательных. Пример. Рассмотрим семейство окружностей заданного радиуса, центры которых лежат на оси ОХ: 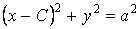 . Система уравнений (4.4) принимает вид . Система уравнений (4.4) принимает вид 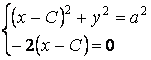 , Что приводит к двум огибающим семейства , Что приводит к двум огибающим семейства 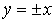 . . | |||
| 4.2. Огибающая однопараметрического семейства поверхностей |  |  |  |
Определение огибающей семейства поверхностей не отличается по сути от определения огибающей семейства кривых. Пусть имеется семейство поверхностей 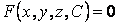 . (4.5) Фиксируя значение С, получим определенную поверхность семейства. Рассмотрим новую поверхность, которая определяется тем же уравнением, но с переменной величиной С . (4.5) Фиксируя значение С, получим определенную поверхность семейства. Рассмотрим новую поверхность, которая определяется тем же уравнением, но с переменной величиной С 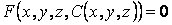 , И пусть этот переменный параметр определяется из соотношения , И пусть этот переменный параметр определяется из соотношения 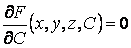 . Можно сказать, что эта поверхность определяется системой уравнений . Можно сказать, что эта поверхность определяется системой уравнений 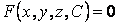 , , 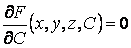 . (4.6) Покажем, что эта система определяет огибающую данного семейства поверхностей, т. е. поверхность, которая в каждой своей точке касается какой-либо поверхности семейства. Действительно, для заданного семейства (48) в силу постоянности С должно выполняться условие . (4.6) Покажем, что эта система определяет огибающую данного семейства поверхностей, т. е. поверхность, которая в каждой своей точке касается какой-либо поверхности семейства. Действительно, для заданного семейства (48) в силу постоянности С должно выполняться условие 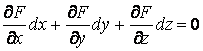 . На огибающей поверхности С – переменная величина, и мы должны записать . На огибающей поверхности С – переменная величина, и мы должны записать 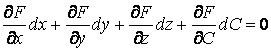 . В силу условия . В силу условия 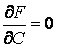 для огибающей эти два условия совпадают, т. е. бесконечно малое перемещение ( для огибающей эти два условия совпадают, т. е. бесконечно малое перемещение ( 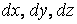 ) в общих точках огибающей и поверхности семейства ортогонально одному и тому же направлению, которое определяется вектором ) в общих точках огибающей и поверхности семейства ортогонально одному и тому же направлению, которое определяется вектором 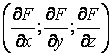 , откуда и следует доказательство искомого касания. Заметим, что огибающая семейства поверхностей может и не существовать. Пример. Рассмотрим семейство сфер заданного радиуса , откуда и следует доказательство искомого касания. Заметим, что огибающая семейства поверхностей может и не существовать. Пример. Рассмотрим семейство сфер заданного радиуса 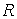 , центры которых находятся на оси , центры которых находятся на оси  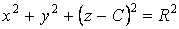 . Дифференцируя по С, имеем . Дифференцируя по С, имеем 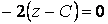 . Исключая из этих уравнений С, получим уравнение кругового цилиндра . Исключая из этих уравнений С, получим уравнение кругового цилиндра 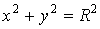 , Который касается каждой из сфер данного семейства. , Который касается каждой из сфер данного семейства. | |||
| 5. Некоторые приложения дифференциальной геометрии к механике |  |  |  |
| Векторные функции находят широкое применение в физике, механике, электротехнике и других естественных и технических науках (при изучении параметров движения различных материальных систем, при определении деформаций и напряжений в элементах конструкций, при исследовании колебаний в механических, электрических и других системах). Соответствующие задачи, как правило, содержат элементы исследований, составляющие предмет дифференциальной геометрии, в частности, исследования криволинейных траекторий движения, форм, которые приобретают под действием нагрузки деформированные элементы машин и сооружений и др. Рассмотрим некоторые из этих задач. | |||
| 5.1. Способы описания движения точки. Координатный способ задания движения точки |  |  |  |
Механика изучает движение. Кинематика – это раздел теоретической механики, в котором для различных законов движения в пространстве геометрических объектов, таких как точка или тело, определяют их кинематические характеристики. К основным кинематическим характеристикам движения относят: Траектории, Скорости и Ускорения. Основная задача кинематики состоит в определении кинематических характеристик движения по заданному для него закону. Решение основной задачи кинематики для движущихся геометрических объектов (точки, тела) рассматривают в определенной системе отсчета. Любые три независимые величины 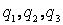 , однозначно определяющие положение точки в трехмерном пространстве, могут рассматриваться как координаты этой точки. При этом радиус-вектор точки является функцией этих координат, т. е. , однозначно определяющие положение точки в трехмерном пространстве, могут рассматриваться как координаты этой точки. При этом радиус-вектор точки является функцией этих координат, т. е. 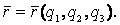 При изменении одной из координат и фиксированных остальных конец радиус-вектора При изменении одной из координат и фиксированных остальных конец радиус-вектора 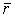 вычерчивает линию, которую называют координатной линией Координатные линии, вообще говоря, кривые, и поэтому координаты называют криволинейными. Единичные орты вычерчивает линию, которую называют координатной линией Координатные линии, вообще говоря, кривые, и поэтому координаты называют криволинейными. Единичные орты 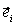 , направленные по касательным к координатным линиям в точке М пространства в сторону возрастания соответствующих координат, определяют в каждой точке пространства криволинейную систему координат, причем , направленные по касательным к координатным линиям в точке М пространства в сторону возрастания соответствующих координат, определяют в каждой точке пространства криволинейную систему координат, причем 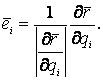 Вектор скорости Вектор скорости 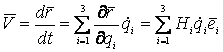 , (5.1) Где , (5.1) Где 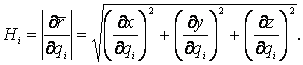 (5.2) Равенство (5.1) представляет собой разложение (но не ортогональное проектирование!) вектора скорости по осям криволинейной системы координат. Ортогональные проекции (5.2) Равенство (5.1) представляет собой разложение (но не ортогональное проектирование!) вектора скорости по осям криволинейной системы координат. Ортогональные проекции  вектора скорости на оси вектора скорости на оси  Равны Равны 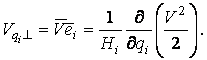 (5.3) Коэффициенты Hi называются коэффициентами Ламе и находятся из соотношения (5.3) Коэффициенты Hi называются коэффициентами Ламе и находятся из соотношения 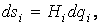 Где DSi – дифференциал дуги I-ой координатной линии при изменении I-ой координаты и фиксированных остальных. В самом деле, в прямоугольной системе координат DS2 = dx2+ dy2+ dz2, (5.5) Но Где DSi – дифференциал дуги I-ой координатной линии при изменении I-ой координаты и фиксированных остальных. В самом деле, в прямоугольной системе координат DS2 = dx2+ dy2+ dz2, (5.5) Но 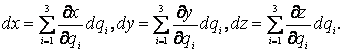 Подставляя значения Dx, dy, dz в (5.5), получим Подставляя значения Dx, dy, dz в (5.5), получим 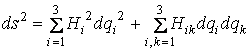 , (5.6) Где , (5.6) Где 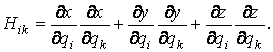 Предполагая, что изменяется лишь одна координата, а две другие фиксированы, получим (5.4), т. е. коэффициенты Ламе получаются как множители дифференциалов координат в выражениях для дифференциалов дуг соответствующих координатных линий. Если система криволинейных координат ортогональна, т. е. если при Предполагая, что изменяется лишь одна координата, а две другие фиксированы, получим (5.4), т. е. коэффициенты Ламе получаются как множители дифференциалов координат в выражениях для дифференциалов дуг соответствующих координатных линий. Если система криволинейных координат ортогональна, т. е. если при 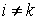 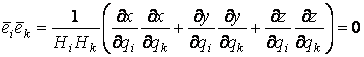 , (5.7) То Hik = 0 и , (5.7) То Hik = 0 и 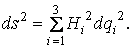 Поэтому в случае ортогональной системы координат для модуля вектора скорости получаем Поэтому в случае ортогональной системы координат для модуля вектора скорости получаем 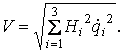 (5.8) Ортогональные проекции вектора ускорения (5.8) Ортогональные проекции вектора ускорения 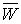 точки на оси произвольной криволинейной системы координат имеют вид точки на оси произвольной криволинейной системы координат имеют вид 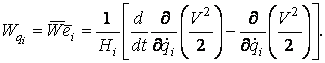 (5.9) Как видно из формулы (5.9), проекции ускорения на координатные оси qi получаются дифференцированием выражения для квадрата скорости. При этом следует иметь в виду, что (5.9) Как видно из формулы (5.9), проекции ускорения на координатные оси qi получаются дифференцированием выражения для квадрата скорости. При этом следует иметь в виду, что 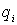 и и 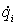 независимы, что отражает факт независимости следующих событий: находиться в какой-либо точке пространства и иметь в этой точке какую-либо скорость. Кроме того, изучается не движение по некоторой заданной траектории, а способ описания любых движений. Иначе говоря, рассматривается вся совокупность допустимых движений, и выбор точки пространства задает только ее положение, никак не ограничивая направление и величину вектора скорости. независимы, что отражает факт независимости следующих событий: находиться в какой-либо точке пространства и иметь в этой точке какую-либо скорость. Кроме того, изучается не движение по некоторой заданной траектории, а способ описания любых движений. Иначе говоря, рассматривается вся совокупность допустимых движений, и выбор точки пространства задает только ее положение, никак не ограничивая направление и величину вектора скорости. 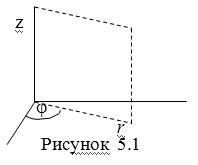 Пример 1. Для движущейся точки найти скорость и проекции ускорения на касательные к координатным линиям цилиндрической системы координат Пример 1. Для движущейся точки найти скорость и проекции ускорения на касательные к координатным линиям цилиндрической системы координат 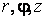 (рис. 5.1). Решение. Так как система координат ортогональна, то (рис. 5.1). Решение. Так как система координат ортогональна, то 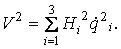 Найдем коэффициенты Ламе, рассматривая элементы дуг вдоль соответствующих координатных линий: Найдем коэффициенты Ламе, рассматривая элементы дуг вдоль соответствующих координатных линий: 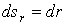 , откуда имеем , откуда имеем 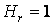 , , 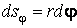 , откуда имеем , откуда имеем 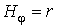 , , 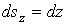 , откуда имеем , откуда имеем 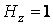 . Следовательно, . Следовательно, 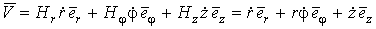 , , 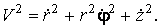 Выполняя операции дифференцирования в соответствии с формулой (5.9), получаем Выполняя операции дифференцирования в соответствии с формулой (5.9), получаем 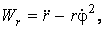 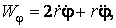 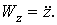 При движении точки в плоскости Z = const первые две компоненты ускорения задают радиальную При движении точки в плоскости Z = const первые две компоненты ускорения задают радиальную 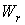 и трансверсальную и трансверсальную 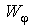 Компоненты ускорения в полярной системе координат. Компоненты ускорения в полярной системе координат. | |||
| 5.2. Описание движения точки с помощью осей естественного трехгранника |  |  |  |
Подвижный базис, который сопровождает точку М при её движении по кривой, во втором разделе назван Естественным базисом или Трехгранником Френе (рис. 2.1). Кривую, которая образуется при движении материальной точки, называют траекторией. В каждой точке траектории можно построить три взаимно перпендикулярные оси, непосредственно связанные с траекторией. Если начало их помещено в движущуюся точку, то оси, направленные по касательной, нормали и бинормали траектории ( 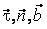 – единичные орты этой системы) называются естественными осями. Вектор скорости – единичные орты этой системы) называются естественными осями. Вектор скорости 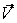 направлен по касательной к траектории направлен по касательной к траектории 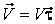 . Вектор ускорения . Вектор ускорения 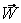 всегда лежит в соприкасающейся плоскости траектории, и поэтому проекция его на бинормаль равна нулю всегда лежит в соприкасающейся плоскости траектории, и поэтому проекция его на бинормаль равна нулю 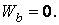 Проекции вектора ускорения Проекции вектора ускорения 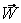 на касательную и главную нормаль к траектории равны соответственно на касательную и главную нормаль к траектории равны соответственно 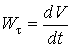 , ,  , (5.10) Где , (5.10) Где 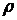 – радиус кривизны траектории в данной точке. Пример 2. Найти касательное – радиус кривизны траектории в данной точке. Пример 2. Найти касательное 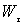 и нормальное и нормальное 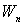 ускорения точки, а также радиус кривизны ускорения точки, а также радиус кривизны 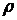 ее траектории, если движение точки выражается уравнениями ее траектории, если движение точки выражается уравнениями 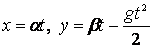 , , 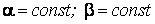 . Решение. Для определения касательного и нормального ускорения найдем сначала скорость . Решение. Для определения касательного и нормального ускорения найдем сначала скорость 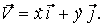 Так как Так как 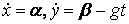 , то , то 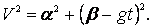 Откуда Откуда 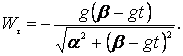 Так как радиус кривизны траектории неизвестен, найдем нормальное ускорение Так как радиус кривизны траектории неизвестен, найдем нормальное ускорение  из равенства из равенства 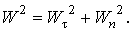 Для этого нужно сначала найти Для этого нужно сначала найти 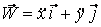 . Так как . Так как 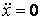 , , 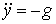 , то , то 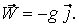 Поэтому Поэтому  Теперь нетрудно определить Теперь нетрудно определить 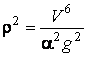 , , 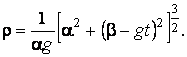 Пример 3. Движение электрона в магнитном поле описывается уравнениями Пример 3. Движение электрона в магнитном поле описывается уравнениями 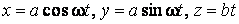 , (5.11) Где А>0, B>0, , (5.11) Где А>0, B>0, 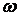 – постоянные величины. Найти уравнение траектории, скорость и ускорение электрона в цилиндрических координатах. Решение. Зависимость между декартовыми и цилиндрическими координатами выражается соотношениями – постоянные величины. Найти уравнение траектории, скорость и ускорение электрона в цилиндрических координатах. Решение. Зависимость между декартовыми и цилиндрическими координатами выражается соотношениями 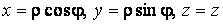 , что позволяет записать уравнения движения электрона в цилиндрических координатах в виде: , что позволяет записать уравнения движения электрона в цилиндрических координатах в виде: 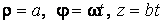 . (5.12) Из уравнений (5.12) следует, что электрон движется по винтовой линии на цилиндре радиуса А. Если предположить, что B>0, . (5.12) Из уравнений (5.12) следует, что электрон движется по винтовой линии на цилиндре радиуса А. Если предположить, что B>0, 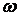 > 0, то траектория электрона – правая винтовая линия в полупространстве > 0, то траектория электрона – правая винтовая линия в полупространстве 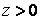 (рис. 5.2). (рис. 5.2). 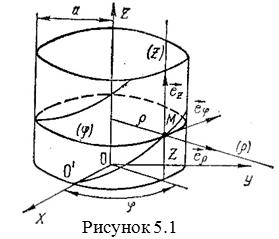 Уравнение траектории находим, исключая Уравнение траектории находим, исключая 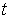 из (5.12): из (5.12): 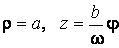 . Отсюда видно, что винтовая линия получается “наклеиванием” прямой . Отсюда видно, что винтовая линия получается “наклеиванием” прямой 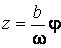 на цилиндр радиуса А. Скорость электрона определим по формуле (5.1). В рассматриваемом случае она принимает вид на цилиндр радиуса А. Скорость электрона определим по формуле (5.1). В рассматриваемом случае она принимает вид 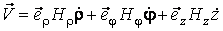 . (5.13) Из уравнений (5.12) следует, что . (5.13) Из уравнений (5.12) следует, что 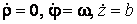 . Параметры Ляме определяем на основании формул (5.2): . Параметры Ляме определяем на основании формул (5.2): 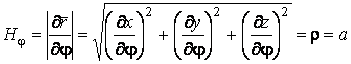 , (5.14) , (5.14) 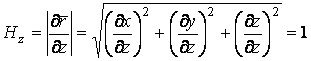 . (5.15) Равенство (5.13) на основании соотношений (5.14) – (5.15) принимает вид . (5.15) Равенство (5.13) на основании соотношений (5.14) – (5.15) принимает вид 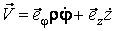 , , 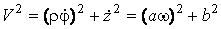 . Отсюда следует, что электрон движется по винтовой линии с постоянной скоростью. Проекции ускорения электрона определяем по формулам (5.9), которые в рассматриваемом случае имеют следующий вид: . Отсюда следует, что электрон движется по винтовой линии с постоянной скоростью. Проекции ускорения электрона определяем по формулам (5.9), которые в рассматриваемом случае имеют следующий вид: 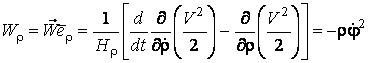 , (5.16) , (5.16) 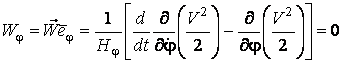 , (5.17) , (5.17) 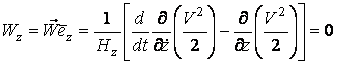 . (5.18) Вычисляя, находим . (5.18) Вычисляя, находим 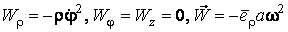 . (5.19) Из формул (5.19) следует, что вектор ускорения электрона имеет постоянную величину и направлен вдоль радиуса цилиндра к его оси. Пример 4. Движение точки М Задано в тороидальной системе координат . (5.19) Из формул (5.19) следует, что вектор ускорения электрона имеет постоянную величину и направлен вдоль радиуса цилиндра к его оси. Пример 4. Движение точки М Задано в тороидальной системе координат 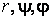 (рис. 5.3). Определить вектор скорости и вектор ускорения точки в этих координатах. Решение. На основании рисунка находим зависимость между декартовыми и тороидальными координатами: (рис. 5.3). Определить вектор скорости и вектор ускорения точки в этих координатах. Решение. На основании рисунка находим зависимость между декартовыми и тороидальными координатами: 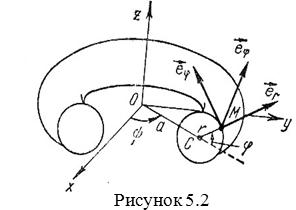 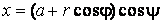 , , 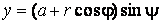 , , 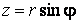 . По формулам (5.2) определяем параметры Ляме: . По формулам (5.2) определяем параметры Ляме: 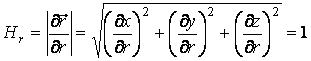 , , 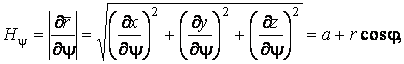 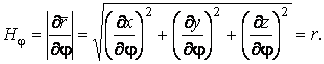 Векторы скорости и ускорения определяем из соотношений (5.1) –(5.3) и (5.9): Векторы скорости и ускорения определяем из соотношений (5.1) –(5.3) и (5.9): 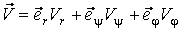 , , 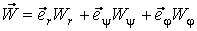 , , 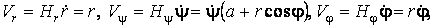 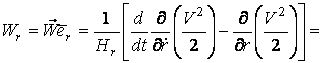 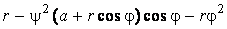 , , 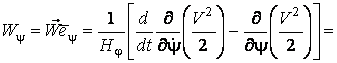 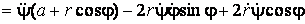 , , 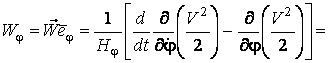 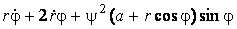 , Где , Где 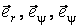 – орты тороидальных осей координат (рис. 5.3). – орты тороидальных осей координат (рис. 5.3). |
