Вычисление пределов функции с помощью замены бесконечно малых на эквивалентные.
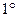 Функция называется
Функция называется 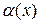 бесконечно малой при
бесконечно малой при 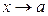 (или в точке
(или в точке 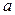 ), если
), если 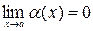 .
.
Пусть 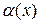 и
и 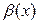 - две бесконечно малые функции при
- две бесконечно малые функции при 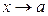 .
.
1) Если 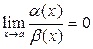 , то
, то 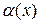 называются бесконечно малой более высокого порядка чем
называются бесконечно малой более высокого порядка чем 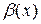 (при
(при 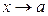 );
);
2) Если 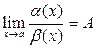 , то
, то 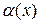 и
и 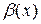 называются бесконечно малыми одного порядка (при
называются бесконечно малыми одного порядка (при 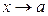 );
);
3) Если 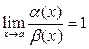 , то
, то 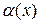 и
и 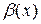 называются эквивалентными бесконечно малыми (при
называются эквивалентными бесконечно малыми (при 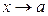 ). Эквивалентность обозначается так:
). Эквивалентность обозначается так: 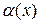 ~
~ 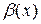 при
при 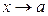 .
.
 Приведем таблицу эквивалентных бесконечно малых функций при
Приведем таблицу эквивалентных бесконечно малых функций при 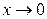 :
:
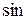
 ~
~  ,
, 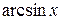 ~
~  ,
, 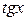 ~
~  ,
, 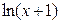 ~
~  ,
, 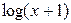 ~
~ 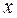
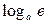 ,
,
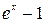 ~
~  ,
, 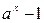 ~
~ 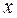
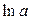 ,
, 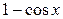 ~
~ 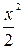 ,
, 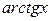 ~
~  ,
, 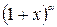 ~
~ 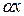 ,
,
Пример 5. Найти пределы:
а) 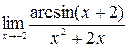 , б)
, б) 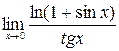 .
.
Решение. а) 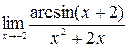 =
= 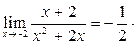
б) 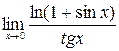 =
= 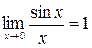 .
.
Пример 6. Найти предел:
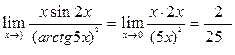 .
.
Контрольные вопросы:
1. Понятие последовательности.
2. Понятие предела последовательности
4. Определение предела функции.
5. Свойства пределов.
6. Два замечательных предела.
7. Понятие эквивалентных бесконечно малых функций.
8.Вычисление пределов функции с помощью замены бесконечно малых на эквивалентные.
Задания.
1. Вычислить пределы:
а) 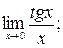 б)
б) 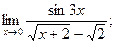 в)
в) 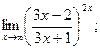 г)
г) 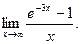
2.Найти пределы последовательностей:
1) 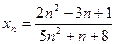 ; 2)
; 2) 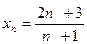 ; 3)
; 3) 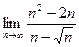 ;
;
4) 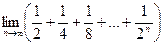 ; 5)
; 5) 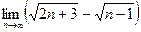
3. Пользуясь методом замены бесконечно малых эквивалентными вычислить следующие пределы:
а) 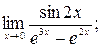 б)
б) 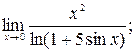 в)
в) 
Занятие 3.
Непрерывность функции
 Функция
Функция 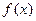 называется непрерывной в точке
называется непрерывной в точке 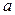 , если:
, если:
1) эта функция определена в некоторой окрестности точки 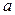 ;
;
2) существует 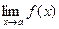 ;
;
3) этот предел равен значению функции в точке 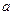 , т.е.
, т.е. 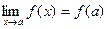 ,
,
Обозначая 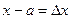 (приращение аргумента) и
(приращение аргумента) и 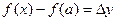 , (приращение функции), условие непрерывности можно записать так:
, (приращение функции), условие непрерывности можно записать так: 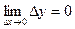 , т.е. функция
, т.е. функция 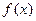 непрерывна в точке
непрерывна в точке 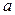 тогда и только тогда, тогда в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
тогда и только тогда, тогда в этой точке бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Если функция непрерывна в каждой точке некоторой области (интервала, сегмента и т.п.), то она называется непрерывной в этой области.
 Функция
Функция 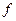 называется непрерывной в точке
называется непрерывной в точке 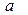 справа, если выполняется условие
справа, если выполняется условие 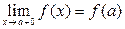 (когда
(когда 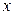 стремится к
стремится к 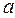 справа, оставаясь больше
справа, оставаясь больше 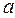 ).
).
Если 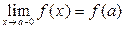 , то говорят, что функция
, то говорят, что функция 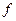 непрерывна слева (когда
непрерывна слева (когда 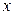 стремится к
стремится к 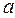 слева, оставаясь меньше
слева, оставаясь меньше 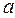 ).
).
.
Если 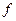 непрерывна в точке
непрерывна в точке 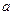 слева и справа, то она непрерывна в этой точке.
слева и справа, то она непрерывна в этой точке.
 Функция
Функция 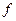 имеет разрыв в точке
имеет разрыв в точке 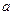 , если она определена в сколь угодно близких точках к
, если она определена в сколь угодно близких точках к 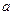 , но в самой точке
, но в самой точке 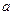 нарушается хотя бы одно из условий непрерывности функции.
нарушается хотя бы одно из условий непрерывности функции.
Конечным разрывом или разрывом первого рода называется разрыв функции 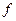 в точке
в точке 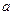 , если существуют конечные односторонние пределы
, если существуют конечные односторонние пределы
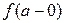 и
и 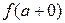 .
.
Скачком функции 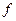 в точке
в точке 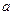 называется разность его односторонних пределов
называется разность его односторонних пределов 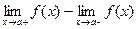 , если они различны.
, если они различны.
Если 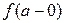 =
= 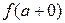 , то точка
, то точка 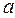 называется точкой устранимого разрыва.
называется точкой устранимого разрыва.
Все другие случаи разрыва функции называются разрывами 2-го рода.
Если хотя бы один из указанных односторонних пределов окажется бесконечным, то разрыв функции называется бесконечным.
Пример 1.
Исследовать функцию на непрерывность; непрерывность справа и слева и установить характер точек разрыва, где

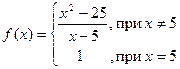
Решение. При 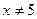 можно сократить на
можно сократить на 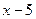 .
.
Следовательно, 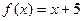 при
при 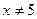 . Легко
. Легко
видеть, что 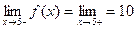 . Значит, при
. Значит, при 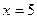 функция будет разрывной, так как предел функции не равен значению функции в этой точке.
функция будет разрывной, так как предел функции не равен значению функции в этой точке.
Пример 2. Исследовать на непрерывность функцию
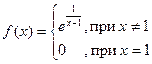
Решение.Найдем односторонние пределы в точке 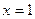 , т.е.
, т.е.
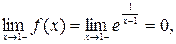
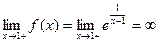 .
.
В точке 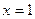 функция
функция 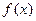 имеет разрыв 2 рода. Так как предел слева в точке
имеет разрыв 2 рода. Так как предел слева в точке 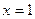 равен значению функции в этой точке, то функция непрерывна слева в точке
равен значению функции в этой точке, то функция непрерывна слева в точке 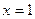 . При остальных значениях
. При остальных значениях 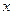 функция непрерывна (по теореме непрерывности суперпозиции функций).
функция непрерывна (по теореме непрерывности суперпозиции функций).
Пример 3.Доказать непрерывность функции 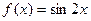 .
.
Решение.Пусть 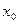 - произвольное значение на числовой прямой.
- произвольное значение на числовой прямой.
Найдем 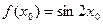 и составим разность
и составим разность
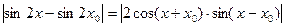
Оценим полученное выражение в правой части по абсолютной величине
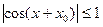 ,
,
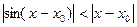 .
.
Итак, отмечаем, что
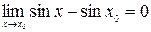 .
.
Контрольные вопросы
1. Определение непрерывной функции в точке.
2. Разрыв функции в точке. Классификация разрывов.
3. Свойства непрерывных функций.
Задания.
1) Показать, что при 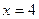 функция
функция 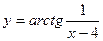 имеет разрыв.
имеет разрыв.
2) Найти точки разрыва функции 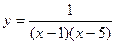 .
.
3) Каков характер разрыва функции 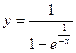 в точке
в точке 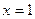 .
.
4) Исследовать на непрерывность функции
а) 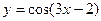 ; б)
; б) 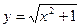
Занятие 4
Производная функции
 Пусть функция
Пусть функция 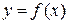 определена на интервале
определена на интервале 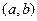 .Определим:
.Определим:
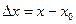 - приращение аргумента
- приращение аргумента 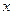 в точке
в точке 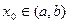 , а
, а
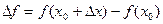 - приращение функции в точке
- приращение функции в точке 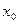 .
.
Если существует конечный предел
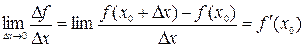 ,
,
то он называется производной функции 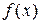 в точке
в точке 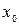 .
.
Значение производной 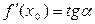 -есть угловой коэффициент касательной к графику функции
-есть угловой коэффициент касательной к графику функции 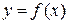 в точке, абсцисса которой есть
в точке, абсцисса которой есть 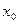
Если 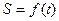 - закон прямолинейного движения точки, то первая производная пути по времени
- закон прямолинейного движения точки, то первая производная пути по времени 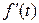 -есть скорость этого движения.
-есть скорость этого движения.
