Описание метода определения параметров аппроксимирующей функции (решение системы нормальных уравнений)

А. Метод Гаусса:

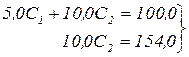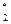С =15,4 ; С 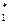= -10,8

Б. Метод обратной матрицы:

для матрицы A =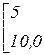

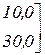
обратная матрица имеет вид

A^{-1 = ,}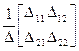

где 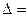det A - определитель матрицы А;

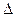_{i j} - алгебраическое дополнение.

Отсюда det A = 5 · 30,0 – 10,0 · 10,0 = 50,0.

A^-1 =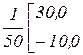

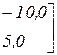
8. Контрольный расчет параметров аппроксимирующей функции(без использования компьютера).

Решение системы уравнений A C = B методом обратной матрицы имеет вид C^* = A^-1 B, т.е.

C^* = .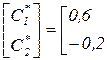

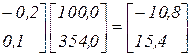Запись искомой аппроксимирующей функции y(x)

y = –10,8 + 15,4 x .

Оценка погрешности аппроксимации.

Для оценки среднеквадратичного и максимального по модулю отклонений аппроксимирующей функции от исходной представим результаты проведенных вычислений в виде табл. 2 и рис. 1.

Таблица 2

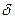i	xi	yi	y(xi)	i = yi – y(xi)
	0,0 1,0 2,0 3,0 4,0	0,0 1,0 8,0 27,0 64,0	–10,8 4,6 20,0 35,4 50,8	10,8 –3,6 –12,0 –8,4 13,2

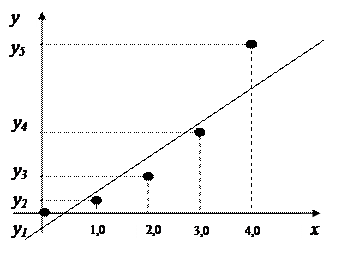Рис. 1. График функций y=f(x), y=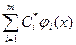

Тогда минимальное значение качества аппроксимации

J_min = J(C 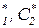) = (10,8)² + (–3,6)² + (–12,0)² + (–8,4)² + (13,2)² = 518,4,

а максимальное по модулю отклонение, получаемое сопоставлением найденных значений 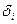, составляет

max| 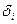| = 13,2 при x = x₅ = 4,0 .