Определение предела функции
Контрольные задания и методические рекомендации для студентов заочного обучения
Севастополь 2013 г.
УДК
Авт №
ББК
Березнева С.М., Тарлецкая Л.П., Маркина Е.В.
Настоящее учебное пособие предназначено для самостоятельной работы студентов заочной формы обучения, изучающих курс высшей математики на факультетах «Судовождение и энергетика судов» и «Радиотехника и защита информации» на первом и втором курсах. Оно охватывает все разделы дисциплины «высшая математика», предусмотренные программой.
Контрольные задания основаны на методических разработках преподавателей высшей математики кафедрыОН и ИД академии ВМСУ им П.С. Нахимова.
Рецензент: О.Г. Сатыга, к.т.н., доцент
©Академиявоенно-морских сил имени П.С. Нахимова, 2013
ПРЕДИСЛОВИЕ.
Пособие содержит материалы, необходимые для подготовки к успешной сдаче экзаменов по дисциплине «высшая математика» в І, ІІ, ІІІ, IV учебных семестрах.
В каждом семестре предусмотрено выполнение учащимися заданий модульного контроля по указаным темам. Материалы пособия, относящиеся к определённому семестру, содержат:
· краткое изложение основных теоретических сведений;
· примеры выполнения типовых практических задач;
· контрольные вопросы по теоретическому материалу, вынесенные на семестровый экзамен;
· типовые практические задачи для самостоятельного выполнения (десять вариантов) по каждому модулю;
В сборнике приведён список рекомендуемой литературы по каждому модулю.
I семестр
Вопросы
1. Классификация систем линейных алгебраических уравнений и их решений.
2. Матрицы систем линейных алгебраических уравнений и их виды.
3. Определитель квадратной матрицы и его вычисление.
4. Обратная матрица и ее нахождение.
5. Решение и исследование систем линейных алгебраических уравнений по формулам Крамера.
6. Решение и исследование систем линейных алгебраических уравнений матричным способом.
7. Решение и исследование систем линейных алгебраических уравнений по способу Гаусса.
8. Скалярные и векторные величины, линейные операции над векторами.
9. Скалярное произведение векторов и его свойства. Угол между двумя векторами. Условие перпендикулярности двух векторов.
10. Векторное произведение векторов и его свойства. Условие коллинеарности двух векторов.
11. Смешанное произведение векторов и его свойства. Условие компланарности трех векторов.
12. Прямая линия на плоскости. Виды уравнения прямой.
13. Основные задачи на прямую линию на плоскости.
14. Канонические уравнения линий второго порядка. Их характерные точки и линии.
15. Плоскость. Различные виды уравнений плоскости. Уравнение плоскости, проходящей через три точки.
16. Основные задачи на плоскость.
17. Уравнение прямой в пространстве.
18. Основные задачи на прямую в пространстве.
19. Пределы функций и числовых последовательностей.
20. Теоремы о пределах суммы, произведения и частного функций.
21. Неопределенные выражения и их раскрытие.
22. Первый и второй замечательные пределы.
23. Непрерывность функций. Точки разрыва.
24. Производная и дифференциал функций.
25. Дифференцирование суммы, произведения и частного функций.
26. Дифференцирование сложной функции.
27. Дифференцирование функции, заданной неявно и параметрически.
28. Уравнения касательной прямой и нормали к графику функции.
29. Повторное дифференцирование.
30. Исследование функций и построение графиков.
31. Комплексные числа и действия над ними.
Модуль 1
Линейная алгебра. Векторная алгебра
Задачи для решения.
Задание 1
Исследовать систему по теореме Кронекера-Капелли, если система совместна и определена, то решить по формулам Крамера, матричным способом и способом Гаусса.
Варианты
1. 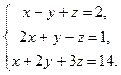 2.
2. 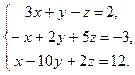
3. 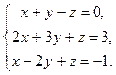 4.
4. 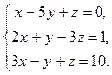
5. 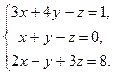 6.
6. 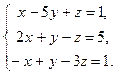
7. 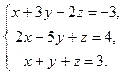 8.
8. 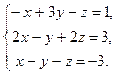
9. 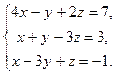 10.
10. 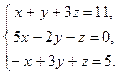
Задание 2
Даны координаты вершин пирамиды А1 А2 А3 А4:
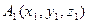 ,
, 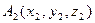 ,
, 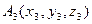 ,
, 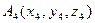 .
.
Найти:
а) длину ребра [А1А 2];
б) угол между ребрами [А1А2] и [А1 А4];
в) проекцию вектора 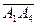 на
на 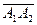 ;
;
г) площадь грани А1 А2 А3 ;
д) объем пирамиды А1 А2 А3 А4.
Варианты .
1. А1(3,1,4), А2 (-1,6,1), А3 (-1,1,6), А4(0,4,-1);
2. А1 (3,3,9), А2 (6,9,1), А3(1,7,3), А4(8,5,8);
3. А1(3,5,4), А2 (5,8,3), А3 (1,9,9), А4(6,4,8);
4. А1 (2,4,3), А2 (7,6,3), А3 (4,9,3), А4(3,6,7);
5. А1 (9,5,5), А2 (-3,7,1), А3(5,7,8), А4(6,9,12);
6. А1 (0,7,1), А2 (4,1,5), А3 (4,6,3), А4(3,9,8);
7. А1 (5,5,4), А2 (3,8,4), А3(3,5,10), А4(5,8,2);
8. А1(6,1,1), А2(4,6,6), А3(4,2,0), А4(1,2,6);
9. А1(7,5,3), А2 (9,4,4), А3 (4,5,7), А4(7,9,6);
10. А1(6,6,2), А2(5,4,7), А3(2,4,7), А4(7,3,0).
Решение типовых задач
Задание 1
Исследовать систему по теореме Кронекера-Капелли, если система совместна и определена, то решить по формулам Крамера, матричным способом и способом Гаусса.
Если система совместна, но не определена, найти общее и одно частное решение.
а) 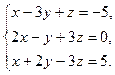 б)
б) 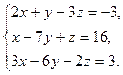
в) 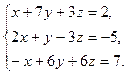
Задание 2
Даны координаты вершин пирамиды А1 А2 А3 А4.
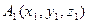 ,
, 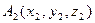 ,
, 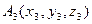 ,
, 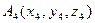 .
.
Найти:
а) длину ребра [А1А2];
б) угол между ребрами [А1А2] и [А1 А4];
в) проекцию вектора 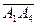 на
на 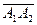 ;
;
г) площадь грани А1 А2 А3 ;
д) объем пирамиды А1 А2 А3 А4.
А1 (3;2-3), А2 (5;1;-1), А3 (-1;2; -1), А4 (1;-2;1).
Пример выполнения задания 1
а) Дана система линейных алгебраических уравнений:
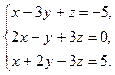
Найдём ранг матрицы А, составленной из коэффициентов при неизвестных. Путём элементарных преобразований приведём эту матрицу к ступенчатому виду.
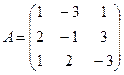 ~
~ 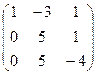 ~
~ 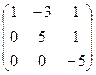 .
.
Ранг матрицы системы r(A)=3 .
Найдём ранг расширенной матрицы 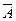 .
.
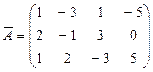 ~
~ 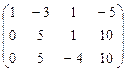 ~
~ 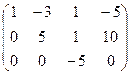 .
.
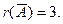
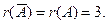
Ранг расширенной матрицы равен рангу матрицы А и числу неизвестных, следовательно, система совместна и обладает единственным решением. Найдём это решение по формулам Крамера, которые имеют вид:
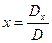 ,
, 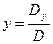 ,
, 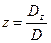 .
.
Находим основной определитель системы:
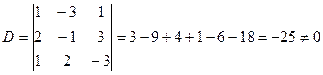 .
.
Определитель системы не равен нулю, это так же означает, что система имеет единственное решение.
Находим определители неизвестных.
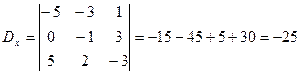 ,
,
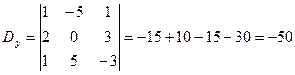 ,
,
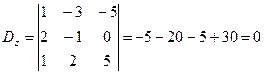 .
.
Подставив найденные значения определителей в формулы
Крамера, получим решение системы.
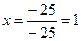 ,
, 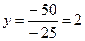 ,
, 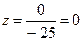 .
.
Ответ: х =1, у =2, z =0.
Решим данную систему матричным способом.
Эта система уравнений может быть записана в виде следующего матричного уравнения: AХ=B.
Матричное решение имеет вид: Х =А-1В.
Найдём матрицу А-1 обратную матрице системы: 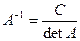 .
.
Матрица системы имеет вид:
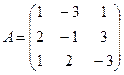 .
.
Её определитель det A уже найден: det A = D = - 25.
Составим транспонированную матрицу:
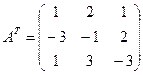 .
.
Составляем присоединенную (союзную) матрицу С, состоящую из алгебраических дополнений элементов матрицы АТ, для чего вычисляем алгебраические дополнения элементов транспонированной матрицы:
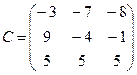 .
.
Находим решение системы в матричной форме:
Х = 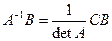 =
= 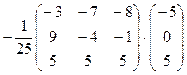 ,
,
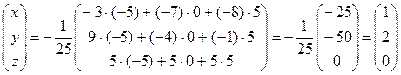 .
.
Ответ: х = 1, у = 2, z = 0.
Решим данную систему методом Гаусса.
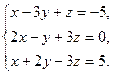
Исключим х из второго и третьего уравнения. Для этого из второго уравнения вычтем удвоенное первое, из третьего уравнения вычтем первое.
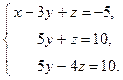
Исключим из третьего уравнения у. Для этого вычтем из него второе уравнение.
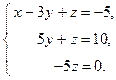
Из третьего уравнения находим z. Подставив его значение во второе уравнение, найдём у. Подставив значения х и у в первое уравнение, найдём х.
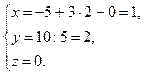
Ответ: х = 1, у = 2, z = 0.
б) Дана система линейных алгебраических уравнений:
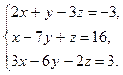
Найдём ранг матрицы А, составленной из коэффициентов при неизвестных.
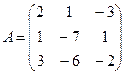 ~
~ 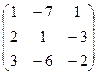 ~
~ 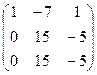 ~
~ 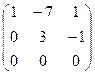
Её ранг r (A) = 2.
Найдём ранг расширенной матрицы 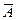 .
.
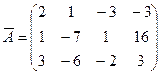 ~
~ 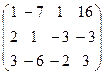 ~
~ 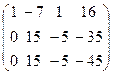 ~
~ 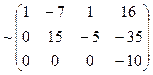 .
.
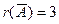 .
.
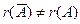 .
.
Ответ: Система не совместна.
в) Дана система линейных алгебраических уравнений:
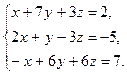
Найдём ранг матрицы А, составленной из коэффициентов при неизвестных.
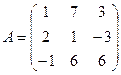 ~
~ 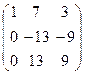 ~
~ 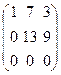 .
.
Её ранг r (A) = 2.
Найдём ранг расширенной матрицы системы.
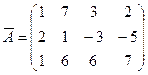 ~
~ 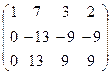 ~
~ 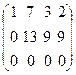 .
.
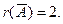
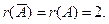
Система совместна, но не определена. Найдём решение этой системы. Восстановим систему по последней матрице.
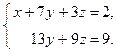
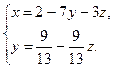
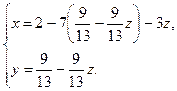 .
.
Ответ: 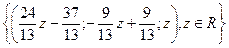 .
.
Пример выполнения задания 2
Даны координаты вершин пирамиды А1А2А3А4:
А1 (3;2;-3), А2 (5;1;-1), А3 (-1;2; -1), А4 (1;-2;1).
Найдём координаты 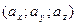 ,
, 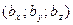 ,
, 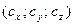
векторов 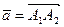 ;
; 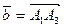 ;
; 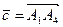 .
.
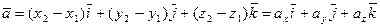 .
.
Получим:
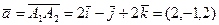 ,
,
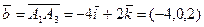 ,
,
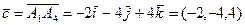 .
.
а) Длина ребра [А1 А2] пирамиды равна длине вектора 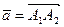 . Длина вектора определяется по формуле:
. Длина вектора определяется по формуле:
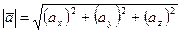 , следовательно:
, следовательно:
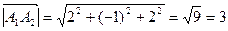 .
.
б) Угол 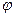 между рёбрами [А1А2] и [А1 А3] пирамиды равен углу между векторами
между рёбрами [А1А2] и [А1 А3] пирамиды равен углу между векторами 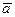 и
и 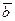 . Косинус угла между векторами определяется по формуле:
. Косинус угла между векторами определяется по формуле:
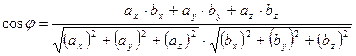 ,
,
следовательно,
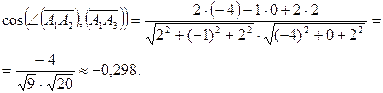
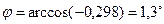 .
.
в) Проекция вектора 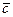 на направление вектора
на направление вектора 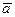 определяется
определяется
по формуле: 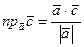 , следовательно,
, следовательно,
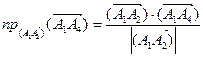 ,
,
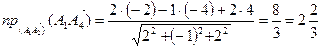 .
.
г) Определим площадь грани (А1А2А3) по формуле для вычисления площади треугольника с помощью модуля векторного произведения векторов 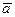 и
и 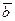 :
:
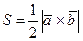 , где
, где 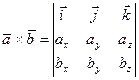 .
.
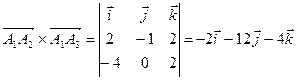
 .
.
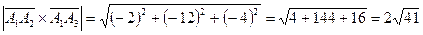 .
.
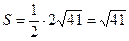 (ед2).
(ед2).
д) Объем пирамиды, построенной на векторах 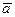 ,
, 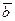 ,
, 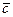 определяем с помощью смешанного произведения векторов по формуле:
определяем с помощью смешанного произведения векторов по формуле:
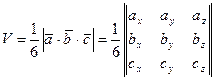 .
.
V = 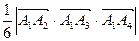 .
.
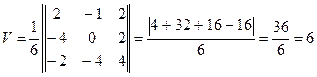 (ед3).
(ед3).
Модуль 2
Аналитическая геометрия на плоскости
и в пространстве
Задачи для решения
Задание 1
Дана кривая второго порядка. Найти ее вершины, фокусы, эксцентриситет. Для гиперболы составить уравнение асимптот. Построить кривую второго порядка.
Варианты
1. 9x2 + 16y2 = 144;
2. 4x2 – 9y2 = 36;
3. 9x2 + 25y2 = 225;
4. 16x2 – 9y2 = 144;
5. x2 +4y2 = 16;
6. 25x2 – 49y2 = 1225;
7. 16x2 +9y2 = 144;
8. 16x2 – 25y2 = 400;
9. 9x2 +4y2 = 36;
10. 25x2 – 16y2 = 400.
Задание 2
Найти вершину, ось симметрии, фокус и директрису параболы. Сделать чертеж.
Варианты
1. y = 4x2 - 8x + 7;
2. y2 – 2y +5 = 2x;
3. y = x2 +4x + 12;
4. y2 – x – 6y +17 = 0;
5. y2 + 8x – 16 = 0;
6. y2 – 10x - 2y – 19 = 0;
7. x2 +4x +6y – 20 = 0;
8. y2 – 6x + 14y + 49 = 0;
9. x2 – 6x – 4y + 29 = 0;
10. x2 + 8x + 6y + 46 = 0.
Задание 3
Даны координаты вершин пирамиды А1,А2 А3 А4.
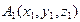 ,
, 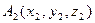 ,
, 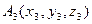 ,
, 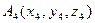 .
.
Найти:
а) уравнение ребра [A1A2];
б) уравнение грани А1А2А3;
в) угол между ребром [A1A4] и гранью А1А2А3;
г) уравнение высоты h, опущенной из вершины А4 на грань
А1А2А3;
д) длину d высоты h.
Варианты
1. А1(3,1,4), А2 (-1,6,1), А3 (-1,1,6), А4(0,4,-1);
2. А1 (3,3,9), А2 (6,9,1), А3(1,7,3), А4(8,5,8);
3. А1(3,5,4), А2 (5,8,3), А3 (1,9,9), А4(6,4,8);
4. А1 (2,4,3), А2 (7,6,3), А3 (4,9,3), А4(3,6,7);
5. А1 (9,5,5), А2 (-3,7,1), А3(5,7,8), А4(6,9,12);
6. А1 (0,7,1), А2 (4,1,5), А3 (4,6,3), А4(3,9,8);
7. А1 (5,5,4), А2 (3,8,4), А3(3,5,10), А4(5,8,2);
8. А1(6,1,1), А2(4,6,6), А3(4,2,0), А4(1,2,6);
9. А1(7,5,3), А2 (9,4,4), А3 (4,5,7), А4(7,9,6);
10. А1(6,6,2), А2(5,4,7), А3(2,4,7), А4(7,3,0).
Решение типовых задач
Задание 1
Дана кривая второго порядка. Найти ее вершины, фокусы, эксцентриситет. Для гиперболы составить уравнение асимптот. Построить кривую второго порядка.
а) 3x2 + 4y2 = 12; б) 9x2 – 16y2 = 144.
Задание 2
Найти вершину, ось симметрии, фокус и директрису параболы. Сделать чертеж.
Уравнение параболы y2 – 2x + 4y + 2 = 0.
Задание 3
Даны координаты вершин пирамиды А1 А2 А3 А4.
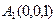 ,
, 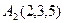 ,
, 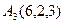 ,
, 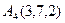 .
.
Найти:
а) уравнение ребра [A1A2];
б) уравнение грани А1А2А3;
в) угол между ребром [A1A4] и гранью А1А2А3;
г) уравнение высоты, опущенной из вершины А4 на грань А1А2А3;
д) длину высоты.
Пример выполнения задания 1
a) Дана кривая второго порядка:
3x2 + 4y2 = 12.
Это уравнение эллипса. Преобразуем его к каноническому виду 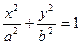 .
.
Разделим обе части уравнения на 12: 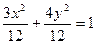 . Каноническое уравнение имеет вид:
. Каноническое уравнение имеет вид: 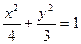 .
.
Большая полуось эллипса а = 2, а малая полуось 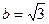 .
.
Следовательно, координаты его вершин:
А1(-2; 0), А2(2; 0), В1(0; 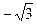 ), В2(0;
), В2(0; 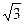 ).
).
Координаты фокусов: F1(-с; 0) ; F2(с; 0).
Найдем с по формуле: 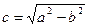 ;
; 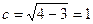 .
.
Координаты фокусов: F1(-1; 0) ; F2(1; 0).
Эксцентриситет эллипса: 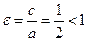 .
.
б) Дана кривая второго порядка:
9x2 – 16y2 = 144.
Это уравнение гиперболы. Преобразуем его к каноническому виду 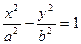 .
.
Разделим обе части уравнения на 144: 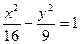 .
.
Полуоси данной гиперболы: действительная а = 4, мнимая b=3. Следовательно, ее вершины:
А1(-4;0), А2(4;0), В1(0;-3), В2(0;3).
Прямоугольник с центром в начале координат, сторонами, параллельными координатным осям и проходящими через вершины гиперболы, называется основным прямоугольником гиперболы. Его диагонали 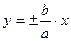 являются асимптотами гиперболы.
являются асимптотами гиперболы.
Асимптоты: 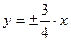 .
.
Координаты фокусов: F1(-с; 0) ; F2(с; 0).
Найдем с по формуле: 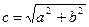 ;
; 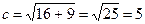 , следовательно, F1(-5;0); F2(5;0).
, следовательно, F1(-5;0); F2(5;0).
Эксцентриситет гиперболы 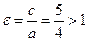 .
.
Пример выполнения задания 2
Найдём вершину, ось симметрии, фокус и директрису параболы
y2 – 2x + 4y + 2 = 0.
Приведем уравнение параболы к каноническому виду
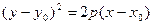 . Здесь
. Здесь 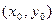 – координаты вершины,
– координаты вершины,
р – параметр параболы (расстояние между фокусом и директрисой).
Выделим в уравнении параболы полный квадрат по у:
y2 +4y + 4 – 2x – 4 + 2 = 0,
(y + 2)2 = 2x + 2.
Каноническое уравнение:
(y + 2)2 = 2(x + 1).
Координаты вершины О1(-1;-2). Парабола симметрична относительно прямой у = -2. Величина параметра р = 1.
Если вершина параболы находится в точке (0,0), то координаты её фокуса: F(p/2;0), уравнение директрисы: х = -р/2. Следовательно, наша парабола имеет фокус в точке 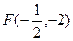 .
.
Уравнение директрисы 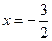 .
.
Пример выполнения задания 3
Даны координаты вершин пирамиды А1А2А3А4:
А1(0,0,1), А2 (2,3,5), А3 (6,2,3), А4(3,7,2).
а) Канонические уравнения прямой, проходящей через точки А1(х1, у1, z1) и А2(х2, у2, z2) имеют вид:
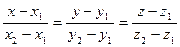 .
.
Следовательно, уравнение ребра [ 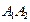 ], как уравнение прямой
], как уравнение прямой 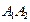 имеет вид:
имеет вид:
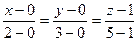 , или
, или 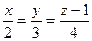 .
.
б) Составим уравнение плоскости А1А2А3 как уравнение плоскости, проходящей через три данные точки 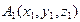 ,
, 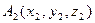 ,
, 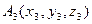 :
:
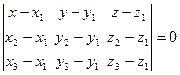 .
.
Получим:
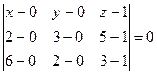 , т.е.
, т.е. 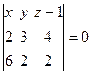 .
.
Приведём это уравнение к общему виду:
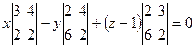 ,
,
x(6 - 8) – y(4 – 24) + (z – 1)(4 – 18) = 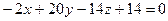 . Разделим последнее равенство на –2 и получим общее уравнение плоскости А1А2А3: x – 10y + 7z – 7 = 0.
. Разделим последнее равенство на –2 и получим общее уравнение плоскости А1А2А3: x – 10y + 7z – 7 = 0.
б) Угол между ребром [A1A4] и гранью А1А2А3 определим как угол 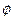 между прямой
между прямой 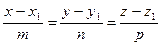 и плоскостью
и плоскостью 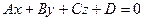 . Синус этого угла находим по формуле:
. Синус этого угла находим по формуле:
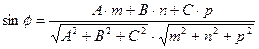 .
.
Уравнение ребра [A1A4] находим аналогично уравнению [ 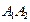 ]:
]: 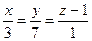 .
.
Уравнение плоскости А1А2А3: x – 10y + 7z – 7 = 0.
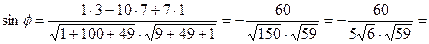
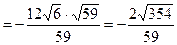 .
.
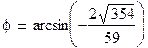 .
.
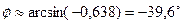 .
.
г) Составим уравнение высоты, опущенной из вершины А4 на грань А1А2А3, как уравнения прямой, проходящей через точку А4:
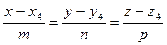 , перпендикулярно плоскости А1А2А3
, перпендикулярно плоскости А1А2А3 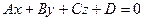 .
.
Для нахождения m, n, p используем условие перпендикулярности прямой и плоскости 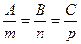 .
.
Уравнение прямой: 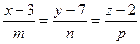 .
.
Уравнение плоскости: x – 10y + 7z – 7 = 0.
Так как А = 1, В = -10, С = 7, то m = 1, n = -10, p = 7.
Следовательно, уравнение высоты имеет вид:
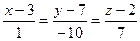 .
.
 д) Длину высоты определим по формуле для вычисления расстояния d от точки
д) Длину высоты определим по формуле для вычисления расстояния d от точки 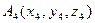 до плоскости А1А2А3
до плоскости А1А2А3 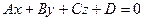 .
.
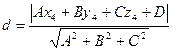 .
.
Координаты точки А4(3,7,2).
Уравнение плоскости А1А2А3: x – 10y + 7z – 7 = 0.
Следовательно,
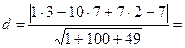
= 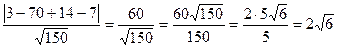 .
.
Модуль 3
Введение в математический анализ. Дифференциальное исчисление функций одной переменной
Задачи для решения
Задание 1
С помощью подходящих алгебраических преобразований или использования известных (замечательных) пределов найти пределы функций.
Варианты
1. а) 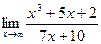 ; 2. а)
; 2. а) 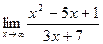 ;
;
б) 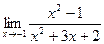 ; б)
; б) 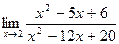 ;
;
в) 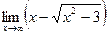 ; в)
; в) 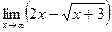 ;
;
г) 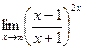 ; г)
; г) 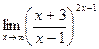 ;
;
д) 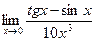 . д)
. д) 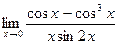 .
.
3. а) 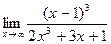 ; 4. а)
; 4. а) 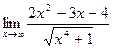 ;
;
б) 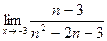 ; б)
; б) 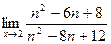 ;
;
в) 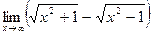 ; в)
; в) 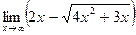 ;
;
г) 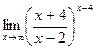 ; г)
; г) 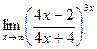 ;
;
д) 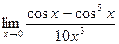 . д)
. д) 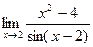 .
.
5. а) 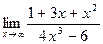 ; 6. а)
; 6. а) 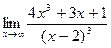 ;
;
б) 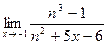 ; б)
; б) 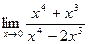 ;
;
в) 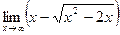 ; в)
; в) 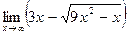 ;
;
г) 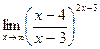 ; г)
; г) 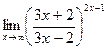 ;
;
д) 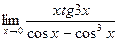 . д)
. д) 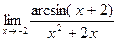 .
.
7. а) 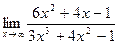 ; 8. а)
; 8. а) 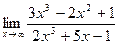 ;
;
б) 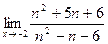 ; б)
; б) 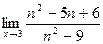 ;
;
в) 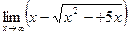 ; в)
; в) 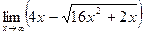 ;
;
г) 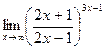 ; г)
; г) 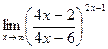 ;
;
д) 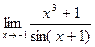 . д)
. д) 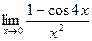 .
.
9. а) 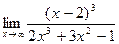 ; 10. а)
; 10. а) 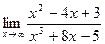 ;
;
б) 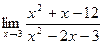 ; б)
; б) 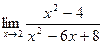 ;
;
в) 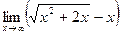 ; в)
; в) 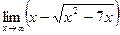 ;
;
г) 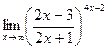 ; г)
; г) 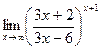 ;
;
д) 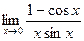 . д)
. д) 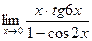 .
.
Задание 2
Найти производные первого порядка указанных функций:
Варианты
1. а) 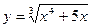 ; б)
; б) 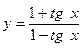 ; в) y = x · arcsin23x;
; в) y = x · arcsin23x;
г) 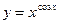 ; д) xsin y – y ·cos x = 0; е)
; д) xsin y – y ·cos x = 0; е) 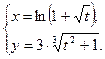
2. a) 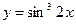 ; б)
; б) 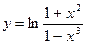 ; в)
; в) 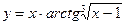 ;
;
г) 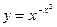 ; д) у sin х – cos( x - у) = 0; е)
; д) у sin х – cos( x - у) = 0; е) 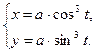
3 . a) 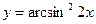 ; б)
; б) 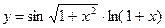 ;
;
в) 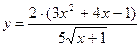 ; г)
; г) 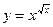 ;
;
д) 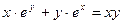 ; е)
; е) 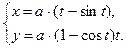
4. a) 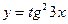 ; б)
; б) 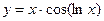 ; в)
; в) 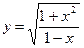 ;
;
г) 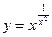 ; д)
; д) 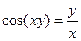 ; е)
; е) 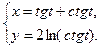
5. a) 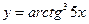 ; б)
; б) 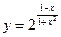 ; в)
; в) 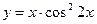 ;
;
г) 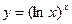 ; д)
; д) 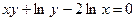 ;
;
е) 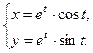
6. а) 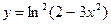 ; б)
; б) 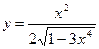 ; в)
; в) 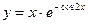 ;
;
г) 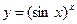 ; д)
; д) 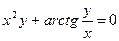 ; е)
; е) 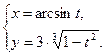 .
.
7. а) 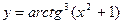 ; б)
; б) 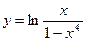 ;
;
в) 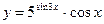 ; г)
; г) 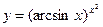 ;
;
д) 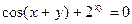 ; е)
; е) 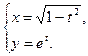
8. а) 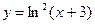 ; б)
; б) 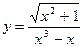 ;
;
в) 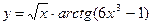 ; г)
; г) 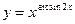 ;
;
д) 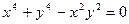 ; е)
; е) 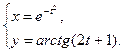
9. а) 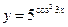 ; б)
; б) 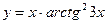 ; в)
; в) 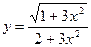 ;
;
г) 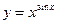 ; д)
; д) 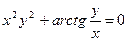 ; е)
; е) 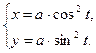
10. а) 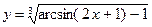 ; б)
; б) 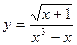 ;
;
в) 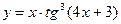 ; г)
; г) 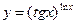 ;
;
д) 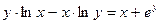 ; е)
; е) 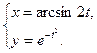
Задание 3
Найти дифференциал второго порядка указанных функций.
Варианты
1. y = arctg2х ; 2. 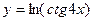 ;
;
3. 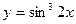 ; 4.
; 4. 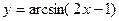 ;
;
5. 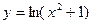 ; 6.
; 6. 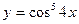 ;
;
7. 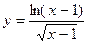 ; 8.
; 8. 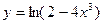 ;
;
9. y = 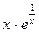 ; 10.
; 10. 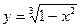
Задание 4
Произвести общее исследование функции, выявить присущие ей характерные точки, линии и области и по ним построить ее график.
Варианты
1. 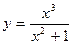 ; 2.
; 2. 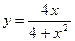 ;
;
3. 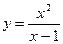 ; 4.
; 4. 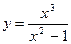 ;
;
5. 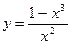 ; 6.
; 6. 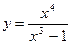 ;
;
7. 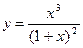 ; 8.
; 8. 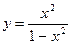 ;
;
9. 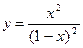 ; 10.
; 10. 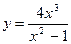 .
.
Задание 5
Найти значение выражения.
Варианты.
1. 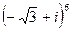 ; 2.
; 2. 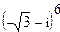 ;
;
3. 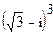 ; 4.
; 4. 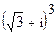 ;
;
5. 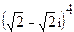 ; 6.
; 6. 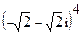 ;
;
7. 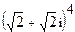 ; 8.
; 8. 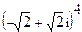 ;
;
9. 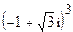 ; 10.
; 10. 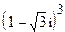 .
.
Решение типовых задач
Задание 1
С помощью подходящих алгебраических преобразований или использования известных (замечательных) пределов функций найти пределы функций.
а) 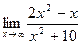 ; б)
; б) 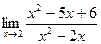 ;
;
в) 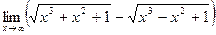 ;
;
г) 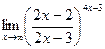 ; д)
; д) 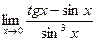 .
.
Задание 2
Найти производные первого порядка указанных функций.
а) 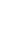 у = arcsin2(ex); б)
у = arcsin2(ex); б) 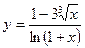 ; в)
; в) 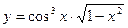 ; г)
; г) 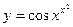 ; д) x3y2 + 5xy + 4 = 0; е)
; д) x3y2 + 5xy + 4 = 0; е) 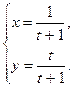
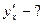
Задание 3
Найти дифференциал второго порядка функции у = ln(cos(5x)).
Задание 4
Произвести общее исследование функции 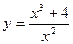 , выявить присущие ей характерные точки, линии и области и по ним построить ее график.
, выявить присущие ей характерные точки, линии и области и по ним построить ее график.
Задание 5
Выполнить над комплексными числами указанные действия:
а) 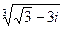 ; б)
; б) 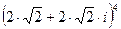 .
.
Сведения из теории
Определение предела функции
Число А называется пределом функции y = f(x) при x стремящемуся к а, если для любого сколь угодно малого положительного числа эпсилон (ε >0) найдется такое число δ (дельта), величина которого зависит от ε (δ(ε) > 0), что при всех x ≠ a и удовлетворяющих неравенству 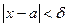 выполняется неравенство |f(x)-A| < ε. В этом случае пишут :
выполняется неравенство |f(x)-A| < ε. В этом случае пишут : 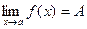 .
.
Если x →a и при этом x<a, то пишут х →a – 0.
Если x →a и при этом x >a, то пишут x → a+0.
Предел 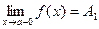 называется левосторонним.
называется левосторонним.
Предел 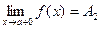 называется правосторонним.
называется правосторонним.
Число А называется пределом функции y = f(x) при х стремящемся к ∞, если для любого малого положительного числа ε (ε > 0) существует такое положительное число М, величина которого зависит от ε (М(ε) > 0), что для всех значений х, удовлетворяющих неравенству |x| > М(ε), будет выполняться неравенство |f(x)-A| < ε. В этом случае пишут 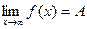 .
.
При вычислении пределов функций необходимо знать следующие теоремы:
1. 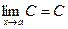 , где С – постоянная.
, где С – постоянная.
2. 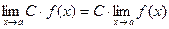 , где С – постоянная.
, где С – постоянная.
3. Если 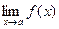 и
и 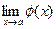 существуют, то
существуют, то
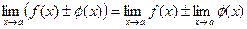 .
.
4. 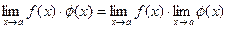 .
.
5. 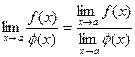 , если
, если 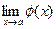 ≠ 0.
≠ 0.
Они справедливы как для пределов числовых последовательностей, так и для пределов функций. Перечисленные свойства справедливы как для x→a, так и для x→ ∞.
