Построение разверток пирамидальных и конических поверхностей.

1. Выполнить комплексный чертеж наклонной треугольной пирамиды и построить ее развертку.

2. Ответить на следующие вопросы:

а) какие поверхности называются неразвертывающимися;

б) что называется разверткой поверхности;

в) какие поверхности относятся к числу развертывающихся;

г) как строится развертка наклонного эллиптического конуса;

Пример 1. Построить развертку боковой поверхности наклонной треугольной пирамиды SABC (рис. 12.2)

Развертку боковой поверхности пирамиды строим по следующей схеме:

1. Определяем длины ребер и сторон основания пирамиды.

2. Строим на плоскости чертежа последовательно по трем сторонам
треугольники (грани пирамиды), примыкающие друг к другу и с общей
вершиной.

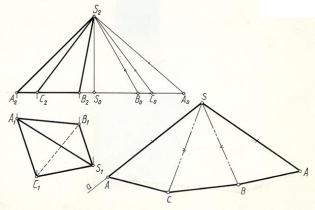
Решение. Как видно из чертежа, основание ABC пирамиды расположено в горизонтальной плоскости и поэтому его стороны на П₁ проецируются в натуральную величину. Натуральные размеры боковых ребер определяем с помощью прямоугольных треугольников, у которых одним катетом является превышение точки S над точками А, В, С (отрезок S₂S₀), a вторым катетом отрезок, равный горизонтальной проекции соответствующего бокового ребра (S₀A₀=S₁A₁, S₀B₀=S₁B₁, S₀C₀= S₁C₁). Натуральной величиной боковых ребер являются отрезки S₂A₀, S₂B₀, S₂C₀. После определения натуральных величин ребер приступаем к построению развертки. Для этого из произвольной точки S проводим произвольную прямую а. Откладываем на ней от точки S-SA=S₂A₀. Из точки А проводим дугу радиусом A₁C₁,а из точки S-дугу радиусом S₂C₀.Пересечение дуг определяет положение вершины В треугольника SАВ-натуральной величины грани пирамиды. Аналогично находим точки B и А. Соединив точки А С В A S, получим развертку боковой поверхности пирамиды SABC.

Пример 2. Построить развертку боковой поверхности наклонного эллиптического конуса с круговым основанием

Развертка конической поверхности выполняется по схеме построения развертки боковой поверхности пирамиды, способу треугольников. Для этого коническая поверхность аппроксимируется (заменяется) вписанной в нее многогранной пирамидальной поверхностью.

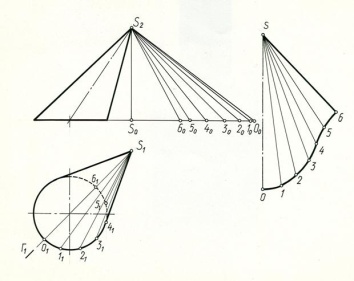
Решение. В данную коническую поверхность впишем двенадцатиугольную пирамиду. Так как коническая поверхность имеет плоскость симметрии Г, то можно построить развертку только одной половины поверхности. Разделим половину окружности на 6 равных частей, начиная от точки (O₁) пересечения ее с плоскостью симметрии Г (Г₁), которая делит поверхность и, следовательно, ее развертку на 2 симметричные части. Через точки деления O₁l₁, 2₁ ... и вершину S₁ проводим горизонтальные проекции образующих конуса- прямые S₁O₁, S₁1₁, S₁2₁ ..., которые являются боковыми ребрами вписанной пирамиды. Сторонами основания пирамиды являются хорды, соединяющие точки деления и проецирующиеся на П₁ в натуральную величину. Натуральную величину боковых ребер определяем способом прямоугольных треугольников. Проводим ось симметрии развертки и от точки S откладываем отрезок SO=S₂О₀ (pиc. 11.3). Из точки S радиусом S₂1₀ проводим дугу окружности, а из точки О радиусом О₁1₁делаем на ней засечку. Точка 1 – искомая точка развертки. Для построения смежной грани из точки S радиусом S₂2₀, а из точки 1 радиусом 1₁2₁ сделаем засечки и в пересечении отметим точку 2 и т.д. Соединив точки 0,1, 2 ... 6 плавной кривой получим развертку ½ боковой поверхности конуса.

Экзаменационный билет №_25

Построение разверток призматических и цилиндрических поверхностей.

1. Выполнить комплексный чертеж наклонной треугольной призмы и построить ее развертку;

2. Ответить на следующие вопросы:

а) какие поверхности называются развертывающимися;

б) что называется разверткой;

в) какие поверхности относятся к числу развертывающихся;

г) к чему сводится построение развертки наклонного эллиптического цилиндра.

Пример 1. Построить полную развёртку поверхности треугольной призмы и нанести на ней точку М, принадлежащую поверхности.

Призма расположена таким образом, что её боковые ребра являются горизонталями, следовательно на виде сверху они имеют натуральную величину.

Чтобы построить «нормальное» сечение проведём вертикальную плоскость Б перпендикулярно к боковым ребрам призмы. Построим натуру сечения с помощью дополнительного вида, выполненного по направлению горизонтали, перпендикулярной к плоскости Б. Стороны треугольника натурального вида сечения будут являться искомыми высотами параллелограммов.

Т.к. при построении развёртки углы и параллельности сохраняются, то на развёртке боковые ребра будут параллельны между собой и перпендикулярны прямой линии, в которую развернётся «нормальное» сечение.

Построение развёртки начинается с проведения прямой линии, на которой откладываем длины сторон нормального сечения (высоты параллелограммов) 1-2, 2-3, 3-1.

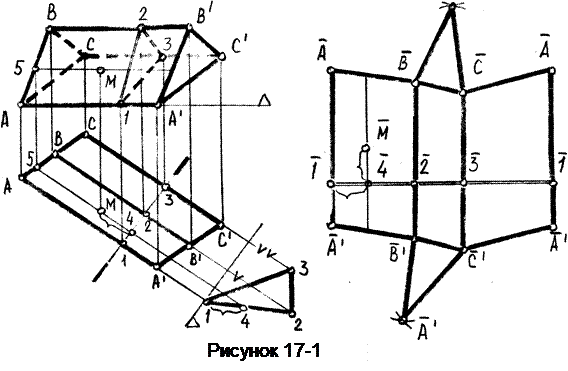
Через концы этих сторон проведём прямые перпендикулярные им. На полученных перпендикулярах отложим отрезки боковых рёбер, измеренные на виде сверху относительно нормального сечения. Соединив между собой полученные точки отрезками прямых, получим развёртку боковой поверхности призмы. Присоединив к этой развёртке оба основания, получим полную развёртку поверхности призмы.

Чтобы построить на развёртке точку М, принадлежащую поверхности призмы, необходимо найти на развёртке положение прямой, на которой эта точка лежит. Для этого найдём точку пересечения этой прямой с плоскостью Б на натуральном виде сечения. Замерим расстояние 1-4 и отложим его на развёртке. Через полученную точку проведём прямую, параллельную ребрам призмы. Затем измерим на виде сверху длину отрезка - от нормального сечения до точки М и отложим его на развёртке.

Экзаменационный билет №_26