Установка и методика измерения отношений

Установка для проведения опыта показана на рисунке 2.

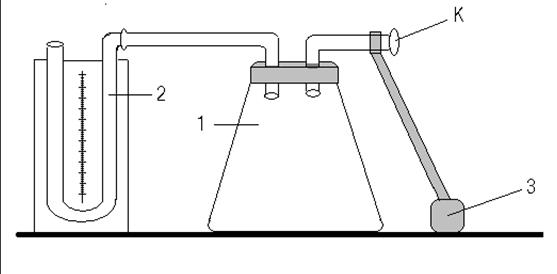
Рис. 2. Установка для определения γметодом адиабатического расширения: 1 – стеклянный сосуд, 2 – манометр, 3 – резиновая груша, К – трехходовой кран.

Большой стеклянный сосуд (баллон) постоянно соединен с открытым водяным манометром. Через трехходовой кран К к баллону подведена резиновая груша. Кран имеет три рабочих положения: «насос-баллон», «баллон-атмосфера» и «закрыто». Обозначим их условно 1, 2 и 3, соответственно. В положении 2 в баллоне устанавливается давление Р и температура Т, равные комнатным. Выделим мысленно внутри сосуда некоторую массу объемом V₀. Поставим кран в положение 1, накачаем в баллон немного воздуха и закроем его, установив ручку в положение 3. При этом объем выделенной массы уменьшится, а температура повысится. Подождем, пока температура газа станет равной комнатной. Тогда выделенная масса газа будет иметь параметры Р₁, V₁, Т₀. На диаграмме (рис. 3) это состояние обозначено цифрой 1. Откроем кран (К-3) так, чтобы давление в баллоне сравнялось с атмосферным, и снова закроем (К-2). Так как время установления равновесий давлений немного меньше соответствующего времени для температур, то процесс расширения газа в сосуде можно считать адиабатическим. Обозначим состояние выделенной массы газа после этого процесса Р₀, V₂, Т₂. На рис. 3 это состояние обозначено цифрой 2. При адиабатическом расширении газ охладился. После того, как кран закрыли (К-3), происходит постепенное нагревание газа до комнатной температуры, и давление возрастает. Конечное состояние газа 3 имеет параметры Р₂, V₂, Т₀. Состояния 2 и 1 связаны уравнением Пуассона PV^γ = const, а состояния 1 и 3 – уравнением Бойля - Мариотта PV = const. То есть можно записать:

3 – 1: PV = const (10)

2 – 1: PV^γ = const.

Р

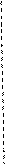
Р₁ 1

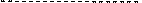Р₂ 3

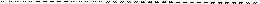Р₀ 2 0

V₁ V₂ V₀ V

Рис. 3. Диаграмма состояния: 1 – первоначальное состояние, 2 – состояние после адиабатического расширения из точки 1, 3 – состояние после изохорного нагрева из точки 2.

Давление газа выражается через разность уравнений жидкости в трубах манометра следующим образом:

Р₁ = Р_о +ρ g Δh₁ , (11)

P₂ = P_o + ρ g Δh₂,

где ρ – плотность жидкости в манометре.

Продифференцируем (10) для перехода 3 – 1:

pdV + VdP = 0

или, с учетом изменения параметров:

P (V₂ - V₁) + V (P₂ - P₁) = 0 (12)

Продифференцируем (6) для перехода 2 – 1:

γ PdV + VdP = 0,

γ P(V₂ - V₁) + V (P₀ - P₁) = 0. (13)

Выразим из (12):

P (V₂ - V₁) = V (P₁ - P₂)

И подставим в (13):

γ V (P₁ - P₂) + V (P₀ - P₁) = 0.

Отсюда:

γ = (Р₁ - Р₀)/(Р₁ - Р₂)(14)

Что с учетом (11) дает:

γ = Δh₁/( Δh₁ – Δh₂)(15)

Описанный метод дает не совсем точное значение γпо следующим причинам:

1. В воздухе всегда присутствуют водяные пары, которые не только понижают степень идеальности газа, но и состоят из молекул Н₂О с шестью, а не с пятью степенями свободы.

2. Процесс расширения лишь весьма приближенно можно считать адиабатическим.

3. Если кран после адиабатического расширения закрыть с опозданием, то успевает начаться его изобарический нагрев.

Порядок выполнения работы

1. Поставить кран в положение 1 (K-1) и накачивать воздух в баллон до тех пор, пока разность уровней в манометре не достигнет 20 - 25 см. Закрыть кран (К-2).

2. Подождать 30 - 40 секунд, пока давление в манометре не установится на стационарном уровне, после чего записать значение разнос­ти уровней Δh₁. (Если давление продолжает все время понижаться, то в установке имеется течь, которую необходимо устранить).

3. Краном соединить баллон с атмосферой (К-3) и, как только дав­ление газа в баллоне станет равным атмосферному, сразу же поста­вить кран в положение «закрыто» (К-3). (Здесь надо выпускать из баллона воздух лишь 2 - 3 секунды и закрыть кран сразу же после прекращения шипения выходящего воздуха).

4. Подождать 3 - 4 минуты, пока в баллоне установится равновесное давление (тем­пература станет равной комнатной) и записать разность уравнений манометра Δh_2.

5. Повторить измерения 10 раз, изменяя величину Δh_1. Результаты занести в таблицу 1.

Таблица 1.

Δh1
Δh2
γ
γист

Используя формулу (15), вычислить значения γ для каждого случая, затем найти ее среднее значение и оценить погрешность σ.

5.Контрольные вопросы

1. Дать общее определение теплоемкости, удельной и молярной теплоемкости.

2. Чему равна теплоемкость воздуха при изохорическом и изобаричес­ком процессах, если считать его идеальным газом, в котором от­сутствуют водяные пары?

3. Какой процесс называется адиабатическим? Из математического выражения для первого начала термодинамики и уравнения состояния идеального газа выведите уравнение Пуассона.

4. Прокомментируйте процессы, происходящие в эксперименте и изображенные на рис. 3. Выведите рабочую формулу (15).

5. Изобразите происходящие в эксперименте процессы в координатах:
а) Р,Т,

б) V, Т.

6. Напишите уравнение Пуассона для смеси нескольких идеальных газов, отличающихся по молекулярному весу и количеству атомов в молеку­ле.

7. Чему равна работа, совершаемая газом при его адиабатическом расширении? Выведите формулу и подсчитайте, как относятся величины совершае­мой работы для одно-, двух-, трехатомного газа.

8. Что называется политропическим процессом? Выведите его уравнение
(уравнение политропы); получите из него уравнение адиабаты.

9. В каких пределах может меняться показатель политропы для двухатомного идеального газа?

10. Пусть имеются одно-, двух-, трехатомные идеальные газы, участвую­щие в различных политропических процессах, характеризующихся од­ной и той же теплоемкостью С. Как соотносятся между собой их показатели политропы? Предварительно выведите, чему равна теплоемкость идеального газа, участвующего в процессе, описываемом уравнением политропы.

ЛАБОРАТОРНАЯ РАБОТА 1-4