Пределение излучательной способности вольфрамовой проволоки.

абораторная работа №3

по курсу «Тепломассообмен»

пределение излучательной способности вольфрамовой проволоки.

Выполнил:	студент группы АТП-10 Гончаров А.В.
Преподаватель:	Шевцова С.Б.

Волжский 2012

Цель работы: изучение теории лучистого теплообмена, его законов, факторов, влияющих на интенсивность процесса теплового излучения.

Теоретические основы работы

Суммарное излучение с поверхности по всем длинам волн спектра называется интегральным или полным потоком излучения.

Интегральный поток, испускаемый с единицы поверхности, носит название поверхностной плотности потока интегрального излучения:

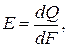
(3.1)

где dQ – излучательный поток, испускаемый элементарной площадкой dF, Вт.

Лучистый поток со всей поверхности выразится:

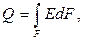
(3.2)

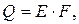Если плотность интегрального излучения для всех элементов поверхности излучаемого тела одинакова, то зависимость (3.2) переходит в соотношение:

(3.3)

Излучение, которое определяется природой данного тела и его температурой, называется собственным излучением.

Обычно тело участвует в лучистом теплообмене с другими телами. Энергия излучения других тел, попадая на поверхность данного тела извне, частично поглощается, частично отражается, а часть её проходит сквозь тело. Количество лучистой энергии, падающее на данное тело в поле излучения, обозначается:

Q_пад или Е_пад

Часть падающей энергии излучения, поглощенной данным телом, называется потоком поглощенного излучения.

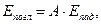При поглощении лучистая энергия вновь превращается во внутреннюю энергию:

(3.4)

где А – интегральная поглощающая способность тела.

При А = 1 – тело абсолютно черное.

Тела, для которых поглощательная способность не зависит от длины волны, называются серыми телами:

А_l = const £ 1;

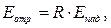Часть энергии, которую поверхность данного тела отражает обратно, носит название потока отраженного излучения.

(3.5)

где R – интегральная отражательная способность тела.

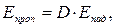Часть энергии, проходящей сквозь тело, называется плотностью потока пропускаемого излучения.

(3.6)

где D – интегральная пропускная способность тела.

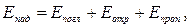Для тела, участвующего в лучистом теплообмене с другими телами, согласно закону сохранения энергии можно составить уравнения теплового баланса:

(3.7)

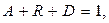или

(3.8)

Если поделить на 1/Е_пад, лучистый теплообмен между телами определяется потоком результирующего излучения.

Рисунок 1

Результирующий поток может быть найден разными способами:

1 способ (способ Нуссельта):

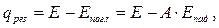по (а-а), с учетом Е_проп = 0;

(3.9)

2 способ (способ О. Е. Власова):

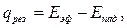по (б-б);

(3.10)

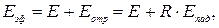
где Е_эф – плотность эффективного излучения.

3 способ (способ Ю. Н. Суринова):

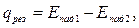по (в-в);

(3.11)

По закону Стефана – Больцмана, устанавливающего зависимость плотности потока излучения от температуры:

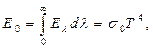
(3.12)

где s₀ – постоянная Стефана – Больцмана.

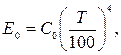Для удобства практических расчетов:

(3.13)

где С₀ = 5,67 – коэффициент излучения абсолютно черного тела, Вт/(м²∙К⁴).

Для серых тел закон Стефана – Больцмана примет вид:

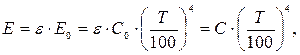
(3.14)

где 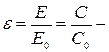интегральная степень черноты серого тела;

С – его коэффициент излучения, Вт/(м²∙К⁴).

Для определения результирующих потоков излучения необходимо располагать данными по коэффициентам излучения. Коэффициент излучения является сложной функцией, зависящей от природы излучающего тела, его температуры, состояния поверхности и т.д.

Поглощающая способность зависит от тех же факторов, от которых зависит степень черноты. Кроме того, она зависит от природы падающего излучения. Поэтому непосредственно измеренная величина степени черноты может отличаться от непосредственно измеренной величины поглощательной способности для того же тела при одинаковых условиях.

Обычно измеряется относительный коэффициент излучения, так как непосредственное измерение поглощательной способности связано со значительными трудностями.

Опытное исследование интегральных коэффициентов излучения твердых тел может быть проведено следующими методами: радиационным, калориметрическим, методом регулярного режима и методом непрерывного нагревания с постоянной скоростью. Во всех методах перенос тепла за счет теплопроводности и конвекции пренебрежительно мал по сравнению с излучением.

Калориметрический метод основан на непосредственном измерении потока результирующего излучения, поэтому он относится к абсолютным методам:

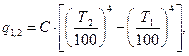
(3.15)

где Т₂ – температура исследуемого тела, К;

Т₁ – температура стенки калориметра, К.

Схема и описание установки

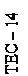
Рисунок 2 Схема экспериментальной установки

Исследуемая тонкая проволока 1 из вольфрама помещается по оси цилиндрического стеклянного сосуда (калориметра) 2. Концы проволоки впаиваются в стенки сосуда. Проволока нагревается посредством пропускания через неё электрического тока от регулируемого источника питания 4 ТЕС – 14. Вследствие этого температура проволоки может изменяться в широких пределах.

Калориметр выполнен с двойными стенками, между которыми находится термостатирующая жидкость (дистиллированная вода). Вследствие большой теплоемкости воды, её температура, а следовательно и температура стенки сосуда, практически не изменяется за время опыта и её можно принять за температуру в помещении лаборатории. Проволока передает теплоту стенкам калориметра только излучением, так как передача путем конвекции и теплопроводности пренебрежительно мала. Тепловой поток определяется по падению напряжения на измерительном участке и силе тока в нем. Падение напряжения измеряется цифровым вольтметром 3 через усилитель напряжения 5. Силу тока, проходящего через проволоку, определяют с помощью образцового сопротивления 6, включенного в схему. Падение напряжения на образцовом сопротивлении измеряется с помощью того же цифрового вольтметра 3. На измерительном участке температура проволоки практически постоянна по длине. Эта температура определяется по зависимости электрического сопротивления проволоки от температуры. Такой измерительный преобразователь температуры носит название термометра сопротивления.

Данные установки

Диаметр проволоки	– d = 0,15 мм;
Длина измерительного участка	– l = 250 мм;
Сопротивление проволоки при Т = 273 К	– R0 = 0,78 Ом;
Сопротивление образцовой катушки	– Rобр = 0,1 Ом.

Порядок выполнения работы

1. Включить установку.
2. Тумблером «сеть» включить модуль.
3. Убедиться, что ручки регулятора напряжения источника питания находятся в крайнем левом положении, а ручки регулятора силы тока – не трогать.
4. Включить источник питания.
5. Вращая ручки регулятора напряжения выставить первое значение подаваемого напряжения на нить (U_н » 1,5 В).
6. Переключить тумблер в положение U_r, при этом вольтметр покажет значение напряжения на образцовом сопротивлении, пропорциональное силе тока, проходящего через нить.
7. Дать выдержку в течении 2 – 3 минут.
8. Записать показания U_r.
9. Переключить тумблер в положение U_н.
10. Записать показания U_н.
11. Пункты 5 – 10 повторить для следующих значений напряжения на нити.
12. В опытах U_н = 1,5 ¸ 4,0 В.

Таблица результатов измерений

Напряжение	№ опытов
Uн, В	1,5	2,0	2,5	3,0	4,0
Ur, В	0,054	0,063	0,072	0,080	0,096

Таблица результатов расчета

№ опыта	Iн, А	Rн, Ом	Тн, К	Тст, К	q, Вт/м2	Q, Вт	Р, Вт/м2	e
	0,54	2,78	807,2			0,81		0,86
	0,63	3,17	911,4		1,26		0,904
	0,72	3,47	991,5		1,80		0,889
	0,80	3,75	1066,3		2,40		0,893
	0,96	4,17	1178,4		3,84		0,835

Расчет

1. Определим силу тока в нити:

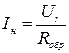
1. Определим сопротивление нити:

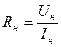
1. Определим температуру нити:

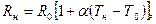
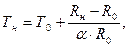
где Т₀ = 273 К;

a = 4,8∙10^-3 К^-1.

1. Рассчитаем мощность излучения для модели абсолютно черного тела:

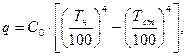
где Т_ст = Т₀ + t_ст = 273 + 20 = 293 К.

1. Определим полную мощность выделяемую нитью:

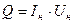
1. Определим действительную вводимую мощность с единицы поверхности:

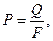
где F = p∙d∙l

1. Определим интегральную степень черноты:

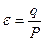
1. Построим график зависимости e = e(Т_н).

Оценка погрешностей измерения

Погрешность вычисления величины e определим по формуле:

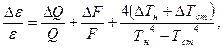где

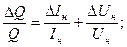
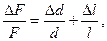
ΔI = 0,02 A; ΔU = 0,1 B; Δd = 0,01 мм; Δl = 0,5 мм; ΔТ = 0,1 К.

Произведем определение погрешности по пятому опыту.

Запишем окончательный результат с учетом погрешности.

График зависимости e = e(Т_н)