Rectangular and polar coordinates
Elements of analytical geometry
Coordinates on a line. Dividing a segment in a given ratio.A point M of the coordinate axis Ox having the abscissa x is denoted by M(x). The distance d between points M1(x1) and M2(x2) of the axis is defined as: d = |x2 – x1|.
Let AB be a segment on an arbitrary line (A – the beginning of the segment, B – its end); then every third point C of this line divides the segment ABin some ratio l where l = ± |AC| : |CB|. (l = |AC| : |CB| if the segments AC and CB are directed to the same side, and l = –|AC| : |CB| if otherwise).
If A and B lie on the axis Ox then the coordinate of a point C(x) dividing the segment between points A(x1) and B(x2) in ratio l is defined by: 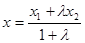 .
.
In particular, for l = 1 we obtain the formula for the coordinate of middle of a segment: 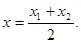
Example. The segment AB is divided on five equal parts by four points. Determine the coordinate of the closest to A point of dividing if A(-3), B(7).
Solution. Let C(x) be the required point; then l = |AC| : |CB| = ¼. Consequently, 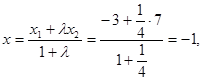 i.e. C(-1).
i.e. C(-1).
Rectangular coordinates on plane. If a rectangular Cartesian system of coordinates xOy be given on the plane then a point M of the plane having the coordinates x and y is denoted by M(x; y).
The distance between points M1(x1; y1) and M2(x2; y2) is determined as:
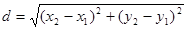 .
.
In particular, the distance d of a point M(x; y) from the origin of coordinates:
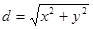 .
.
The coordinates of a point C(x; y) dividing the segment between points A(x1; y1) and B(x2; y2) in a given ratio l are determined as: 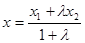 ;
; 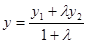 .
.
In particular, for l = 1 we obtain the formulas for coordinates of middle of a segment: 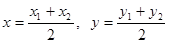 .
.
Example. Find the distance between points A(3; 8) and B(-5; 14).
Solution: 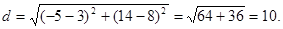
Polar coordinates. In the polar system of coordinates the position of a point M on the plane is determined by its distance |OM| = r from the pole O (r – polar radius vector of a point) and the angle q formed by the segment OM with the polar axis Ox (q - polar angle of a point). The angle q is considered to be positive from the polar axis Ox in anticlockwise direction.
If a point M has the polar coordinates r > 0 and 0 £ q < 2p then there are infinitely many pairs of polar coordinates (r; q + 2kp) where k Î Z coinciding with the position of M.
If we combine the origin of the rectangular system of coordinates with the pole, and the axis Ox – with the polar axis then the rectangular coordinates x and y of a point M and its polar coordinates r and q are linkedby the following formulas: 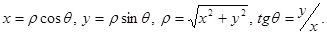
Example. Find the polar coordinates of 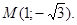
Solution: 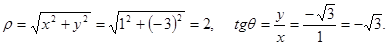 Obviously the point M lies in the IV quarter and consequently
Obviously the point M lies in the IV quarter and consequently 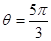 . Thus,
. Thus, 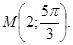
Example. Find the rectangular coordinates of 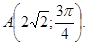
Solution: 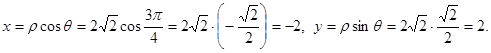 Thus, we have: A(-2; 2).
Thus, we have: A(-2; 2).
Parametric equations of a line. For finding an equation of a set of points sometimes it turns out more convenient to express the coordinates x and y of an arbitrary point of the set by some auxiliary quantity t (it is called a parameter), i.e. to consider a system of equations x = j(t), y = y(t). Such a representation of the required line is called parametric, and the equations of the system – parametric equations of the given line.
An exclusion of parameter t from a system (if it is possible) reduces to an equation connecting x and y.
Example. Which line is determined by parametric equations x = t2, y= t2?
Solution: Excluding the parameter t, we come to the equation y = x. By the parametric equations we have: x ³ 0, y ³ 0. Consequently, the given parametric equations determine a ray – the bisectrix of the first coordinate angle.
Straight line (line)
Common equation of a line.Every equation of the first order with regard to x and y, i.e. an equation Ax + By + C = 0 (where A, B and C are constant coefficients, and A2 + B2 ¹ 0) determines some (straight) line of the plane. It is called a common equation of a line.
Equation of a line with slope (slope-intercept form of the equation of a line). If B ¹ 0 in a common equation of a line then expressing it by y we obtain y = kx + b (where k = – A/B, b = – C/B). It is called an equation of a line with slope because k = tg a where a is the angle formed by the straight line with the positive direction of Ox. The constant term b of the equation equals the ordinate of the point of intersection of the line with the axis Oy.
Equation of a line in segments. If C ¹ 0 in a common equation of a line then dividing all its terms on (-C) we obtain 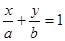 (here a = – C/A, b = – C/B). It is an equation of a line in segments; a is the abscissa of the point of intersection of the line with the axis Ox, and b – the ordinate of the point of intersection of the line with the axis Oy. Therefore a and b are called segments of the line on the coordinate axes.
(here a = – C/A, b = – C/B). It is an equation of a line in segments; a is the abscissa of the point of intersection of the line with the axis Ox, and b – the ordinate of the point of intersection of the line with the axis Oy. Therefore a and b are called segments of the line on the coordinate axes.
Normal equation of a line.If we multiply both parts of a common equation of a line Ax + By + C = 0 on the number 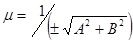 (which is called the normalizing multiplier) and choose a sign before the radical so that the condition mC < 0 holds then we obtain x cosj + y sinj – p = 0. It is a normal equation of a line. Here p is the length of the perpendicular dropped from the origin of coordinates on the line, and j is the angle formed by the perpendicular with positive direction of the axis Ox.
(which is called the normalizing multiplier) and choose a sign before the radical so that the condition mC < 0 holds then we obtain x cosj + y sinj – p = 0. It is a normal equation of a line. Here p is the length of the perpendicular dropped from the origin of coordinates on the line, and j is the angle formed by the perpendicular with positive direction of the axis Ox.
Example. Let a common equation of a line be given: 12x – 5y – 65 = 0. Write:
1) equation with a slope; 2) equation in segments; 3) normal equation.
Solution: 1) Express the equation with regard to y. Then we obtain an equation with a slope: y = (12/5)x – 13 (here k = 12/5, b = - 13).
2) Move the constant term of the common equation to the right part and divide both parts on 65; we have (12/5)x – (5/65)y = 1. Rewriting the last equation in the following form: 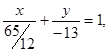 we obtain an equation in segments (here a = 65/12, b = -13).
we obtain an equation in segments (here a = 65/12, b = -13).
3) Find the normalizing multiplier 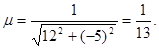 Multiplying both parts of the common equation on m, we obtain the normal equation of the line
Multiplying both parts of the common equation on m, we obtain the normal equation of the line 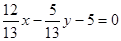 (here cosj = 12/13, sinj = -5/13, p = 5).
(here cosj = 12/13, sinj = -5/13, p = 5).
An angle between lines. An equation of a line passing through two points. The acute angle between lines y = k1x + b1 and y = k2x + b2 is determined as:
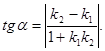
The condition of parallelism of lines: k1 = k2.
The condition of perpendicularity of lines: k1 = –1/k2.
The equation of a line having the slope k and passing through M(x1; y1) is written as: y – y1 = k(x – x1).
The equation of a line passing through M1(x1; y1) and M2(x2; y2):
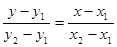
and the slope of the line is founded by: 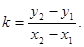
If x1 = x2 then the equation of a line passing through M1 and M2: x = x1.
If y1 = y2 then the equation of a line passing through M1 and M2: y = y1.
The distance between the point M (x0, y0) and the line Ax + By + C = 0 is determined by the formula: 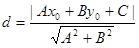
Example. Determine the acute angle between the lines y = –3x + 7 and y = 2x + 1.
Solution: Assuming k1 = -3, k2 = 2, we obtain 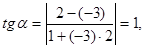 i.e.j = p/4.
i.e.j = p/4.
Example. Compose the equation of a line passing through M(-1; 3) and N(2; 5).
Solution: Assuming x1 = -1, y1 = 3, x2 = 2, y2 = 5, we obtain 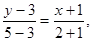 or
or 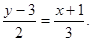
Thus, the required equation has the following form: 2x – 3y + 11 = 0. It is useful to check correctness of composing the equation. It is sufficiently to show that the coordinates of M and N satisfy the equation of the line. Indeed, the identities 2×(-1) - 3×3 + 11 = 0, 2×2 - 3×5 + 11 = 0 hold.
Rectangular coordinates in space. If a rectangular Cartesian system of coordinates is given in the space then a point M of space having the coordinates x (abscissa), y (ordinate) and z (z-coordinate) is denoted by M(x; y; z).
The distance between two points A(x1; y1; z1) and B(x2; y2; z2) is determined by the formula: 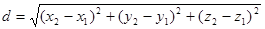 .
.
In particular, the distance from the origin of coordinates O to a point M(x; y; z) is determined as: 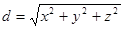 .
.
If a segment of which endpoints are A(x1; y1; z1) and B(x2; y2; z2) is divided by C(x; y; z) in ratio l then the coordinates of C are determined by the following formulas: 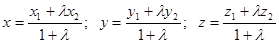
In particular, the coordinates of middle of a segment are determined as:
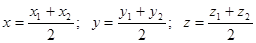
Common equation of a plane in the space. Let a plane Q pass through the point M0(x0, y0, z0) perpendicularly to the vector 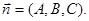 These conditions determine a unique plane in the space Oxyz. The vector
These conditions determine a unique plane in the space Oxyz. The vector 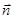 is the normal vector of the plane Q. Take an arbitrary point M(x, y, z) of the plane Q. Then the vector
is the normal vector of the plane Q. Take an arbitrary point M(x, y, z) of the plane Q. Then the vector 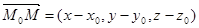 will be perpendicular to the vector
will be perpendicular to the vector 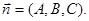 Hence, the scalar product of these vectors is equal to zero, i.e.
Hence, the scalar product of these vectors is equal to zero, i.e. 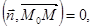 or
or 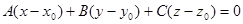
The last equation represents the equation of the plane which is perpendicular to the vector 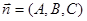 and passing through the point M0(x0, y0, z0).
and passing through the point M0(x0, y0, z0).
An equation of a plane which has been written down as 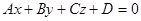 isa common equation of a plane. It can be proved that every equation of the first degree with three variables is an equation of a plane.
isa common equation of a plane. It can be proved that every equation of the first degree with three variables is an equation of a plane.
If D = 0, the equation 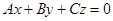 determines a plane passing through the origin of coordinates. Other special cases are determined by a position of the normal vector
determines a plane passing through the origin of coordinates. Other special cases are determined by a position of the normal vector 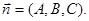 So, for example, if A = 0, the equation
So, for example, if A = 0, the equation 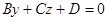 determines a plane which is parallel to the axis Ox; if A = D = 0, the equation
determines a plane which is parallel to the axis Ox; if A = D = 0, the equation 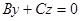 determines a plane passing through the axis Ox; if A = B = 0, the equation
determines a plane passing through the axis Ox; if A = B = 0, the equation 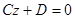 determines a plane which is parallel to the plane Oxy; if A = B = D = 0, the equation
determines a plane which is parallel to the plane Oxy; if A = B = D = 0, the equation 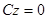 (or z = 0) determines the coordinate plane Oxy.
(or z = 0) determines the coordinate plane Oxy.
Conditions of parallelism and perpendicularity of planes are determined by conditions collinearity and perpendicularity of the normal vectors 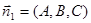 and
and 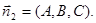
The condition of parallelism of two planes: 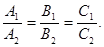
The condition of perpendicularity of two planes: 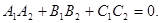
A line in the space can be set as the line of intersecting two planes, i.e. the set of points satisfying the system: 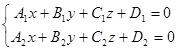
If the line is parallel to the vector  (the directing vector) and passes through the point M1 (x1, y1, z1), its equations can be obtained from the condition of collinearity of the vectors
(the directing vector) and passes through the point M1 (x1, y1, z1), its equations can be obtained from the condition of collinearity of the vectors 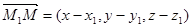 (where M (x, y, z) is an arbitrary point of the line) and
(where M (x, y, z) is an arbitrary point of the line) and 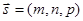 :
:
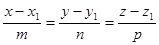
These equations are the canonical equations of a line in the space.
Glossary
segment– отрезок; axis (plural – axes) – ось
ratio – отношение, пропорция; polar – полярный
Cartesian system of coordinates – декартова система координат
the origin of coordinates – начало координат
common equation of a line – общее уравнение прямой
slope – угловой коэффициент
Exercises for Seminar 4
4.1. Find the distance between the points A(2; 3) and B(-10; -2).
4.2. Let A(-2; -5), B(4; 17) be given. The point C Î [AB] such that |AC| = 2|CB|. Find the coordinates of C.
4.3. Find the polar coordinates of the following points:
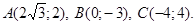
4.4. Find the rectangular coordinates of the points:
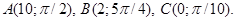
4.5. Compose the equation of a line cutting on the axis of ordinates the segment b = -3 and forming the angle a = p/6 with the positive direction of the axis of abscissas.
4.6. The equation of a line is given in the form: 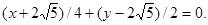
Write: a) common equation; b) equation with slope; c) equation in segments; d) normal equation.
4.7. Compose the equation of a line cutting on the axes of coordinates the segments a = 2/5 and b = – 1/10.
4.8. Show that the lines 4x – 6y + 7 = 0 and 20x – 30y – 11 = 0 are parallel.
4.9. Compose the equation of a line passing through the points A(-2; 4) and B(-2; -1).
4.10. Compose the equation of a line passing through the point M(-2; -5) and which is parallel to the line 3x + 4y + 2 = 0.
4.11. Determine the acute angle between the lines 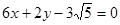 and
and 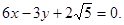
Exercises for Homework 4
4.12. Find the distance between the points 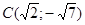 and
and 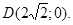
4.13. A point C(2; 3) is the middle of the segment AB. Find the coordinates of A if B(7; 5).
4.14. Find the polar coordinates of the points: 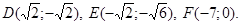
4.15. Find the rectangular coordinates of the points:
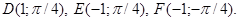
4.16. Compose the equation of a line cutting on the axis of ordinates the segment b = 1 and forming the angle a = 2p/3 with the positive direction of the axis of abscissas.
4.17. The equation of a line is given in the form: 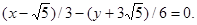
Write: a) common equation; b) equation with slope; c) equation in segments; d) normal equation.
4.18. Find the angle which is formed by the line 2x + 2y – 5 = 0 with the positive direction of the axis of abscissas.
4.19. Show that the lines 3x –5y + 7 = 0 and 10x + 6y – 3 = 0 are perpendicular.
4.20. Compose the equation of a line passing through the points A(-3; 4) and B(5; -6).
4.21. Compose the equation of a line passing through the point M(-3; 2) and which is perpendicular to the line 2x + y – 3 = 0.
