Методика расчета угла сдвига по граничным условиям
Рассмотрим явления, происходящие на огибающей LMB линий скольжения, ограничивающей зону разрушения грунта, в случае дальнейшего надвигания ножа на грунт (рисунок 2.1, а). Прежде всего, отметим, что непосредственно в момент разрушения грунта, при предельном равновесии, на площадках скольжения, появляющихся в зонах разрушения, выполняется условие (1.2). Это условие справедливо /78/ и для огибающей LMB линий скольжения. А это значит, что угол отклонения приведенных давлений, действующих на участках огибающей, будет равен углу внутреннего трения, т.е. dLMB= r.
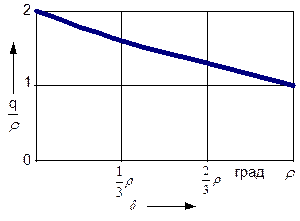
Выясним подробнее вопрос о влиянии угла отклонения приведенных давлений, действующих на откос, на устойчивость этого откоса. Проанализируем уравнения (1.19)...(1.21) для определения пассивного давления грунта на подпорную стенку. Анализ уравнений показывает, что наиболее опасным, с точки зрения устойчивости откоса, является действие на него со стороны подпорной стенки приведенных давлений, имеющих угол отклонения d=r. Это видно из рисунка 2.3, где представлены результаты расчетов для частного случая в относительных единицах. Для всех трех расчетных схем разрушающее давление будет минимальным при его отклонении на угол r.
 |  |
| а) | б) |
 | |
| в) | |
| Рисунок 2.3 Влияние угла отклонения на величину предельного давления: а) для решений с сингулярной точкой; б) для решений с линией разрыва; в) при непрерывном распределении напряжений. |
При приближении значений угла d отклонение приведенного давления q, действующего на откос, к величине угла внутреннего трения p линии скольжения приближаются к откосу ОВ, а зона A0OA1 стягиваются в точку 0.
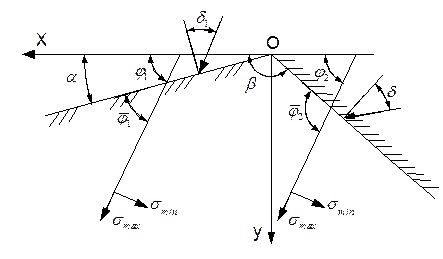 |
| Рисунок 2.5 Положительное направление углов. |
При выполнении условия d=r размеры всей области предельного состояния А0ОВ будут минимальны, а угол при вершине откоса b и угол сдвига y будут связаны зависимостью y=p-b.
Поскольку условие d=r на площадках скольжения выполняется только при предельном равновесии, то и устойчивость откоса будет критической непосредственно в момент сдвига грунта по огибающей LMB (рисунок 2.1, а).
Рассмотрим методику определения угла сдвига y при резании грунта, когда призма волочения отсутствует.
Приведенные на рисунке 2.5 положительные значения некоторых углов, а так же система координат приняты в соответствии с обозначениями В.В. Соколовского.
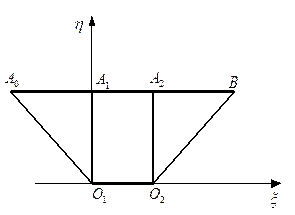 | |
| а) | |
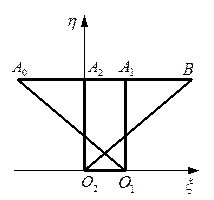 | 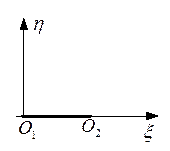 |
| б) | )в |
Рисунок 2.6 Характеристики в плоскости 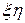 : а) при : а) при 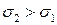 ; б) при ; б) при 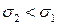 ; в) вырожденная трапеция. ; в) вырожденная трапеция. |
В общем случае характеристики в плоскости ζη будут иметь вид трапеции, представленной в развернутом виде на рисунке 2.6,а. Значение σ=σ2 в точке О2, принадлежащей зоне A2OB, должно быть больше, чем значение σ=σ1 в точке О1, принадлежащей зоне А0ОА1 (рисунок 2.6). В противном случае прямоугольные треугольники А0О1А1 и A2O2B будут иметь общие части, что показано на рисунке 2.6,б. Отметим, что при равномерном распределении давления вдоль поверхности засыпки и откоса для невесомой сыпучей среды зоны А0О1А1 и A2O2B трапеции
стягиваются в точку, а область А1A2O2О1 стягивается в прямую. Трапеция становится вырожденной и состоит из прямой О1О2 (рисунок 2.6,в).
