Определитель и обратная матрица

Они легко вычисляются методом исключения. В самом деле, вычитание строки из строки не изменяет значение определителя. Значит, в процессе исключения элементов (3.3), (3.4) абсолютная величина определителя не изменяется, а знак может измениться из-за перестановки строк. Определитель же треугольной матрицы (3.5) равен произведению диагональных элементов. Поэтому он вычисляется по формуле

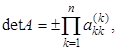(3.8)

где знак зависит от того, чётной или нечётной была суммарная перестановка строк.

Перейдём к вычислению обратной матрицы. Обозначим её элементы через a_im. Тогда соотношение AA ^{– 1} = E можно записать так:

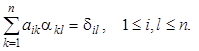(3.9)

Видно, что если рассматривать l-тый столбец обратной матрицы как вектор, то он является решением линейной системы (3.9) с матрицей А и специальной правой частью (в которой на l-том месте стоит единица, а на остальных – нули).

Таким образом, для обращения матрицы необходимо решить n систем линейных уравнений с n неизвестными с одинаковой матрицей А и разными правыми частями. Приведение матрицы А к треугольному виду по формулам (3.4), (3.5) выполняется при этом только один раз. В дальнейшем при помощи чисел c_mk по формуле (3.4) преобразуются все правые части, и для каждой правой части делается обратный ход.

Задание № 5

В ниже приведённых задачах требуется оценить обусловленность матрицы системы линейных алгебраических уравнений, решить систему, вычислить определитель матрицы и обратную матрицу.

Для сокращения записи в задачах приводится только матрица коэффициентов А и столбец свободных членов b, записанный иногда в строчку. В задачах, содержащих параметр, матрица коэффициентов получается в результате сложения матриц D и kC, где k – параметр, изменяющийся по некоторому закону.

Вариант А

1.

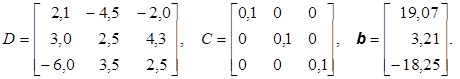
Вариант
k

2.

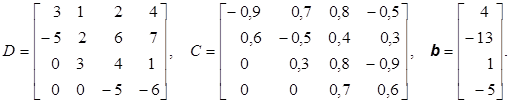
Вариант
k

3.

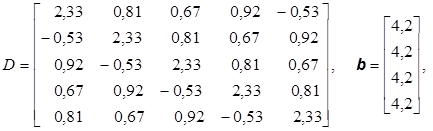
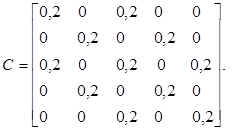
Вариант
k

4.

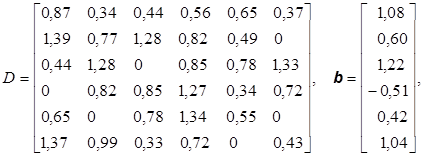
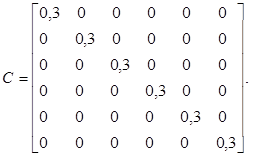
Вариант
k	0,5	1,0	1,5	2,0	2,5	3,0

Вариант Б

1.

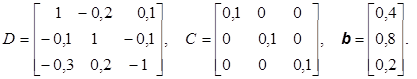
Вариант
k

2.

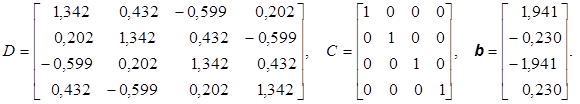
Вариант
k	0,02	0,04	0,06	0,08	0,10	0,12

3.

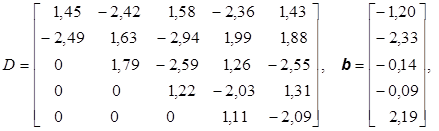
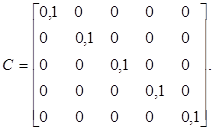
Вариант
k

4.

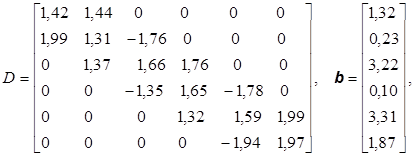
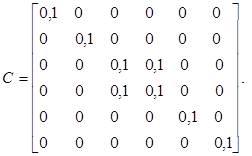
Вариант
k	1,5	3,5	5,5	7,5	9,5	11,5

Системы нелинейных уравнений

В общем случае, методы решения систем нелинейных уравнений можно рассматривать как своеобразное обобщение методов решения одного нелинейного уравнения. Эти методы подробно излагаются в литературе по численным методам и здесь не рассматриваются.

Метод простых итераций

Систему нелинейных уравнений можно кратко записать в векторном виде

f(x) =0, (3.10)

или более подробно в координатном представлении

f_k(x₁, x₂, ¼ , x_n) = 0, 1£ k £ n. (3.11)

Такие системы решают практически только итерационными методами. Нулевое приближение в случае двух переменных можно найти графически: построить на плоскости (х₁, х₂) кривые f₁(x₁, x₂) =0 и f₂(x₁, x₂) = 0 и найти точки их пересечения. Для трёх или более переменных (а также для комплексных корней) удовлетворительных способов подбора нулевых приближений нет.

В методе простых итераций, называемом также методом последовательных приближений, нелинейная система (3.11) заменяется эквивалентной системой х = j(х). Выбирается некоторое нулевое приближение х⁽⁰⁾ и дальнейшие приближения отыскиваются по формуле

x⁽ⁿ⁺¹⁾ = j(x⁽ⁿ⁾) (3.12)

или

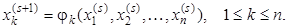(3,12,a)

Описанный выше в самой общей форме метод в литературе часто называют методом одновременных смещений или методом Якоби. Его сходимость можно улучшить, используя метод последовательных смещений или метод Гаусса – Зейделя. Отличие этого метода от предыдущего состоит в том, что только что найденные новые приближения в (k – 1)-ой точке (и всех предыдущих) используются для отыскания нового приближения в последующих точках (или для последующих переменных). Основным уравнением метода последовательных смещений является выражение

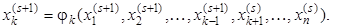(3.13)

Метод Ньютона

Пусть известно некоторое приближение х^(s) к корню 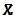Запишем исходную систему (3.10) в виде f(x^(s) + D x) = 0, где D х = 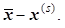Разлагая эти уравнения в ряды и ограничиваясь первыми дифференциалами, т.е. линеаризуя функцию, получим

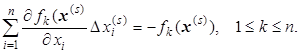(3.14)

Эта система уравнений линейна относительно приращений 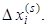Все коэффициенты этой системы выражаются через последнее приближение x^(s). Решив эту систему (например, методом исключения), найдём новое приближение x^(s+1) = x^(s) + D x^(s).

Методы спуска

Рассмотрим функцию F(x) = 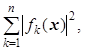образованную из исходной системы уравнений. Она неотрицательна и обращается в нуль в том и только в том случае, когда f(x) = 0. Таким образом, решение исходной системы уравнений (5.10) будет одновременно и минимумом скалярной функции многих переменных Ф(х).

Замечание 1. – В принципе, все вышеописанные методы решения систем нелинейных уравнений неявно "задействованы" в командах и функциях распространённых ныне математических пакетов. Правда, ни в документации этих пакетов, ни в литературе не указывается, для какого порядка систем "работоспособны" эти функции. Поскольку при их использовании необходимо задавать нулевые приближения, то, по-видимому, число уравнений системы не должно быть слишком велико.

Замечание 2. – Для систем уравнений невысокого порядка удобны пакеты Mathcad, Mapleи Mathematica. Рассмотрим использование первого из них на следующем примере.

Пусть требуется решить следующую систему уравнений

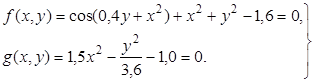
Начальные приближения найдём графически. Для этого в соответствии с правилами Mathcadсформируем матрицы значений функций, образующих уравнения системы, и построим соответствующие контурные графики:

f(x, y) : = cos(0.4×y + x²) + x² + y² – 1.6 g(x, y) : = 1.5×x² -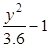

i:= 0..100 j:= 0..100 x_i := 0.02×i y_j := - 1 + 0.02×j F_{i, j} := f(x_i, y_j)

G_{i, j} := g(x_i, y_j)

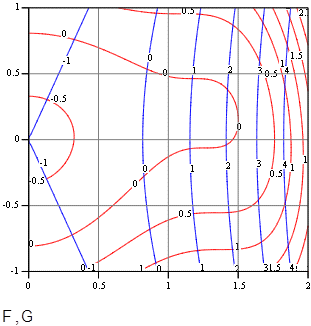
Как видно из сопоставления контурных линий, приведённых на последующем рисунке и соответствующих нулевому значению функций, эти линии пересекаются в двух точках: (х » 1, у » 0,45) и (х » 0,8, у » - 0,3). Используя эти приближения, воспользуемся совокупностью команд Given и Find:

x : = 1.0 y : = 0.45

Given

cos(0.4×y + x²) + x² + y² =1.6

1.5×x² -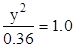

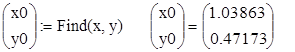
Для второго решения аналогично имеем

x : = 0.8 y : = - 0.25

Given

cos(0.4×y + x²) + x² + y² =1.6

1.5×x² -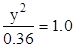

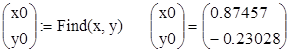
В рамках Mapleсистема нелинейных уравнений решается при помощи команды fsolve({eqn1, eqn2, …}, {v1, v2, …}, options), где аргумент optionsиспользуется для указания примерных интервалов расположения корней. По сравнению с Mathcadданный пакет имеет то преимущество, что позволяет совмещать контурные графики и, тем самым, более точно устанавливать нулевые приближённые решения.

Для данного примера использование пакета Mapleбудет выглядеть так:

> restart; with(plots):

> v1 := contourplot(cos(0.4*y+x^2)+x^2+y^2-1.6, x=0..2,y= - 1.0..1.0, grid = [15, 15],

contours = [-0.5, 0, 0.5], numpoints = 1600, colour = blue):

> v2 := contourplot(1.5*x^2-y^2/0.36-1., x=0..2, y= - 1.0..1.0, grid = [15, 15],

contours = [-0.5, 0, 0.5], numpoints = 1600, colour = red):

> plots[display]([v1, v2]);

Результат этих действий показан на вышеприведённом рисунке. Конечно, здесь также имеется вполне определённый недостаток, связанный с тем, что графика Maple"не признаёт" координатной сетки. Тем не менее, рисунок очень нагляден, особенно если учесть, что значения контурных линий возрастает слева направо.

Дальнейшая процедура использования пакета вполне определена:

> fsolve({cos(0.4*y+x^2)+x^2+y^2-1.6=0, 1.5*x^2-y^2/0.36-1.=0}, {x, y},

x=1.0 . . 1.2, y=0.4 . . 0.5);

{x = 1.038629238, y = .4717259527}

> fsolve({cos(0.4*y+x^2)+x^2+y^2-1.6=0, 1.5*x^2-y^2/0.36-1.=0}, {x, y},

x=0.8 . . 1.2);

{x = .8745654831, y = - .2302758856}

Пример3.1. Решить систему уравнений

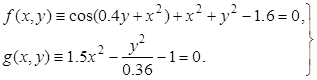
Начальное приближение найти графически.

Из первого уравнения следует, что 0.6 £ x² + y² £ 2.6. Поэтому график g(x, y) достаточно построить для значений x Î [0.82, 1.4]. Кривую g(x, y) на этом промежутке построим по следующим точкам:

x	0.82	1.0	1.1	1.2	1.3	1.4
y	0.0	0.42	0.54	0.65	0.74	0.83

Введём обозначение

0.4y + x² = q. (a)

Тогда из первого уравнения следует

cos(q) + x² + y² –1.6 = 0. (b)

Как видно из таблицы, нас интересуют значения q лишь в промежутке 0.6 < q < 2.3. Разрешим равенства (а) и (b) относительно x и y:

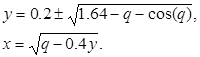
Придавая q различные значения, получим ряд точек на кривой f(x, y) = 0:

q	1.0	1.1	1.2	1.3
x	0.89	0.94	1.00	1.05
y	0.52	0.50	0.48	0.47

По данным таблиц строим график:

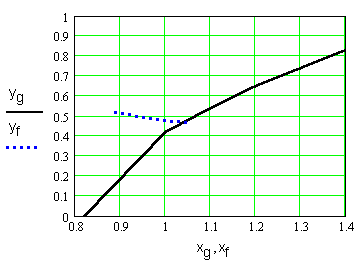Из графика видно, что начальное приближение составляет: x₀ = 1.04, y₀ = 0.47. Полученное приближенное решение уточним по методу Ньютона

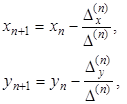
где

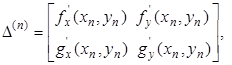
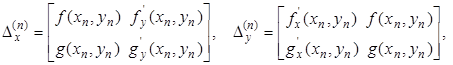
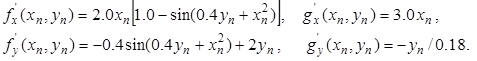
Все вычисления вносим в две таблицы, где dx и dy обозначают соответственно 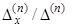и .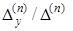

Основная таблица	Вспомогательная таблица
x	1.04	1.03864	x	1.04	1.03864
y	0.47	0.47173	y	0.47	0.47173
f	- 0.00084	0.00000	0.4y	0.188	0.18869
g	0.00879	0.00002	x2	1.0816	1.07877
fx'	0.09364	0.09483	a = 0.4y + x2	1.2696	1.26746
fy'	0.55801	0.56172	cos(a)	0.29666	0.29870
gx'	3.12	3.11592	1.5 x2	1.6224	1.61816
gy'	- 2.61111	- 2.62072	y2	0.2209	0.22253
Dx	0.00271	0.00001	y2/0.36	0.61361	0.61814
Dy	- 0.00344	0.00000	2 x	2.08	2.07728
D	- 1.98549	- 1.99889	-2 x×sin(a)	- 1.98636	- 1.98245
dx	0.00136	0.00000	- 0.4×sin(a)	- 0.38119	- 0.38174
dy	- 0.00173	0.00000

Ответ: x = 1.03864; y = 0.47173.

Этот ответ полностью совпадает с приведённым выше первым решением, однако второе решение при таком подходе не выявляется. Необходимо строить полный график функций, а не его отдельные линии.

Задание № 6

Разработать алгоритм решения методом Ньютона системы двух нелинейных уравнений, составить программу реализации алгоритма (допускается любой язык программирования) и получить решения с точностью до пяти знаков после запятой. Начальные приближения найти графически.

Проверить точность решения, используя любой из вышеупомянутых пакетов.

Вариант А

Вариант	Система уравнений	а	k
	sin(x + ky) – x + y2 = 0 (y +0.1)2 + x2 = a	0,6	- 0,5
	- " -	0,7	- 0,4
	- " -	0,8	- 0,3
	- " -	0,9	- 0,2
	- " -	1,0	- 0,1
	- " -	1,1	0,0
	tg(x – y + k) – xy = 0 ax2 +2y2 = 1	0,5	0,2
	- " -	0,6	0,1
	- " -	0,7	0,0
	- " -	0,8	- 0,1
	- " -	0,9	- 0,2
	- " -	1,0	- 0,3
	cos(x2 + y2) – x + y = a	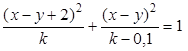0,0	0,4
	- " -	0,1	0,6
	- " -	0,2	0,8
	- " -	0,3	1,0
	- " -	0,4	1,2
	- " -	0,5	1,4
	ex + y – x2 + y = k (x +0,5)2 + y2 = a	1,0	2,0
	- " -	1,2	2,2
	- " -	1,4	2,4
	- " -	1,6	2,6
	- " -	1,8	2,8
	- " -	2,0	3,0

Вариант Б

Вариант	Система уравнений	а	k
	th(x2 – y) – k(x + y) = 0 (x – 0,2)2 – ay2 = 1,5		0,44
	- " -		0,46
	- " -		0,48
	- " -		0,50
	- " -		0,52
	- " -		0,54
	ekx + y – xy = 1,4	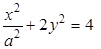0,7	- 0,10
	- " -	0,8	- 0,15
	- " -	0,9	- 0,20
	- " -	1,0	- 0,25
	- " -	1,1	- 0,30
	- " -	1,2	-0,35
	tg(ax + y) – axy = 0,3 x2 + y2 = k	- 1,2	1,3
	- " -	- 1,0	1,5
	- " -	- 0,8	1,7
	- " -	- 0,6	1,9
	- " -	- 0,4	2,1
	- " -	- 0,2	2,3
	cos(ky + x2) + x2 + y2 = 1,6 1,5(x + 0,1) -	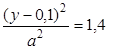0,6	0,6
	- " -	0,8	0,7
	- " -	1,0	0,8
	- " -	1,2	0,9
	- " -	1,4	1,0
	- " -	1,6	1,1