Рассмотренная теорема является следствием следующей теоремы.
Теорема. Компоненты оптимального решения двойственной задачи равны абсолютным значениям коэффициентов при соответствующих переменных целевой функции исходной задачи, выраженной через свободные переменные ее оптимального решения.
Пример 1. Даны две взаимно двойственные задачи:
L=2x1+3x2®max при ограничениях 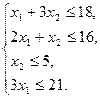 x1³0, x2³ | Z=18y1+16y2+5y3+21y4®min при ограничениях:  |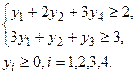
Эти задачи решены ранее и получены оптимумы линейных функций Lmax=24, Zmin=24. Убедимся в справедливости второй теоремы двойственности.
Установим следующее соответствие между переменными:
| x1 x2 x3 x4 x5 x6 ↕ ↕ ↕ ↕ ↕ ↕ y5 y6 y1 y2 y3 y4 |
Обе задачи были решены симплексным и на последнем шаге решения каждой задачи получено 7
| L=24-4/5x3-3/5x4-0x5-0x6-0x1-0x2 L(X*)=Lmax=24 при оптимальном базисном решении X*=(6;4;0;0;1;3) | Z=24+6y5+4y6+0y1+0y2+ y3+3y4 Z(Y*)=Zmin=24 при оптимальном базисном решении Y*=(4/5;3/5;0;0;0;0) |
Компоненты оптимального решения двойственной задачи (4/5;3/5;0;0;0;0) равны по абсолютной величине коэффициентам при соответствующих переменных целевой функции L, а компоненты оптимального решения исходной задачи (6;4;0;0;1;3) равны коэффициентам при соответствующих переменных целевой функции Z.
Вторая теорема двойственности . Для того чтобы допустимые решения Х*=( x*1, x*2 , …x*j, …, x*n), Y*=( y*1, y*2 , …, y*i, …, y*m) являлись оптимальными решениями пары двойственных задач, необходимо и достаточно, чтобы выполнялись следующие равенства:
a) 
b) 
Иначе, a) если при подстановке оптимального решения в систему ограничений j-е ограничение двойственной задачи выполняется как строгое неравенство, т.е., 
, то j-я компонента оптимального решения исходной задачи 
, и, наоборот, если j-я координата оптимального решения задачи 
, то j-е ограничение двойственной задачи 
;
б) если при подстановке оптимального решения в систему ограничений i-е ограничение исходной задачи 
, то i-я компонента оптимального решения двойственной задачи 
, и, наоборот, если i-я координата оптимального решения двойственной задачи 
, то i-е ограничение исходной задачи 
(без доказательства).
Пример. Для задачи составить двойственную, получить решение, например графически и, используя 2-ю теорему двойственности, найти решение исходной задачи:
L(X)=-2x1+4x2+14x3+2x4®min,
Решение. Составим двойственную задачу: Z(Y)+6y1+30y2®max,
Пусть получили оптимальное решение Y*=(2;3), значение Z(Y*)=102. Подставим оптимальное решение Y*=(2;3) в систему ограничений. Получим, что ограничения (1) и (4) выполняются как строгие неравенства: 
Согласно 2-й теореме двойственности соответствующие координаты исходной задачи, равны 0: x*1=x*4=0. Учитывая это, из системы ограничений исходной задачи получим 
Отсюда х*3=7, х*2=1. Х*=(0,1,7,0); minL(X)=102.