Этапы технологического цикла вычислительного эксперимента

В настоящее время основным способом исследования математической модели и проверки ее качественных показателей служит вычислительный эксперимент

Вычислительным экспериментом называется методология и технология исследований, основанные на применении прикладной математики и ЭВМ как технической базы при использовании математических моделей.

Таким образом, математические структуры вместе с описанием соответствия экспериментально обнаруженным свойствам объекта и являются моделью изучаемого объекта, отражая в математической, символической (знаковой) форме объективно существующие в природе зависимости, связи и законы.

На основе математического моделирования и методов вычислительной математики создались теория и практика вычислительного эксперимента, технологический цикл которого принято разделять на следующие этапы .

1. Для исследуемого объекта строится модель, обычно сначала физическая, фиксирующая разделение всех действующих в явлении (процессе) факторов на главные и второстепенные, которые на данном этапе исследования отбрасываются; одновременно формулируются допущения и условия применимости модели, границы, в которых будут справедливы полученные результаты .

2. Разрабатывается метод решения сформулированной математической задачи. Эта задача представляется в виде совокупности алгебраических формул, по которым должны вестись вычисления и условия, показывающие последовательность применения этих формул; в результате такого эксперимента часто ставится задача определения оптимального набора параметров.

3. Разрабатываются алгоритм и программа решения задачи на ЭВМ. Программирование решений определяется теперь не только искусством и опытом исполнителя, а перерастает в самостоятельную науку со своими принципиальными подходами.

4. Проведение расчетов на ЭВМ. Результат получается в виде некоторой цифровой информации, которую далее необходимо будет расшифровать. Точность полученной информации определяется при вычислительном эксперименте достоверностью модели, положенной в основу эксперимента, правильностью алгоритмов и программ (проводятся предварительные «тестовые» испытания).

5. Обработка результатов расчетов, их анализ и выводы . На этом этапе могут возникнуть необходимость уточнения математической модели (усложнения или, наоборот, упрощения), предложения по созданию упрощенных инженерных способов решения и формул.

Вычислительный эксперимент приобретает исключительное значение в тех случаях, когда натурные эксперименты и построение физической модели оказываются невозможными.

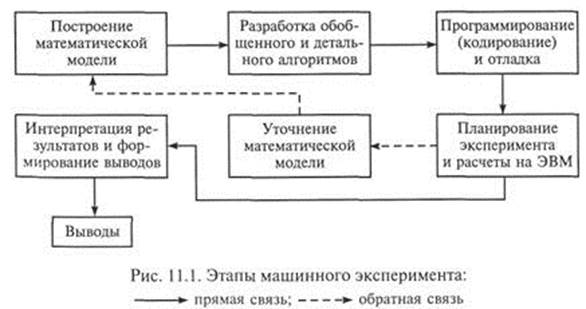
Каждому из показанных на рисунке этапов присущи собственные приемы, методы, технологии. Все эти этапы носят ярко выраженный творческий характер и требуют от разработчика модели особой подготовки.

Планирование эксперимента

При современном уравне развития науки и техники многие исследования требуют постановки сложных и дорогостоящих экспериментов. До последнего времени выбор самого эксперимента, где , как и когда его проводить определялся в основном интуицией экпериментатора. Однако с учетом возросшей стоимости проведения эксперимента актуальной становится проблема извлечения наибольшего количества информации с наименьшими затратами. В этой связи становится необходимым применение методов, которые давали бы не только способ обработки экспериментальных данных, но позволяли бы оптимальным образом организовывать эксперимент. Математический аппарат оптимального планирования эксперимента базируется на применении методов математической статистики и методов решения экстремальных задач. Методы математической статистики используются для обоснования разумного выбора критерия оптимальности, после чего проблема оптимальной задачи планирования эксперимента решается как некоторая экстремальная задача.

К настоящему времени можно выделить два основных направления в планировании экспериментов: планирование экстремальных экспериментов и планирование экспериментов по выявлению сути явлений.

В рамках первого направления исследуются условия, при которых процесс удовлетворяет некоторому критерию оптимальности. В рамках второго направления исследуется взаимосвязь между различными параметрами т.е фактически решается задача идентификации модели объекта при различной априорной информации. Предоставив в результате исследований некоторую математическую зависимость между параметрами, мы даем исследователю возможность обобщить полученные результаты в части выявления взаимосвязи явлений.

Рассмотрим подробнее математическую постановку проблемы планирования эксперимента по выявлению механизма явления. Обычно измеряемая величина зависит от ряда параметров , которые будем называть контролируемыми величинами, которые можно представить в виде вектора столбца

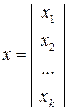
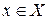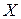, где -факторное пространство.

Определение области возможных значений контролируемых величин играет важную роль при планировании экспериментов. Задачей эксперимента по поиску математической модели является отыскание связи между измеряемыми величинами и контролируемыми переменными. Эту свазь можно записать в виде

,

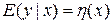где 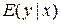-условное математическое ожидание при значении контролируемых переменных. Можно рассмотреть три постановки задачи в зависимости от априорной информации

1. Вид функции 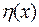известен. Требуется определить или уточнить неизвестные параметры

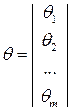
2. Известно, что 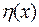совпадает с одной из функций

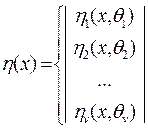
Требуется определить, какая из функций 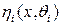является истиной и найти неизвестные параметры.

3. Вид функции 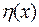неизвестен. Известно лишь, что в интересующей области она может быть достаточно хорошо аппроксимирована конечным рядом по некоторой системе наперед заданных функций Требуется найти наилучшее описание функции .

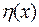Оптимизация в исследовании - (от лат. optimus-наилучший) Под оптимизацией- понимают целенаправленную деятельность, заключающуюся в получении наилучших результатов при соответствующих условиях. Постановка задачи оптимизации предполагает наличие объекта, набора независимых параметров (переменных), описывающих данную задачу, а также условий (часто наз. ограничениями), характеризующих приемлемые значения независимых переменных, которые и образуют модель рассматриваемой системы. Еще одним обязательным условием описания оптимизационной задачи служит мера "качества", носящая название критерия оптимизации и зависящая от переменных . Оптимальное решение оптимизационной задачи - поиск определенного набора значений переменных, которому отвечает минимальное значение критерия оптимальности.

Описанные и построенные модели реального объекта – важнейший этап оптимизационного исследования, так как он определяет практическую ценность получаемого решения и возможность его реализации.

Процесс оптимизации с использованием модели можно рассматривать как метод отыскания оптимального решения для реального объекта без непосредственного экспериментирования с самим объектом. «Прямой» путь, ведущий к оптимальному решению, заменяется «обходным», включающим построение и оптимизацию модели, а также преобразование полученных результатов в практически реализуемую форму. При формировании такой модели следует учитывать характеристики объекта, которые должны быть отражены в модели, а менее существенные особенности в модель можно не включать. Необходимо сформулировать логически обоснованные допущения, выбрать форму представления модели, уровень ее детализации и метод реализации на ЭВМ. Все это относятся к этапу построения модели. Модели можно упорядочить по степени адекватности описания поведения реального объекта. Таким образом, качество модели нельзя оценивать ни по структуре, ни по форме. Единственным критерием такой оценки может служить лишь достоверность полученных на модели примеров поведения реального объекта.