Аналогично как в предыдущих

Ответ: -3

44. Дайте определение числового ряда и его суммы. Найдите, исходя из определения, сумму ряда при 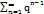при

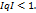
Определение.Пусть дана числовая последовательность а₁ ,а₂, а₃….a_n . Выражение вида

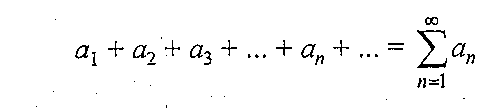
называют числовым рядом,или просто рядом.

Числа а₁ ,а₂, а₃,….a_n называют членами ряда, число а_п с общим номером п называют общим членом ряда.

Суммы конечного числа первых членов ряда

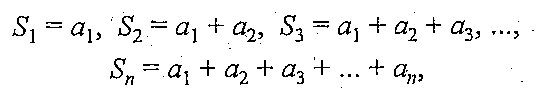
называют частичными суммами ряда. Так как число членов ряда бесконечно, то частичные суммы образуют числовую последовательность

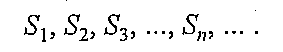
45. Дайте определения числового ряда и его суммы. Исходя из определения докажите, что сумма 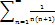ряда равна числу 1.

Так как 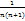= - 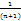, то для n-ной частичной суммы ряда получим выражение :
Sn=(1- )+( - ).
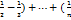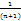Sn= 1- 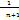.Cледовательно, 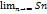=1.Итак, ряд схотится и сумма его равна 1.

46. Сформулируйте и докажите необходимое условие сходимости числового ряда. Приведите пример расходящегося ряда, для которого это условие выполнено.

Если ряд сходится ,то предел его общего члена =0.
Док-во: Пусть данный ряд сходится и его сумма равна S. Для любого натурального n имеем 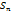= 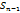+ 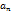, или = - .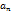
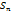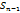При n 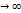обе частичные суммы 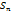и 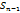стремятся к пределу S, поэтому из равенства следует,что
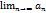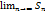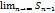= - =S-S=0 .

47. Докажите, что если ряд сходится 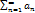, а ряд 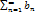расходится, то ряд

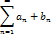
48. Докажите, что для сходимости ряда 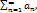, 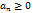необходимо и достаточно, чтобы последовательность его частичных сумм была ограничена.
Док-во: Пусть ряд 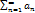сходится. Тогда существует предел его частичных сумм. Из свойств пределов следует,что посл-ть частичных сумм ограничена.
Достаточность: Т.к. все члены данного ряда положительны и для любого n Но известно, что ограниченная сверху монотонная последовательность имеет предел.

49. Сформулируйте и докажите признак Даламбера для числовых рядов с положительными членами.

Если для ряда с положительными членами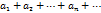

сущ. такое число q 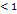, то при всех n выполняется неравенство:

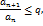то ряд сходится .Если же 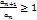для всех n, то ряд расходится.

Док-во:Отбросив несколько первых членов ряда,можно считать,что неравенство выполняется для всех n=1, 2… Перепишем это неравенство в виде .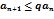
Jnc.lf bvttv 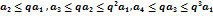и т.д.Вообще для любого n справедливо неравенство
.
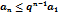Это показывает , что члены ряда 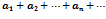не превосходят соответсвующих членов геометр прогрессии
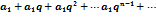Т.к. по условию 0 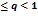, это прогрессия сходится.В силу первого признака сравнения сходится и данный ряд.
В случае,когда , то есть члены ряда образуют неубывающую последовательность, и поэтому не выполняется необходимый признак сходимости ряда , который полностью доказывает теорему.

50.Сформулируйте признак Даламбера в предельной форме. Приведите пример сходящегося ряда с положительными членами, к которому этот признак неприменим.

Если существует предел: 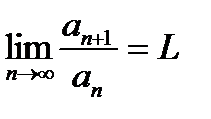, то

1) при L < 1 ряд сходится

2) при L > 1 ряд расходится

3) при L = 1 необходимы доп. исследования. (признак неприменим)

Пример:

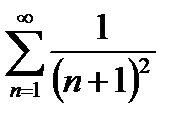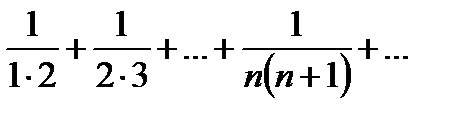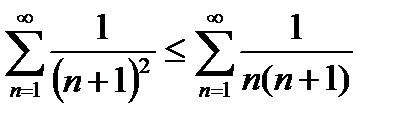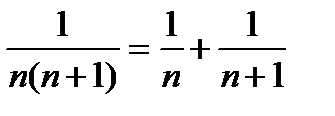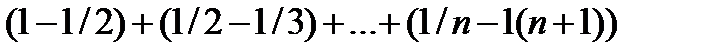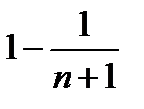Докажем сходимость: сравним с рядом: . Поскольку при всех n => достаточно доказать сходимость этого ряда. Так как , то = Т.о. 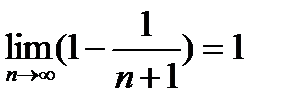. Этот ряд сходится => искомый ряд тоже сходится. Признак Даламбера не работает: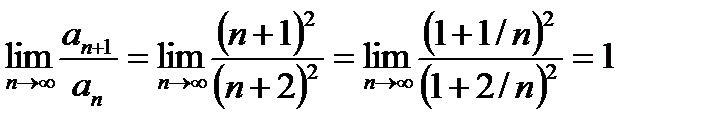

51. Сформулируйте признаки сравнения для числовых рядов с неотрицательными членами. Используя этот признак, докажите, что ряд 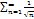расходится .

52. Сформулируйте интегральный признак сходимости числового ряда с положительными членами. При каких положительных значениях ряд сходится, а при каких расходится? Ответ обоснуйте.  1 1 n n

53.Дайте определение гармонического ряда. Докажите, что гармонический ряд расходится.

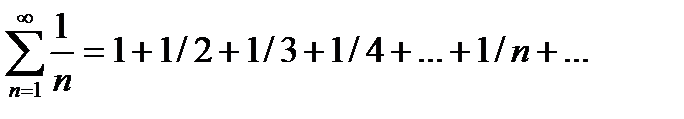- гармонический ряд.

Док-во расходимости:

По интегральному признаку Коши: f(x)= 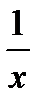- монотонно убывает на [1;∞), f(x)→0 при x→∞. Тогда 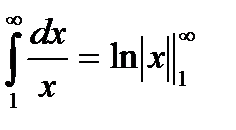= lim(lnx)-ln1 = ∞ => ряд расходится

54.Сформулируйте признак Лейбница для знакочередующихся числовых рядов. Приведите пример знакочередующегося ряда, сходящегося условно.

Если члены знакочередующегося ряда убывают по модулю ( 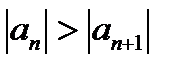) и стремятся к нулю, когда n®µ,то 1) ряд сходится; 2) любой остаток ряда не превосходит по абсолютной величине первого из своих членов и имеет одинаковый с ним знак.

Условная сходимость – это когда сам ряд сходится, а ряд, составленный их модулей членов – расходится. Пример:

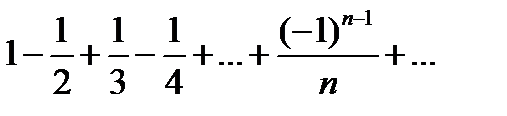- по Т.Лейбница сходится. Но ряд модулей расходится: 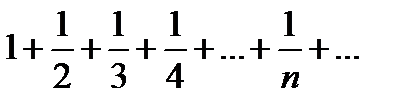(гармонический ряд).