РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА. Найти предел (не пользуясь правилом Лопиталя):
ЗАДАНИЕ 1
Найти предел (не пользуясь правилом Лопиталя):
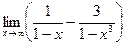 | 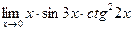 | ||
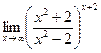 | 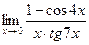 | ||
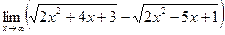 | 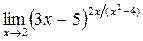 | ||
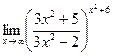 | 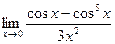 | ||
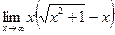 | 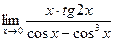 | ||
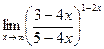 | 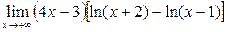 | ||
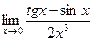 | 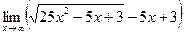 | ||
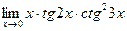 | 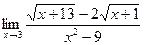 | ||
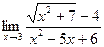 | 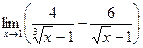 | ||
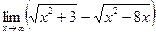 | 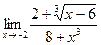 | ||
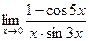 | 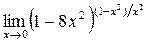 | ||
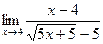 | 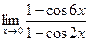 | ||
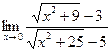 | 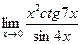 | ||
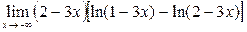 | 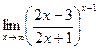 | ||
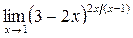 | 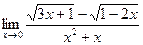 |
ЗАДАНИЕ 2
Построить функцию и исследовать характер точек разрыва
| 1. | 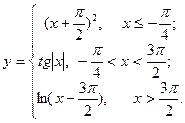 | 16. | 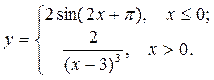 |
| 2. | 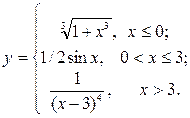 | 17. | 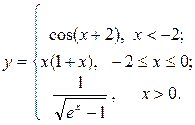 |
| 3. | 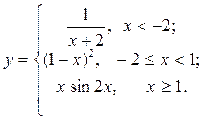 | 18. | 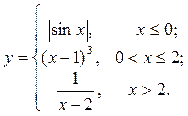 |
| 4. | 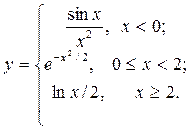 | 19. | 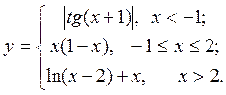 |
| 5. | 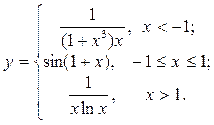 | 20. | 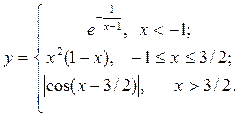 |
| 6. | 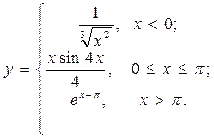 | 21. | 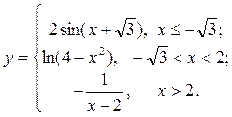 |
| 7. | 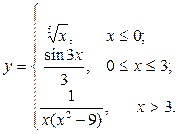 | 22. | 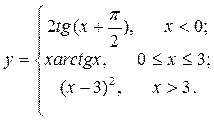 |
| 8. | 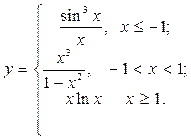 | 23. | 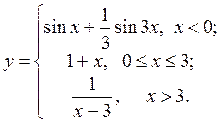 |
| 9. | 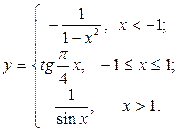 | 24. | 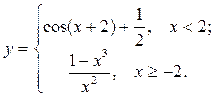 |
| 10. | 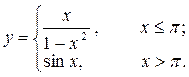 | 25. | 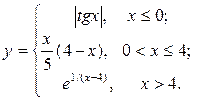 |
| 11. | 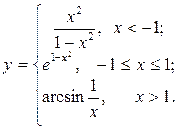 | 26. | 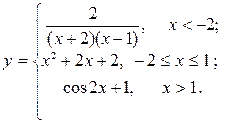 |
| 12. | 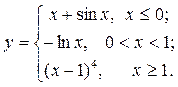 | 27. | 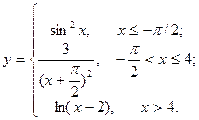 |
| 13. | 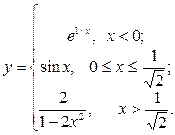 | 28. | 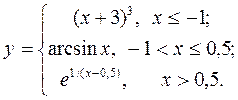 |
| 14. | 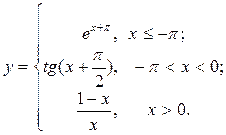 | 29. | 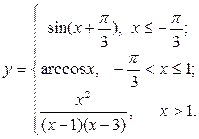 |
| 15. | 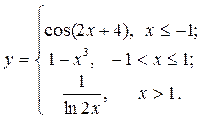 | 30. | 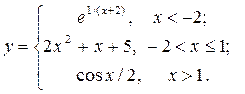 |
ЗАДАНИЕ 3
Подобрать a так, чтобы функция была непрерывной. Доказать непрерывность функции при найденном a и разрывность при каком-либо другом a1. Построить графики функций для обоих случаев.
| 1. | 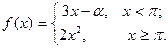 | 16. | 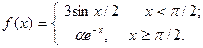 |
| 2. | 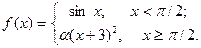 | 17. | 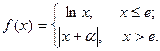 |
| 3. | 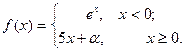 | 18. | 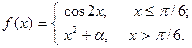 |
| 4. | 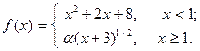 | 19. | 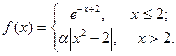 |
| 5. | 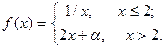 | 20. | 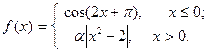 |
| 6. | 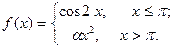 | 21. | 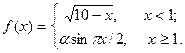 |
| 7. | 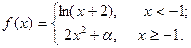 | 22. | 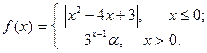 |
| 8. | 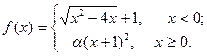 | 23. | 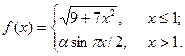 |
| 9. | 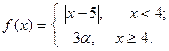 | 24. | 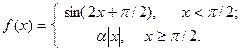 |
| 10. | 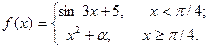 | 25. | 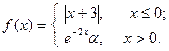 |
| 11. | 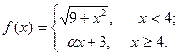 | 26. | 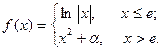 |
| 12. | 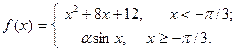 | 27. | 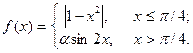 |
| 13. | 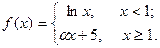 | 28. | 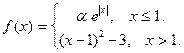 |
| 14. | 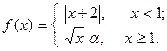 | 29. | 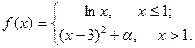 |
| 15. | 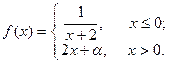 | 30. | 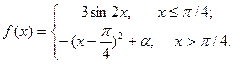 |
ЗАДАНИЕ 4
Исследовать функцию у = f(x) и схематично построить ее график.
| 1. | y = (2x2 –5x+4)ex | 11. | y = 1 – 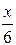 +arctg(x/3) +arctg(x/3) | 21. | y = (3lnx–1) x3 |
| 2. | y = (lnx-2) 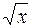 | 12. | y = 8x2+10x+ln½x½ | 22. | y= 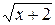 (3,8+1,3x– 0,3x2) (3,8+1,3x– 0,3x2) |
| 3. | у = 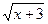 (3,3+0,2x–0,3x2) (3,3+0,2x–0,3x2) | 13. | y = xln(x2+0,36) –2x+1,2arctg 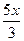 | 23. | y = 2ln(x2+1) –3arctgx |
| 4. | y = 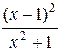 | 14. | y = (2x2+9x+11)e-x | 24. | y = 0,3x–1–arctg3x |
| 5. | y = 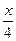 –1–arctg(x/2) –1–arctg(x/2) | 15. | y = (2lnx–1) x2 | 25. | y = (x2–5) 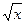 |
| 6. | y = 2x2+5x+ln½x½ | 16. | y = 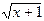 (1,7+1,4x–0,3x2) (1,7+1,4x–0,3x2) | 26. | y = 0,5ln(x2+9)– 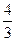 arctg arctg 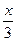 |
| 7. | y = (2x2+3x+2)e-x | 17. | y = 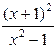 | 27. | y = x1/3 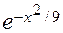 |
| 8. | y = x3/2(lnx– 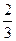 ) ) | 18. | y = 1– 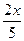 +arctg2x +arctg2x | 28. | y = 16x–arcsin2x |
| 9. | y = 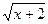 (2,8+0,8x–0,3x2) (2,8+0,8x–0,3x2) | 19. | y = ln(x2–x+1) | 29. | y = ln(x2–4x+13) |
| 10. | y = 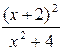 | 20. | y = (2x2+x+1)ex | 30. | y = 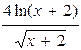 |
ЗАДАНИЕ 5
Найти неопределенные интегралы:
| Вар. | а) | б) | в) | г) |
| 1. | 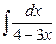 | 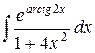 | 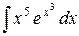 | 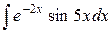 |
| 2. | 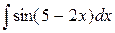 | 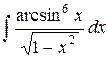 | 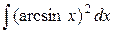 | 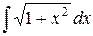 |
| 3. | 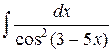 | 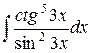 | 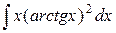 | 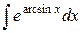 |
| 4. | 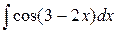 | 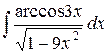 | 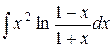 | 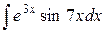 |
| 5. | 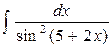 | 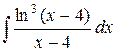 | 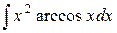 | 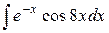 |
| 6. | 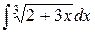 | 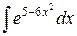 | 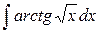 | 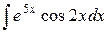 |
| 7. | 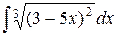 | 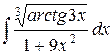 | 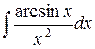 | 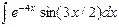 |
| 8. | 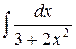 | 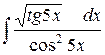 | 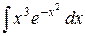 | 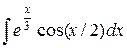 |
| 9. | 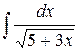 | 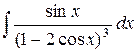 | 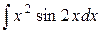 | 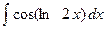 |
| 10. | 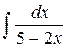 | 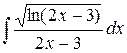 | 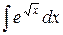 | 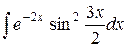 |
| 11. | 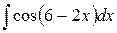 | 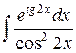 | 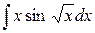 | 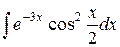 |
| 12. | 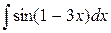 | 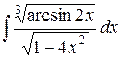 | 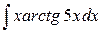 | 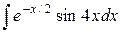 |
| 13. | 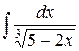 | 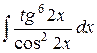 | 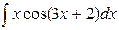 | 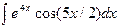 |
| 14. | 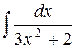 | 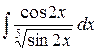 | 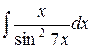 | 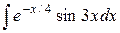 |
| 15. | 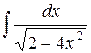 | 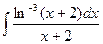 | 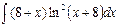 | 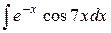 |
| 16. | 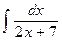 | 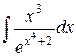 | 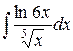 | 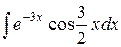 |
| 17. | 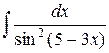 | 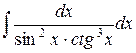 | 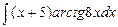 | 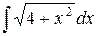 |
| 18. | 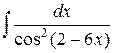 | 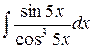 | 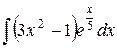 | 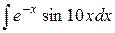 |
| 19. | 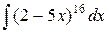 | 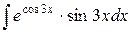 | 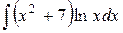 | 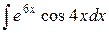 |
| 20. | 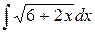 | 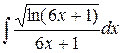 | 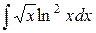 | 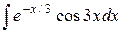 |
| 21. | 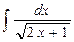 | 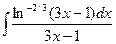 | 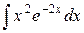 | 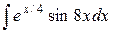 |
| 22. | 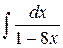 | 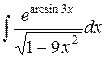 | 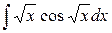 | 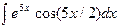 |
| 23. | 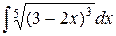 | 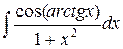 | 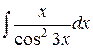 | 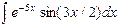 |
| 24. | 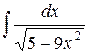 | 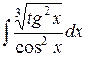 | 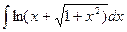 | 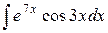 |
| 25. | 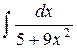 | 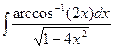 | 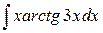 | 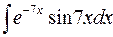 |
| 26. | 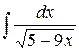 | 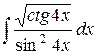 | 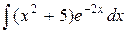 | 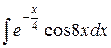 |
| 27. | 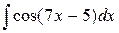 | 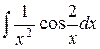 | 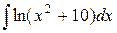 | 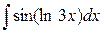 |
| 28. | 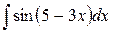 | 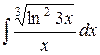 | 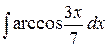 | 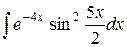 |
| 29. | 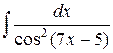 | 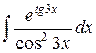 | 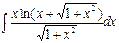 | 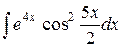 |
| 30. | 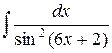 | 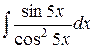 | 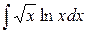 | 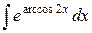 |
ЗАДАНИЕ 6
Вычислить неопределенные интегралы от рациональных алгебраических функций.
| 1. | 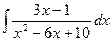 | 11. | 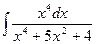 | 21. | 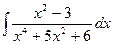 |
| 2. | 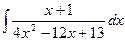 | 12. | 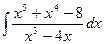 | 22. | 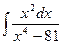 |
| 3. | 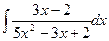 | 13. | 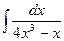 | 23. | 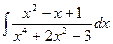 |
| 4. | 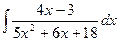 | 14. | 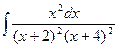 | 24. | 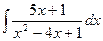 |
| 5. | 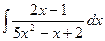 | 15. | 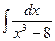 | 25. | 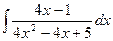 |
| 6. | 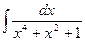 | 16. | 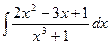 | 26. | 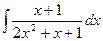 |
| 7. | 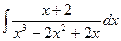 | 17. | 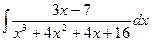 | 27. | 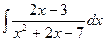 |
| 8. | 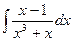 | 18. | 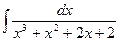 | 28. | 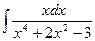 |
| 9. | 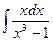 | 19. | 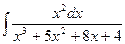 | 29. | 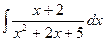 |
| 10. | 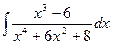 | 20. | 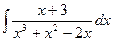 | 30. | 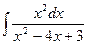 |
ЗАДАНИЕ 7
Вычислить неопределенные интегралы от иррациональных алгебраических функций.
| 1. | 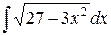 | 11. | 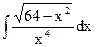 | 21. | 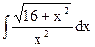 |
| 2. | 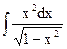 | 12. | 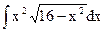 | 22. | 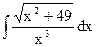 |
| 3. | 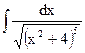 | 13. | 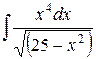 | 23. | 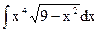 |
| 4. | 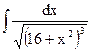 | 14. | 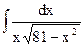 | 24. | 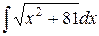 |
| 5. | 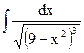 | 15. | 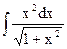 | 25. | 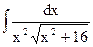 |
| 6. | 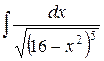 | 16. | 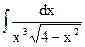 | 26. | 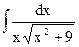 |
| 7. | 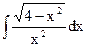 | 17. | 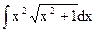 | 27. | 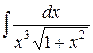 |
| 8. | 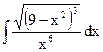 | 18. | 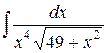 | 28. | 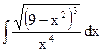 |
| 9. | 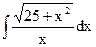 | 19. | 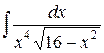 | 29. | 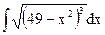 |
| 10. | 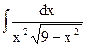 | 20. | 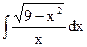 | 30. | 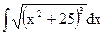 |
ЗАДАНИЕ 8
Вычислить неопределенные интегралы от тригонометрических функций.
| 1. | 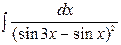 | 16. | 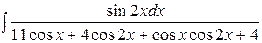 |
| 2. | 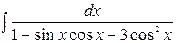 | 17. | 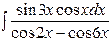 |
| 3. | 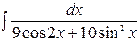 | 18. | 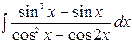 |
| 4. | 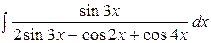 | 19. | 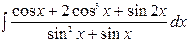 |
| 5. | 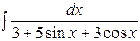 | 20. | 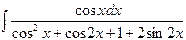 |
| 6. | 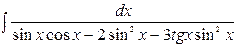 | 21. | 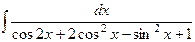 |
| 7. | 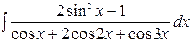 | 22. | 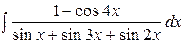 |
| 8. | 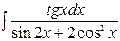 | 23. | 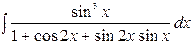 |
| 9. | 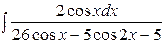 | 24. | 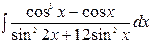 |
| 10. | 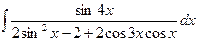 | 25. | 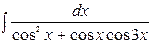 |
| 11. | 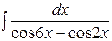 | 26. | 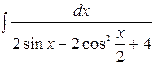 |
| 12. | 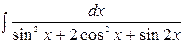 | 27. | 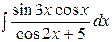 |
| 13. | 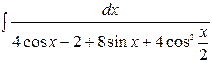 | 28. | 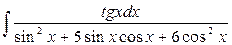 |
| 14. | 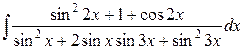 | 29. | 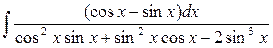 |
| 15. | 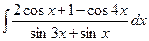 | 30. | 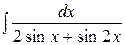 |
ПРИМЕР ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ
ПО ТЕМЕ «ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ»
1. Найти производную от функции
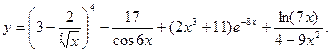
2. Найти производную 2-го порядка от функции 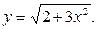
3. Написать уравнение касательной и нормали к кривой 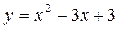 в точке х = 1. Построить кривую, касательную и нормаль.
в точке х = 1. Построить кривую, касательную и нормаль.
4. Зная уравнение движения точки 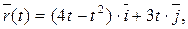 определить ее траекторию и найти векторы скорости и ускорения в момент времени t = 1.
определить ее траекторию и найти векторы скорости и ускорения в момент времени t = 1.
5. Найти предел
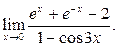
6. Исследовать функцию на экстремум (2-й вариант: найти наименьшее и наибольшее значения функции на отрезке):
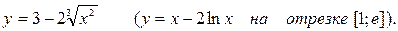
ПРИМЕР ВАРИАНТА КОНТРОЛЬНОЙ РАБОТЫ
ПО ТЕМЕ «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ»
Вычислить неопределенные интегралы:
1. 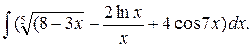
2. 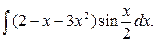
3. 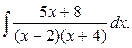
4. 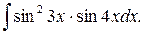
5. 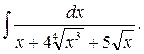
Вычислить площадь фигуры, ограниченной линиями:
6. 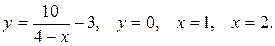
ВОПРОСЫ К ЭКЗАМЕНУ ПО ДИСЦИПЛИНЕ
«МАТЕМАТИЧЕСКИЙ АНАЛИЗ» (II семестр)
1. Понятие функции. Основные элементарные функции.
2. Предел функции. Два замечательных предела.
3. Непрерывность функции. Классификация точек разрыва.
4. Понятие производной, ее геометрический и механический смыслы.
5. Правила дифференцирования суммы, произведения и частного двух функций.
6. Таблица производных элементарных функций (ввод двух формул).
7. Производная сложной и обратной функций. Логарифмическое дифференцирование.
8. Уравнение касательной и нормали к графику функции в точке.
9. Дифференциал функции и его геометрический смысл. Дифференциалы высших порядков.
10. Производные высших порядков, механический смысл второй производной.
11. Основные теоремы дифференциального исчисления (Ролля, Лагранжа, Коши).
12. Правило Лопиталя.
13. Уравнения линий в параметрической форме (окружность, эллипс, циклоида). Производные параметрически заданных функций.
14. Функции, заданные в неявной форме. Правило их дифференцирования.
15. Векторная функция скалярного аргумента и ее производные (механический смысл 1-й и 2-й производных).
16. Исследование функции. Необходимое и достаточное условия экстремума.
17. Исследование функции. Выпуклость графика функции, точки перегиба.
18. Асимптоты графика функции.
19. Кривизна и радиус кривизны кривой.
20. Формула Тейлора.
21. Наибольшее и наименьшее значения непрерывной функции на отрезке.
22. Первообразная функция, ее свойства. Неопределенный интеграл, свойства.
23. Интегрирование заменой переменной и по частям. Примеры.
24. Рациональные функции. Интегрирование простейших дробей.
25. Интегрирование рациональных функций. Разложение правильной дроби на простейшие.
26. Интегрирование тригонометрических выражений. Примеры.
27. Интегрирование иррациональных выражений. Примеры.
28. Определенный интеграл. Задачи, приводящие к понятию определенного интеграла.
29. Определение операции интегрирования функции на отрезке. Свойства определенного интеграла.
30. Определенный интеграл Ньютона, его связь с определенным интегралом Римана.
31. Вычисление определенного интеграла с помощью замены переменной и по частям.
32. Несобственные интегралы I-го рода. Примеры.
33. Несобственные интегралы II-го рода. Примеры.
34. Применение определенного интеграла для вычисления площади плоской фигуры. Примеры.
35. Вычисление длины дуги плоской кривой. Дифференциал дуги. Примеры.
36. Вычисление объема тела с заданной площадью поперечного сечения. Объем тела вращения. Примеры.
37. Площадь поверхности вращения. Примеры.
38. Механические приложения определенного интеграла (центр масс, статические моменты, моменты инерции плоской фигуры).
39. Приближенное вычисление определенного интеграла (формула прямоугольников, трапеций, Симпсона).
