Лекция 20. Синтез систем управления
Существуют два основных принципа синтеза систем управления:
- построение системы с обеспечением заданных требований к показателям ее качества;
- построение системы, характеристики которой оптимальны в некотором смысле.
Для реализации первого принципа известны различные методы:
- корневой метод;
- метод корневого годографа;
- метод стандартных переходных характеристик;
- метод логарифмических амплитудных характеристик.
Для реализации второго принципа используется математический аппарат вариационного исчисления и принцип максимума или метод динамического программирования.
Подробно рассмотрим метод логарифмических амплитудных характеристик, наиболее широко применяемый на практике.
Основной вариант этого метода основан на использовании асимптотической ЛАХ разомкнутой системы. При этом система должна быть минимально-фазовой, то есть передаточная разомкнутой системы не должна содержать нулей (корней числителя) и полюсов (корней знаменателя) в правой полуплоскости.
Процесс синтеза в соответствии с методом ЛАХ включает в себя следующие основные этапы:
1. Построение исходной ЛАХ L(w) – асимптотической ЛАХ разомкнутой нескорректированной системы, включающей в себя объект управления, устройство управления, соответствующее цели управления, но, возможно, не обеспечивающее требуемого качества, необходимые измерительные устройства. Пример – следящая система с П-регулятором.
2. Построение желаемой ЛАХ Lж(w) на основе требований к показателям качества системы.
3. Нахождение асимптотической ЛАХ последовательного корректирующего устройства:
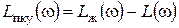 .
.
4. Получение на основе Lпку(w) передаточной функции корректирующего устройства и выбор способа его реализации: в виде дополнительного звена в прямой цепи (ПКУ), эквивалентного параллельного корректирующего звена, обратной связи или построение нового устройства управления, возможно, компьютерного.
При построении желаемой ЛАХ, рассматриваются требования к точности, быстродействию и запасу устойчивости системы.
Требования к точности определяют вид и характеристики желаемой ЛАХ на низких частотах.
Заданное значение времени переходного процесса (требование к быстродействию) позволяет выбрать величину частоты среза желаемой ЛАХ.
Участок ЛАХ в окрестности частоты среза называют среднечастотным.
Требования к запасу устойчивости определяют вид и характеристики желаемой ЛАХ на средних частотах.
Вспомним приближенное соотношение для оценки точности системы при гармоническом входном сигнале 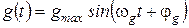 :
:
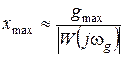 , (20.1)
, (20.1)
где xmax – амплитуда сигнала ошибки, W(jw) – частотная передаточная функция разомкнутой системы.
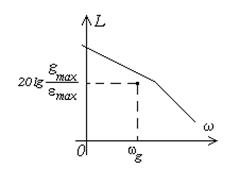 Рисунок 11. Рисунок 11. |
Формула (20.1) позволяет установить требования к низкочастотной части ЛАХ разомкнутой системы. Для того, чтобы максимальная ошибка замкнутой системы при гармоническом воздействии не превышала заданного значения emax, ЛАХ разомкнутой системы должна проходить выше контрольной точки с координатами (рисунок 11):
w = wg , 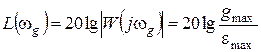 .(20.2)
.(20.2)
В общем случае требования к точности системы включают в себя требуемый порядок астатизма и допустимую амплитуду сигнала ошибки emax для входного сигнала произвольного вида, в том числе случайного.
Первое требование определяет наклон первого участка асимптотической ЛАХ: для астатизма 1-го порядка -20 дБ/дек, 2-го порядка -40 дБ/дек и так далее.
Второе требование можно учесть, если известны максимально возможные значения первой производной (скорости) 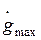 и второй производной (ускорения)
и второй производной (ускорения) 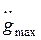 входного сигнала. Для заданных значений этих характеристик можно подобрать эквивалентный гармонический сигнал
входного сигнала. Для заданных значений этих характеристик можно подобрать эквивалентный гармонический сигнал 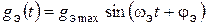 из условий:
из условий: 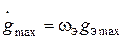 и
и 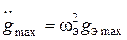 . В результате можно получить:
. В результате можно получить:
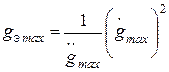 ,
, 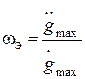 . (20.3)
. (20.3)
Теперь при заданной максимальной допустимой ошибке emax в соответствии с (20.2) могут быть получены координаты контрольной точки:
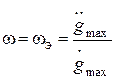 ,
, 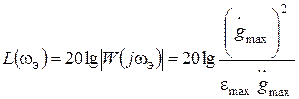 .
.
Если для эквивалентного гармонического сигнала предположить, что 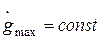 , а
, а 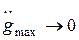 , то при уменьшении
, то при уменьшении 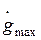 в 10 раз эквивалентная частота уменьшится в 10 раз, а значение L(wэ) увеличится на 20 дБ, то есть контрольная точка будет смещаться влево по прямой с наклоном -20дБ/дек.
в 10 раз эквивалентная частота уменьшится в 10 раз, а значение L(wэ) увеличится на 20 дБ, то есть контрольная точка будет смещаться влево по прямой с наклоном -20дБ/дек.
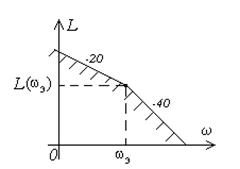 Рисунок 12. Рисунок 12. |
Если же предположить, что 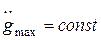 , а
, а 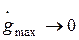 , то аналогично можно показать, что контрольная точка будет смещаться вправо по прямой с наклоном - 40 дБ/дек.
, то аналогично можно показать, что контрольная точка будет смещаться вправо по прямой с наклоном - 40 дБ/дек.
Область, расположенная ниже двух таких прямых должна рассматриваться как запретная область для ЛАХ синтезируемой системы (рисунок 12). Это обеспечит заданную точность при известных максимальных значениях скорости и ускорения входного сигнала.
Полученной запретной области может соответствовать только астатическая система. Если, как поступают в большинстве случаев, совместить низкочастотную часть желаемой ЛАХ с границей запретной области, получим систему с астатизмом первого порядка, коэффициент передачи которой (добротность по скорости) можно рассчитать по координатам контрольной точки:
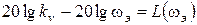 ,
, 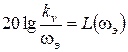 ,
,
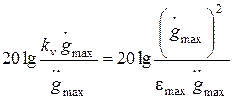 ,
, 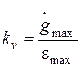 .
.
Если астатизм не требуется, то форму границы запретной области можно уточнить, если принять ограничение не только на скорость и ускорение, но и на величину задающего воздействия gmax.
Подберем эквивалентный гармонический сигнал из условий: 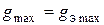 ,
, 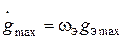 . Тогда при заданной допустимой ошибке emax получим контрольную точку с координатами:
. Тогда при заданной допустимой ошибке emax получим контрольную точку с координатами:
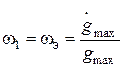 ,
, 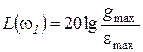 .
.
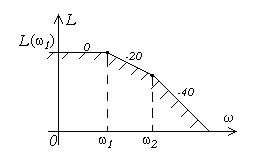 Рисунок 13. Рисунок 13. |
Если уменьшать 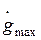 при постоянной gmax, контрольная точка будет сдвигаться влево по горизонтальной прямой на уровне
при постоянной gmax, контрольная точка будет сдвигаться влево по горизонтальной прямой на уровне 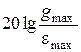 , а при уменьшении gmax при постоянной
, а при уменьшении gmax при постоянной 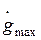 - вправо по прямой с с наклоном -20дБ/дек, пока будет выполняться условие
- вправо по прямой с с наклоном -20дБ/дек, пока будет выполняться условие 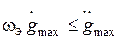 . Далее следует воспользоваться полученными выше результатами. После частоты
. Далее следует воспользоваться полученными выше результатами. После частоты 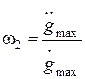 получим прямую с наклоном - 40дБ/дек. Таким образом, если не требуется обеспечить астатизм системы, то при условии ограничения максимальной величины задающего воздействия запретная область для ЛАХ разомкнутой системы будет иметь вид, показанный на рисунке 13.
получим прямую с наклоном - 40дБ/дек. Таким образом, если не требуется обеспечить астатизм системы, то при условии ограничения максимальной величины задающего воздействия запретная область для ЛАХ разомкнутой системы будет иметь вид, показанный на рисунке 13.
Требования к запасу устойчивости системы в рамках метода ЛАХ задаются в форме максимально допустимой величины показателя колебательности.
По заданному значению M=Mmax на рисунке 14 построена запретная область для амплитудно-фазовой частотной характеристики (рисунок 14а) или ЛФЧХ (рисунок 14б) разомкнутой системы.
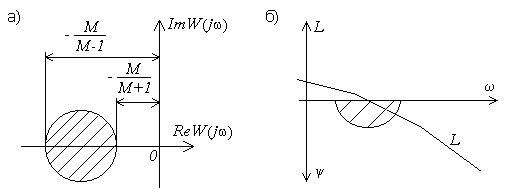 Рисунок 14. Рисунок 14. |
Для рисунке 14б границы запретной области вдоль оси частот соответствуют расстояниям от начала координат до точек пересечения окружности (рисунок 14а) с отрицательной вещественной полуосью:
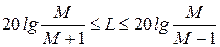 .
.
Учитывая, что для минимально-фазовой системы вид асимптотической ЛАХ однозначно определяет передаточную функцию, а значит и фазо-частотную характеристику, нетрудно убедиться, что для обеспечения сколько-нибудь приемлемого запаса устойчивости нельзя допустить, чтобы ЛАХ на частоте среза имела наклон -40 Дб/дек. Следовательно, при переходе к средним частотам желаемая ЛАХ должна изменить наклон. Типовой участок средних частот для желаемой ЛАХ показан на рисунке 15. Ему соответствует передаточная функция
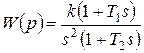 ,
, 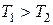 .
.
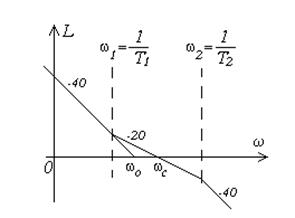 Рисунок 15. Рисунок 15. |
Базовая частота связана с коэффициентом передачи соотношением: 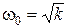 , а частота среза определяется через базовую частоту:
, а частота среза определяется через базовую частоту: 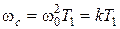 .
.
Для обеспечения заданного значения показателя колебательности M длина участка ЛАХ с наклоном -20дБ/дек должна составлять не менее:
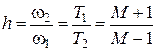 .
.
Рекомендуемые значения постоянных времени определяются соотношениями:
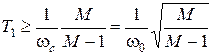 , (20.4)
, (20.4)
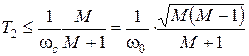 . (20.5)
. (20.5)
При неравенствах в (20.4)-(20.5) обеспечивается дополнительный запас устойчивости, и показатель колебательности имеет меньшее значение.
Если в системе присутствуют другие инерционные звенья с меньшими постоянными времени, например:
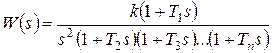 ,
,
постоянная времени T1 должна удовлетворять соотношению (20.4), а остальные постоянные времени должны удовлетворять неравенству:
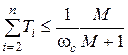 .
.
При синтезе желаемой ЛАХ возможен учет требования к запасу устойчивости в форме допустимого значения перерегулирования. В этом случае применяются специальные номограммы, также позволяющие выбрать протяженность участка ЛАХ с наклоном -20дБ/дек.
В любом следует иметь в виду закономерность: увеличение протяженности участка ЛАХ с наклоном -20 дБ/дек приводит к повышению запаса устойчивости системы, то есть к уменьшению значений показателя колебательности и перерегулирования, а также к увеличению запаса устойчивости по фазе.
Вернемся к примеру следящей системы, рассмотренному на лекции 2. Передаточная функция исходной разомкнутой системы:
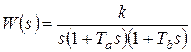 , k=10; Ta=10; Tb=0,2.
, k=10; Ta=10; Tb=0,2.
Главная обратная связь – единичная. Требуется синтезировать корректирующее устройство, обеспечивающее emax=0,1; M=1,5 при 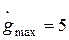 и
и 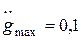 . Выполнить сравнительный анализ качества исходной и скорректированной систем.
. Выполнить сравнительный анализ качества исходной и скорректированной систем.
Проверим устойчивость исходной системы алгебраическим способом: D(s)47=TaTbs3+(Ta+Tb)s2+s+k; 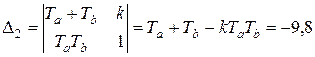 . Исходная система неустойчива.
. Исходная система неустойчива.
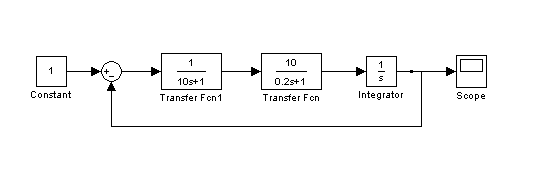
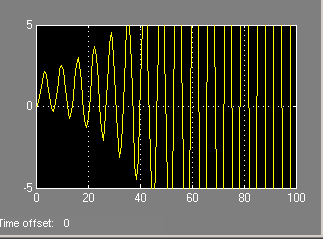
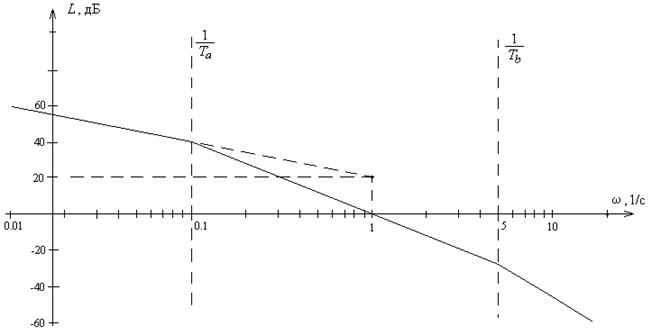
На рисунках представлены модель исходной системы в Simulink и ее переходная характеристика, демонстрирующая неустойчивость системы, а также исходная ЛАХ системы.
Найдем частоту эквивалентного гармонического сигнала 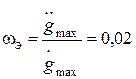 и вертикальную координату контрольной точки:
и вертикальную координату контрольной точки: 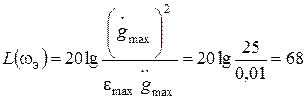 Дб.
Дб.
На рисунке представлена запретная область для низкочастотной части ЛАХ, соответствующая требованиям к точности системы.
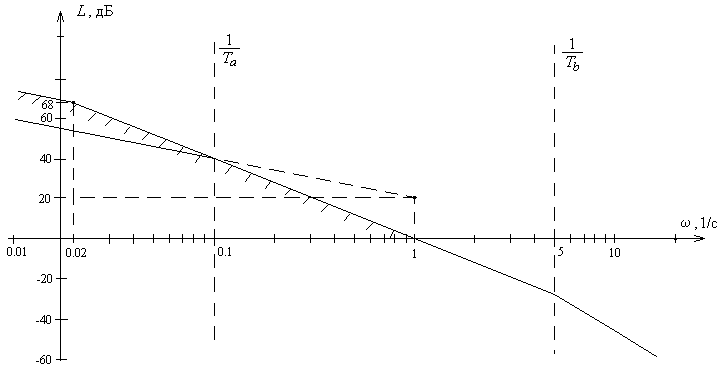
Видно, что исходная ЛАХ не удовлетворяет этим требованиям. Для их выполнения необходимо сместить ЛАХ вверх до границы запретной области, то есть поднять на 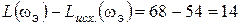 Дб, что соответствует введению в систему дополнительного усилителя с коэффициентом усиления kдоп=5. Таким образом, итоговый коэффициент усиления синтезируемой системы составит: kж=k.kдоп=50.
Дб, что соответствует введению в систему дополнительного усилителя с коэффициентом усиления kдоп=5. Таким образом, итоговый коэффициент усиления синтезируемой системы составит: kж=k.kдоп=50.
Исходная для синтеза корректирующего устройства ЛАХ 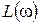 проходит по участку границы запретной области с наклоном -20 (рисунок).
проходит по участку границы запретной области с наклоном -20 (рисунок).
Желаемая ЛАХ на низких частотах проходит по границе запретной области, то есть отклоняется от исходной и меняет наклон на -40 на сопрягающей частоте wэ.
Для средних частот длина участка желаемой ЛАХ, пересекающего горизонтальную ось с наклоном -20, составляет 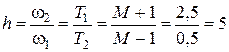 , или 0,7 декады. Найдем постоянные времени и сопрягающие частоты, определяющие его границы, с учетом w0=1 (рисунок):
, или 0,7 декады. Найдем постоянные времени и сопрягающие частоты, определяющие его границы, с учетом w0=1 (рисунок):
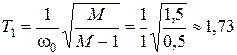 ;
; 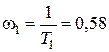 ;
;
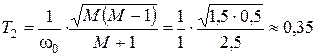 ;
; 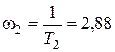 .
.
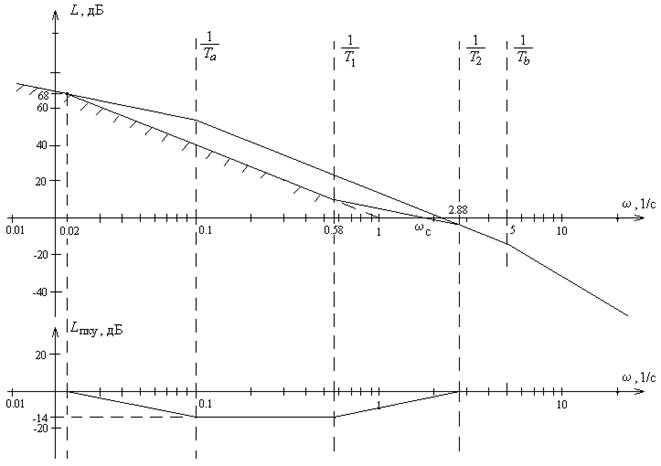
Внизу на рисунке представлена асимптотическая ЛАХ последовательного корректирующего устройства, полученная по соотношению: 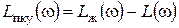 . Соответствующая ей передаточная функция имеет вид:
. Соответствующая ей передаточная функция имеет вид: 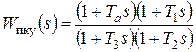 , где
, где 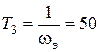 .
.
Передаточная функция разомкнутой синтезированной системы соответствует желаемой ЛАХ: 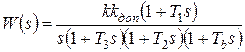 . Определим для нее частоту среза
. Определим для нее частоту среза 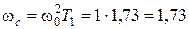 и запас устойчивости по фазе:
и запас устойчивости по фазе:
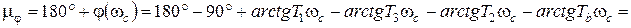
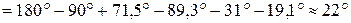 .
.
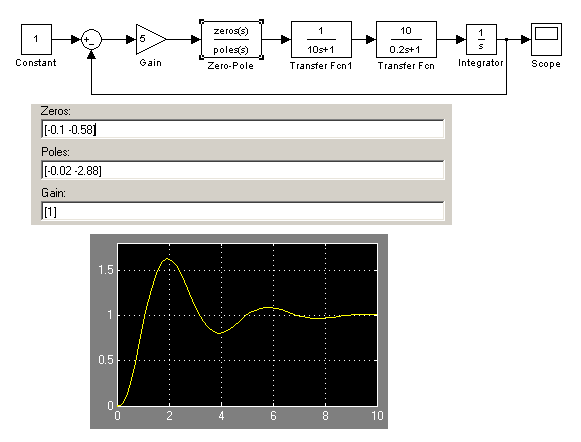
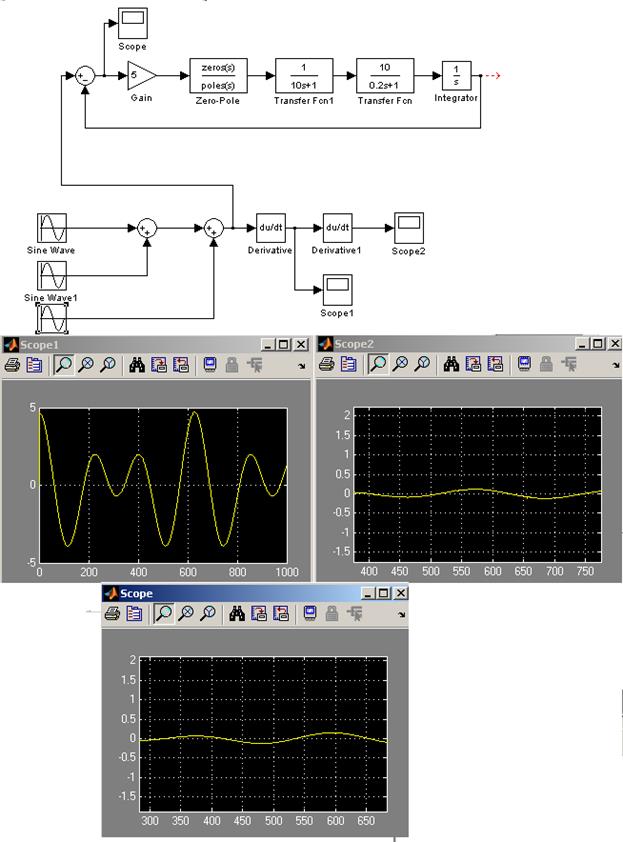
На рисунке представлены модель скорректированной системы в Simulink и ее переходная характеристика, демонстрирующая перерегулирование немногим более 60%.
Для проверки выполнения требований к точности системы проведем моделирование с полигармоническим входным сигналом с заданными 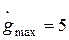 и
и 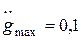 (
( 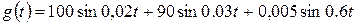 ) и убедимся, что амплитуда сигнала ошибки не превышает заданной допустимой величины (рисунок).
) и убедимся, что амплитуда сигнала ошибки не превышает заданной допустимой величины (рисунок).
Наиболее распространенные корректирующие звенья последовательного типа и их характеристики представлены в таблице 1.
Таблица 1
| Математическая модель | Частотные характеристики | Техническая реализация |
Дифференцирующее 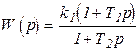 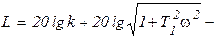 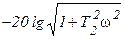 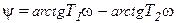 | 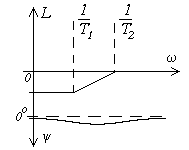 | 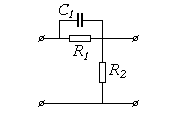 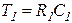 , , 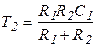 , , 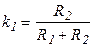 |
Интегрирующее 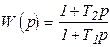 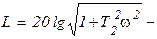 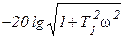 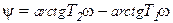 | 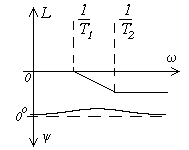 | 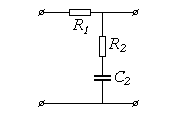 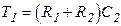 , , 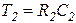 |
Интегро-дифференцирующее 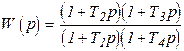 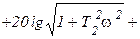 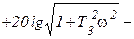 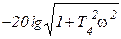 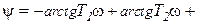 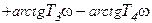 | 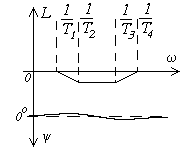 | 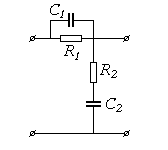 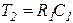 , , 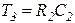 , , 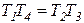 , , |
Антивибратор 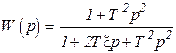 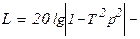 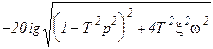 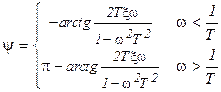 | 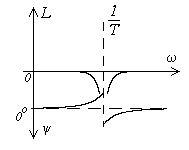 | 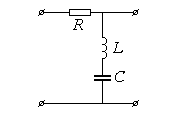 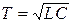 , , 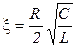 |
На практике далеко не всегда удается построить требуемое ПКУ или оно оказывается неоправданно сложным.
Непрерывные корректирующие звенья вводятся в состав системы тремя способами:
- последовательные корректирующие звенья (рисунок 17а);
- параллельные корректирующие звенья (рисунок 17б);
- гибкие отрицательные обратные связи (рисунок 17в).
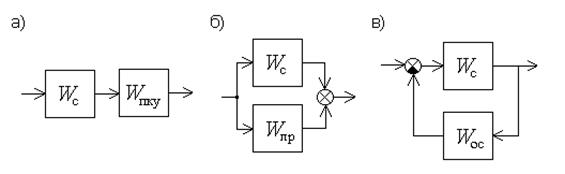 Рисунок 17. Рисунок 17. |
Здесь 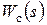 - звено, входящее в состав непрерывной части корректируемой системы.
- звено, входящее в состав непрерывной части корректируемой системы.
Использование того или иного типа корректирующих звеньев определяется удобством технической реализации. В линейных системах для корректирующего устройства одного типа всегда можно подобрать эквивалентное, то есть обеспечивающее для данной системы аналогичные динамические свойства, корректирующее устройство второго или третьего типа. Расчетные соотношения для получения передаточных функций эквивалентных корректирующих звеньев в соответствии с рисунком 17 можно получить на основе следующего равенства:
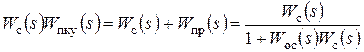 .
.
В результате получаются следующие соотношения:
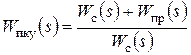 ,
, 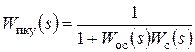 ,
,
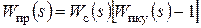 ,
, 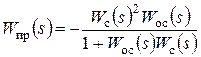 ,
,
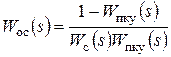 ,
, 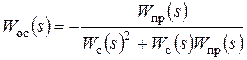 .
.
Последовательные корректирующие звенья удобно применять, когда в системе используется электрический сигнал, величина которого функционально связана с сигналом ошибки, без введения высокочастотных модулированных сигналов. Тогда последовательные корректирующие звенья могут быть построены в виде достаточно простых схем из резисторов, конденсаторов и катушек индуктивности.
Параллельные корректирующие звенья удобны, когда необходимо реализовать сложный закон управления с введением интегралов и производных от сигнала ошибки.
Достоинством обратных связей является обеспечение дополнительного эффекта уменьшения влияния нелинейностей и нестабильности характеристик охватываемой части системы на работу системы в целом.
