Вимірний арифметичний простір. Поняття, приклади і найпростіші властивості векторного простору.

ЛЕКЦІЯ № 6

Тема № 6. Лінійні простори та лінійні оператори.

з навчальної дисципліниЛінійна алгебра та аналітична геометрія

напряму підготовки УПРАВЛІННЯ ІНФОРМАЦІЙНОЮ БЕЗПЕКОЮ

освітньо-кваліфікаційного рівня БАКАЛАВР

Лекція розроблена

Кандидатом фізико-математичних наук Жихарєвою Ю.І.

Навчальна та виховна мета:

1. Студенти повинні знати теоретичні питання з теми «Лінійні простори та лінійні оператори»: означення лінійних просторів та лінійних операторів; лінійної залежності та незалежності векторів, означення базису векторів, алгоритм розкладання вектора за базисом; власні значення та власні вектори лінійного оператора та алгоритм їх знаходження.

2. Студенти повинні вміти визначати лінійну незалежність векторів, розкладати вектори за базисом, знаходити власні значення та власні вектори лінійного оператора.

3.Розвиток мислення студентів, залучення до вивчення математики, як необхідної складової фахівця технічного університету

План.

1. 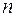-вимірний арифметичний простір. Поняття, приклади і найпростіші властивості векторногопростору.

2.Лінійна залежність системи векторів. Базис і розмірність векторного простору.

3.Координати вектора у векторному просторі. Розкладання вектора за базисом.

4.Лінійний оператор та його матриця.

5.Власні значення і власні вектори лінійного оператора.

ЛІТЕРАТУРА:

1. Барковський В.В., Барковська Н.В. Вища математика для економістів. – К.: ЦУЛ, 2002 – 401 с.

2. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – Москва: Наука, – 1988 – 240 с.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Ч 1-2. Москва.: Высшая школа, 1986.

4. Кривуца В.Г., Барковський В.В., Барковська Н.В. Вища математика. Практикум. - К.:ЦУЛ, 2003 – 536 с.

5. Овчинніков П.Ф., Яремчик Ф.П., Михайленко В.М. Вища математика. – К.: Техніка, ч.І 596 с., ч.ІІ 792 с., 2000.

Конспект лекції

вимірний арифметичний простір. Поняття, приклади і найпростіші властивості векторного простору.

Нехай 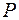– числова множина дійсних або комплексних чисел. Числа з цієї множини будемо позначати малими латинськими буквами.

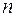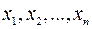Означення. Будь-який впорядкований набір з чисел з множини 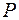називається 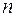-вимірним числовим вектором. Числа 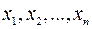називаються координатами або компонентами вектора. Позначається .

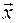Означення. Два числових вектори 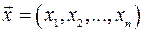та 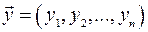рівні тоді і тільки тоді, коли рівні їх відповідні компоненти:

.

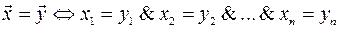Відзначимо, що два числових вектори не можуть бути рівні, якщо число компонент в них неоднакове.

Означення. Сумою векторів 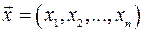та 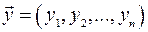називається вектор

.

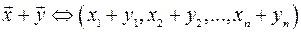Означення. Добутком вектора 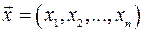на число 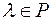називається вектор

.

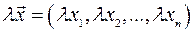Означення. Множина 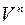всіх 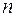-вимірних числових векторів з компонентами з множини 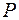разом з введеними операціями додавання векторів і множення вектора на число з 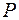, для яких виконуються всі властивості лінійних дій над векторами, називається 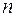-вимірним арифметичним простором над полем .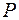