Стационарлы марковтық дереккөздерді кодтау
Ең әуелі 5.2.1 теоремада қалыптасқан дереккөздерді кодтау теоремасын еске алайық. Бұл теоремада L символды блоктар қаралған. Теорема бойынша L шексіздікке ұмтылған жағдайда L ұзындықты блоктар үшін кодты сөзінің орташа ұзындығы бір символға бірлескен 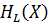 энтропияға жақын префиксті код бар.
энтропияға жақын префиксті код бар.
r жадты марковтық дереккөздің жағдайында, блокқа арналған L = r ұзындықты бірлескен энтропия шекті жағдай болып табылады және кодтау теоремасы келесі түрде қалыптасуы мүмкін:
Теорема 5.5.1.r жадты және 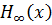 энтропиялы стационарлы марковтық дереккөздер үшін кодтау теоремасы.
энтропиялы стационарлы марковтық дереккөздер үшін кодтау теоремасы.
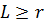 ұзындықты блок үшін кодты сөзінің орташа
ұзындықты блок үшін кодты сөзінің орташа 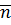 ұзындығы келесі теңсіздікті қанағаттандыратын D-типті префиксті код бар.
ұзындығы келесі теңсіздікті қанағаттандыратын D-типті префиксті код бар.
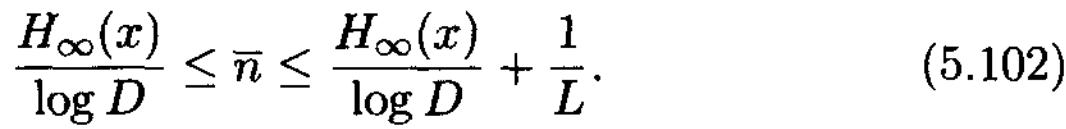
Марковтық дереккөздің жадсыз кіші дереккөздерге бөлінуінен оптималды кодтау стратегиясы пайда болады.
Егер бастапқы ахуалдар мағлұм болса, онда дереккөздерді кодтау уақтысында келесі ахуалдар біріңғай анықталған болады. Сонымен бірге, тасымалдағышта және қабылдағышта әрбір көпшілік кіші дереккөздер үшін ахуалдар және символдардың ықтималдықтарының бөлінуін ескере отырып кодтау және декодтау жүргізуге болады.
Хаффман кодтарының практикалық жүзеге асуы ауқымды кодтық ұтысқа жету үшін дерліктей үлкен ұзындықты блоктарды кодтау қажет екенін көрсетеді. Мұнан басқа, кәдімгі ахуалдар әрдайым r символдармен анықталуы қажет, себебі үлкен ұзындықты блоктарға өту күрделі болмауы керек.
Ұсынылып отырған қарапайым стратегия дереккөздің жадын толық ескереді, және шекті жағдайда, оптималды префиксті кодты алуға мүмкіндік береді.
r жадты және 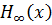 энтропиялы стационарлы марковтық X дереккөзді кодтау.
энтропиялы стационарлы марковтық X дереккөзді кодтау.
1. Дереккөздің 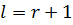 символдарын блоктарға біріктіру.
символдарын блоктарға біріктіру.
2. Блоктар үшін Хаффман кодтауын жүргізу.
3. Егер символ үшін кодты сөздің орташа ұзындығы 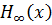 энтропиясы-
энтропиясы-
нан дерліктей өзгешеленетін болса, онда келесі символдардың есебінен блоктың ұзындығын жоғарылату. Үлкен ұзындықты блоктар үшін Хаффман кодтауын жүргізу. Бұл процессті кодты сөздің орташа ұзындығының энтропияға жақындағанына дейін жалғастыру.
Мысал:r = 2 жадты стационарлы марковтық дереккөзді кодтау (жалғасы).
Ұсынылған алгоритмнің нәтижелілігін алдыңғы бөлімдердегі сандық мысалда тексереміз.
Дереккөздің r = 2 жадысына сәйкес, дереккөздің әр үш символын блокқа біріктіреміз және Хаффман кодтауын жүргіземіз.
Блоктар үшін қажетті ахуалдар ықтималдығы ықтималдықтардың стационарлы бөлінуімен (5.58) және өтпелі ықтималдықтар матрицасымен (5.58) я болмаса ахуалдар кестесімен (5.7 сурет) анықталады.
Мәселен, 001 блогының ықтималдығы тең болады
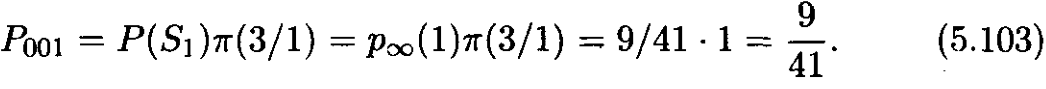
000 блогы ешқашан пайда болмайтынына назар салайық, демек оны кодтау-дың да қажеті жоқ.
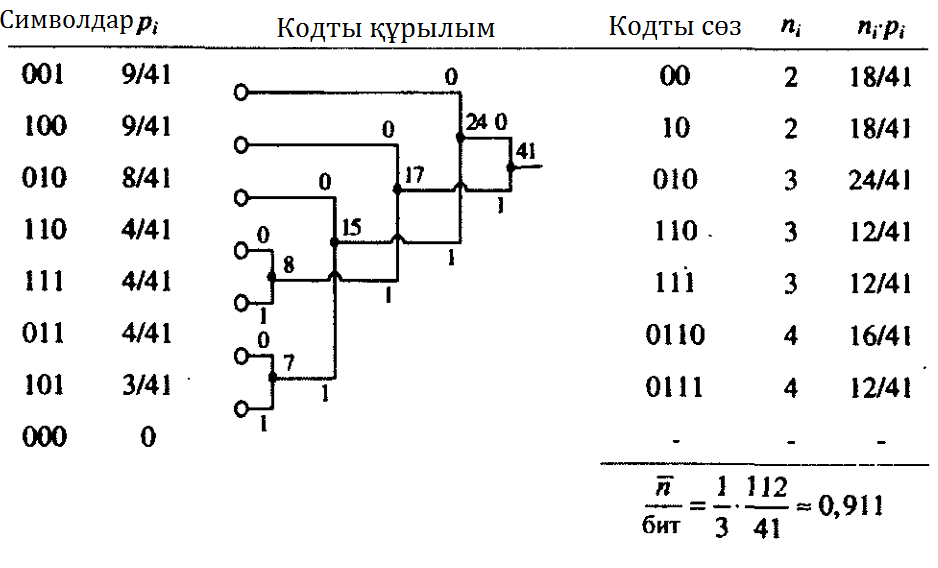
5.1 кестеден символ үшін кодты сөздің орташа ұзындығы 0,911-ге тең екенін білеміз. Сол себепті кодтау нәтижелілігі дерліктей аз
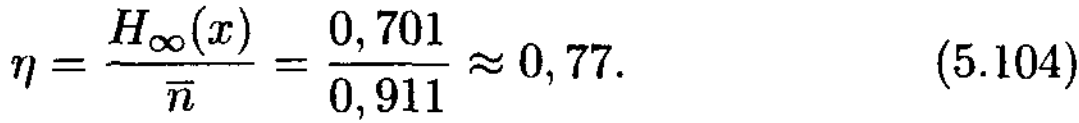
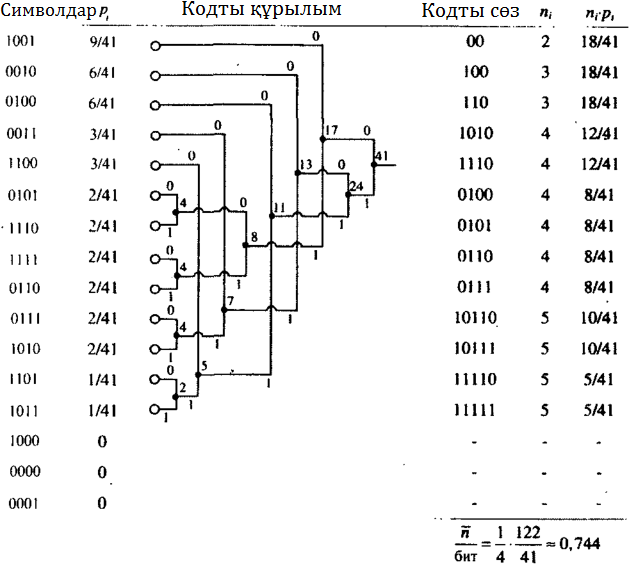
Үлкен ұзындықты блоктарды құрумен кодтау нәтижелілігі дерліктей көбеюі мүмкін. Ұзындықтары 4-ке тең блоктар үшін (5.2 кесте) Хаффман кодтауын қайталайық. 5.1 кестеден символ үшін кодты сөздің орташа ұзындығы 0,744 екенін көреміз. Кодтау нәтижелілігі енді
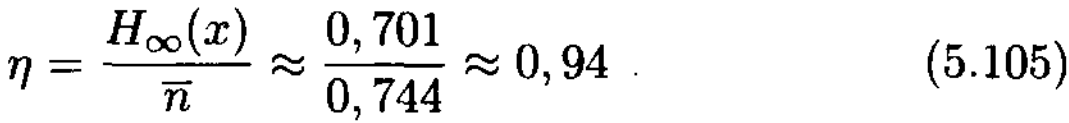
және біз, негізінде, кодтау мүмкіндіктерінің біршама бөлігін жүзеге асырдық, бірақ, блок ұзындығын тағы да жоғарылатумен кодтаудан ұтысты көбейтуге болады.
Мысал:Бірінші тәртіпті марковтық дереккөз.
5.9 суретте бірінші тәртіпті марковтық дереккөздің ахуалдар кестесі көрсетілген.
1. 5.9 суреттің жетіспейтін ықтималдықтарын толықтырыңыз және ахуалдар ықтималдықтарының стационарлы бөлінуін табыңыз.
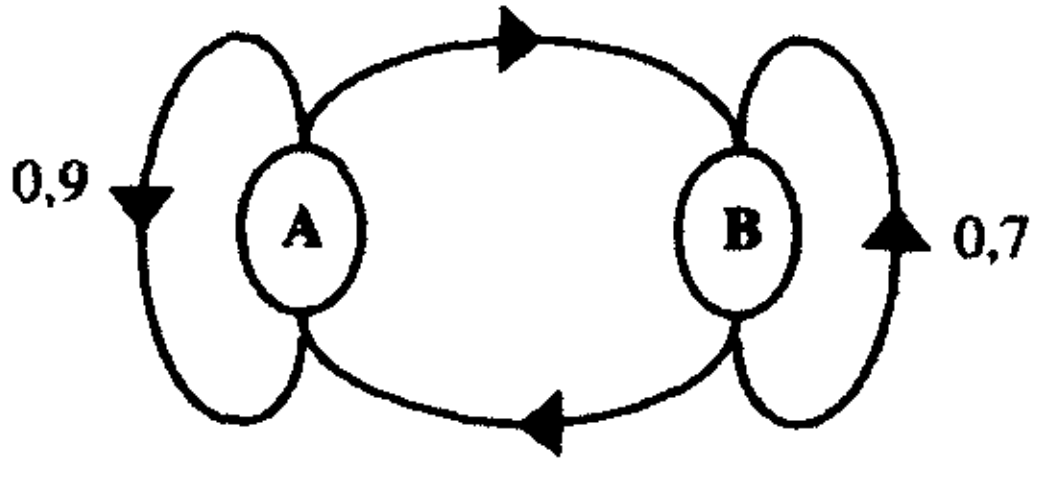
5.9 Сурет.Бірінші тәртіпті марковтық дереккөздің ахуалдар кестесі.
5.1 Кесте.r = 2 жадты және блок ұзындығы 3–ке тең марковтық дереккөз
үшін Хаффман кодтауы
2. Дереккөздің энтропиясын табыңыз.
3. Үш екілік символдардан тұратын блоктар үшін Хаффман кодтауын жүргізіңіз.
4. Кодтау қандай нәтижелілікке ие?
Шешімі.
1. 5.9 суреттің өтпелі ықтималдықтары тең

А ахуалының ықтималдығының стационарлы мәні келесі теңдіктерге сәйкес анықталады
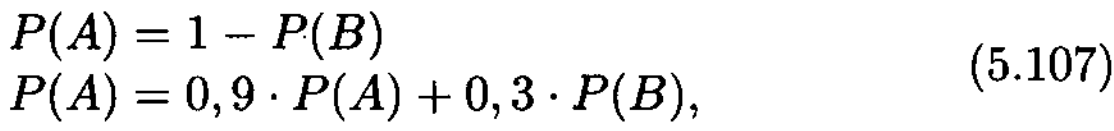
сондықтан,
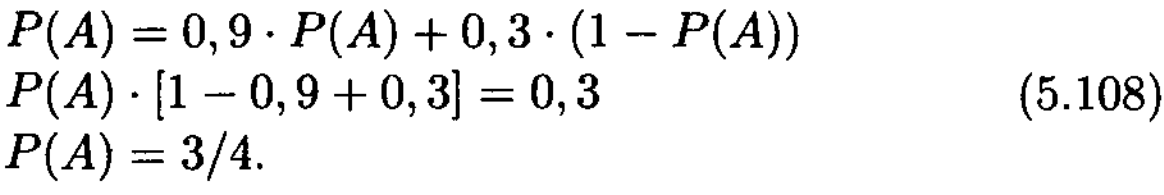
Мұнан шығатыны

5.2 Кесте.r = 2 жадты және блок ұзындығы 4–ке тең марковтық дереккөз
үшін Хаффман кодтауы
2. Дереккөз энтропиясының анықталуы
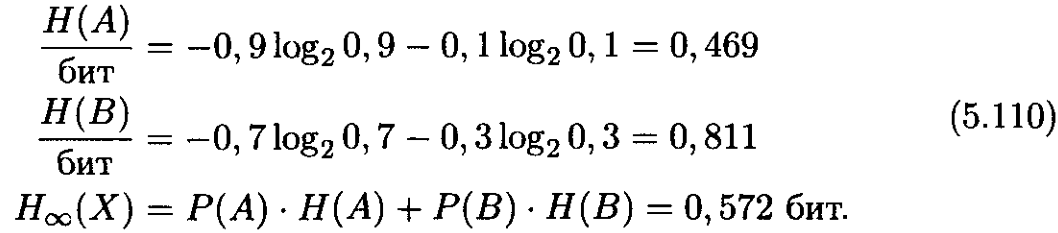
3. Үш екілік символдан тұратын блоктар ықтималдықтары
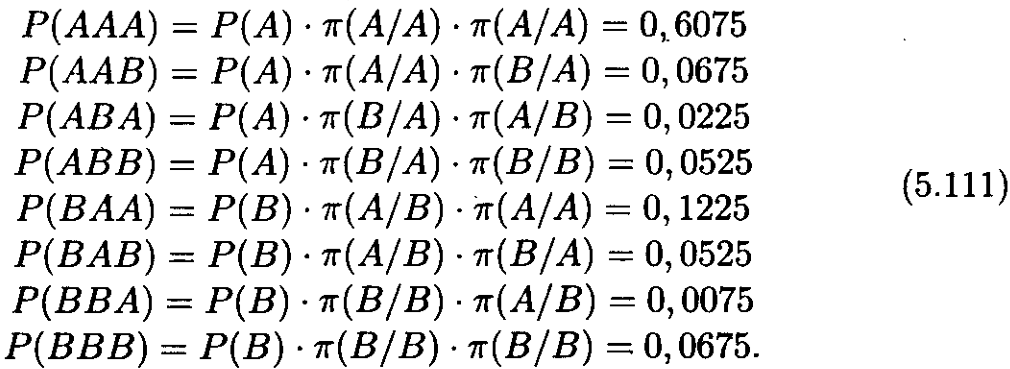
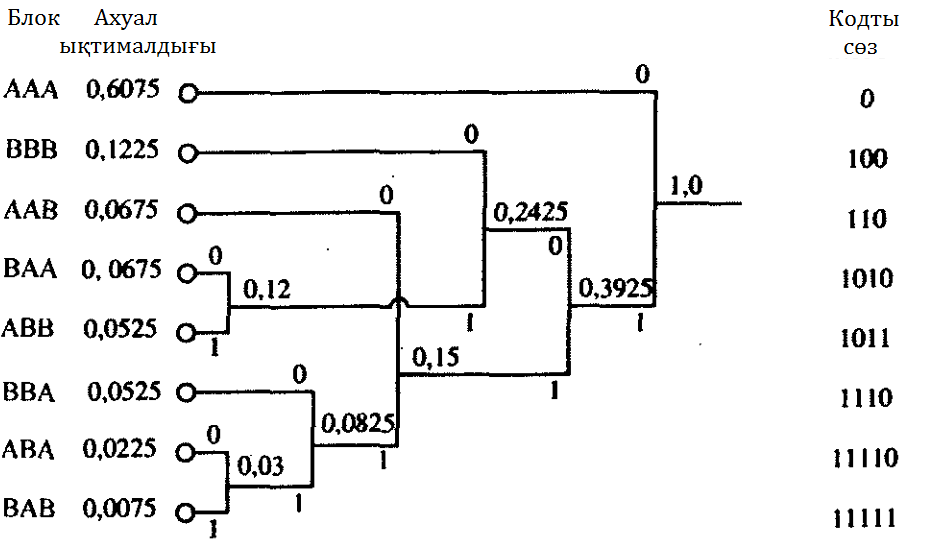
5.10 Сурет. Хаффман кодтауы.
4. Кодты сөздің орташа ұзындығы келесі түрде анықталады
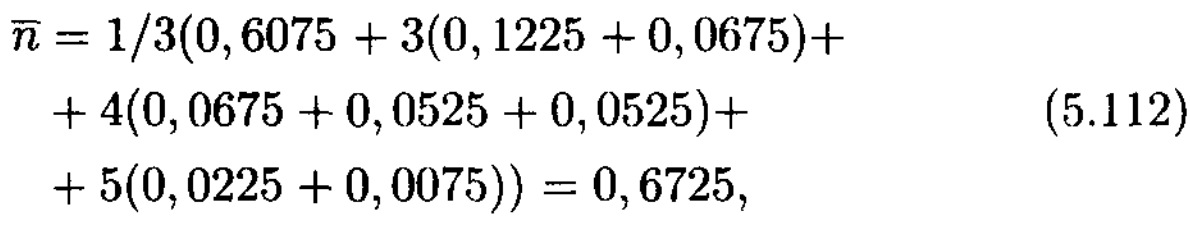
демек, кодтау нәтижелілігі тең болады
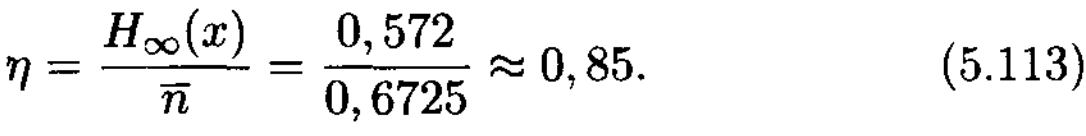
Орытындылар
Төменде келтірілген кестелерде оқырман маңызды бекітулерді және марковтық тізбектер мен марковтық дереккөздер арасындағы байланысты таба алады.
5.3 Кесте. Марковтық тізбектер.
| ● Марковтық процесс деп қазіргі мағлұм, ал болашақ өткенге тәуелді емес стохастикалық процессті айтамыз. |
● Ахуалдарда және уақытта дискретті марковтық процесс марковтық тізбек деп аталады. Ахуалдар реттілігі оның жүзеге асуы болып табылады 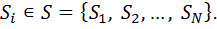 |
● Егер ахуалдар арасындағы өтпелі ықтималдықтар уақыттың санақ нүктесінің таңдауына тәуелді емес болса, Марковтың тізбегі гомогенді болып табылады, демек 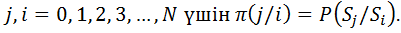 |
● Гомогенді Марковтық тізбек толықтай өтпелі ықтималдықтар П матрицасымен анықталады 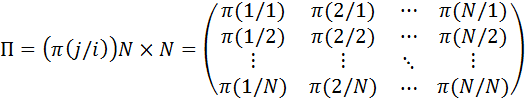 және бастапқы бөлінумен және бастапқы бөлінумен 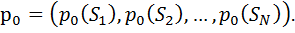 |
● Өтпелі ықтималдықтар матрицасының эквиваленті болып түйінді, жолды және ахуалдарға, ахуалдар арасындағы өткелдерге және өтпелі ықтималдықтарға сәйкес жолының салмағы бар ахуалдар кестесі болып табылады. 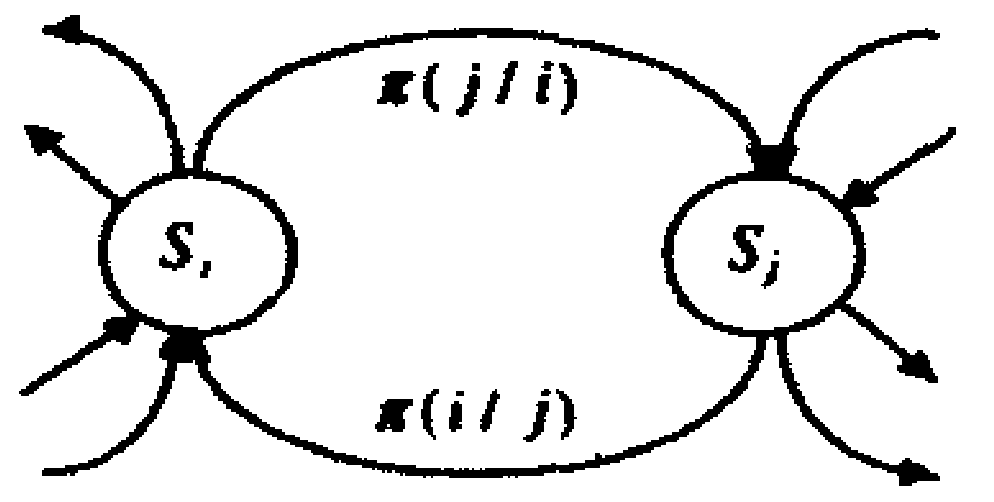 5.11 Сурет. 5.11 Сурет. |
● Гомогенді марковтық тізбектің n–ші қадамдағы ахуалдарының бөлінуі келесі түрде анықталады 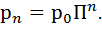 |
5.4 Кесте. Марковтық тізбектер. (жалғасы)
● Егер ахуалдардың бөлінуі уақытта тұрақты болса Марковтың гомогенді тізбегі стационарлы. Бұл жағдайда бастапқы бөліну өтпелі матрицаның меншікті векторы болып табылады, яғни 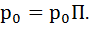 |
● Егер шек бар болса, Марковтың гомогенді тізбегі тұрақты 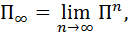 сонымен бірге, сонымен бірге, 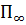 барлық қатарлары барлық қатарлары 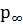 шекті бөлінуіне тең. шекті бөлінуіне тең. |
● 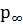 шекті бөлінуі Марковтың тұрақты тізбегінің жалғыз стационарлы бөлінуі болып табылады. шекті бөлінуі Марковтың тұрақты тізбегінің жалғыз стационарлы бөлінуі болып табылады. |
5.5 Кесте. Стационарлы Марковтық дереккөздер.
Шекті дискретті r жадты марковтық дереккөз толықтай келесі шарттармен анықталады: ● Бос емес 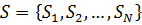 ахуал көпшілігі берілген, сонымен бірге, S r ұзындығының барлық векторларын қамтиды; ● Әрбір ахуал көпшілігі берілген, сонымен бірге, S r ұзындығының барлық векторларын қамтиды; ● Әрбір 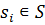 ахуалы ахуалы 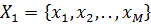 алфавитті және алфавитті және 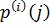 алфавитінің j символдың ықтималдықтары бар жадсыз дискретті дереккөзге сәйкес келеді; ● r ретті символды және келесі алфавитінің j символдың ықтималдықтары бар жадсыз дискретті дереккөзге сәйкес келеді; ● r ретті символды және келесі 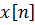 символы жаңа символы жаңа 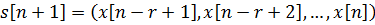 ахуалын құрайтын ахуалын құрайтын 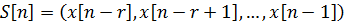 ахуалы; ● Ахуалдардың бастапқы бөлінуі берілген ахуалы; ● Ахуалдардың бастапқы бөлінуі берілген 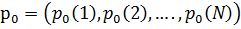 . . |
r жадты стационарлы марковтық дереккөздің энтропиясы кіші дереккөздердің шартты энтропияларының математикалық күтімі ретінде анықталады 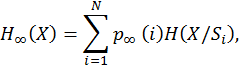 сонымен қатар, i ахуалына сәйкес i-ші кіші дереккөздің шартты энтропиясы тең болады сонымен қатар, i ахуалына сәйкес i-ші кіші дереккөздің шартты энтропиясы тең болады 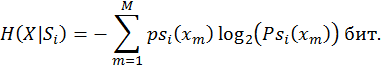 |
БӨЛІМ
ДЕРЕКТЕРДІ
ЫСУ
Кіріспе
Деректерді қысудың мақсаты дереккөздерді оптималды кодтау тәсілімен ақпаратты сақтауға немесе тасымалдауға кететін техникалық шығынды минимизациялау болып табылады. Сонымен қатар, екі түсінікті ажыратады:
● Жоқ мағлұмат – бұл тасымалдағанда мән берілмейтін ақпарат. Мысал ретінде дәстүрлі телефонияны келтіруге болады. Телефондық каналдарда ақпарат тасымалдау 3,4 кГц тілкемде жүзеге асады. Барлық басқа спектральді құрамалар ескерілмейді, сонымен қатар тасымалданып жатқан ақпараттың біраз бөлігі жоғалып кетеді. Бастапқы сөйлемдік сигнал соңғы қабылдағышта толықтай қайта қалпына келуі мүмкін емес екендігі айдан анық. Бұл жағдайда шығыны бар кодтау жайлы айтамыз.
● Шығын дегеніміз хабарламада қабылдағыш үшін қажетті мағлұматтың бірнеше мәрте қайталануы. Шығынды ақпарат жоғалтусыз жоюға болады. Мысал ретінде Хаффман кодтауын келтіре аламыз. Мұндай кодтауды шығынсыз кодтау деп атайды.
Деректерді қысудың маңызды мысалы сандық радиохабарлама (Digital Audio Broadcasting, DAB) және сандық телевидение (Digital Video Broadcasting, DVB) болып табылады. Екі система да MPEG (Motion Pictures Expert Group) стандарттарын қолданатын аудио және видео сигналдарды кодтау негізінде жұмыс істейді. Аудиосигналды кодтау жасырын спектральді және уақыт эффектілерін қолданатын сөйлем қабылдаудың психологиялық үлгісінде негізделген, солай бола тұра сигналды блокта аудиосигналдың құлаққа есітілмейтін бөлігі (беймағлұм ақпарат) жойылады. Ұқсас эффекттер видеосигналды кодтау уақтысында да пайдаланылады (яғни қимылдың психологиялық әсері). Бейнелерді кодтау одан да жоғары қысу дәрежесіне жетуге мүмкіндік береді.
Қысу дәрежесі тасымалдау үшін шығынмен немесе ақпаратты 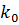 қысусыз сақтау және қандай-да бір
қысусыз сақтау және қандай-да бір 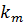 қысу әдісін пайдалану шығыны менен анықталады
қысу әдісін пайдалану шығыны менен анықталады

Қысу дәрежесі қолданылып жатқан алгоритмге және дереккөс қасиетіне байланысты. Практикада жететін қысу дәрежелерінің кейбір сандық мысалдарын келтірейік:
- 80%-ға дейін мәтіндік деректер үшін (ZIP қысу программасының көмегімен Word 97 редактор форматында);
- 87,5% 64 кбит/сек жылдамдықпен РСМ телефониядан 8 кбит/сек жылдамдықпен ITU G.725 бойынша ақпарат тасымалдауға өткен кезде;
- 90% стереофонды аудио компакт дискілердің ақпараттарын 2 ∙ 16 бит ∙ 44 кГц = 1408 кбит/сек жылдамдықпен 112 кбит/сек жылдамдықты MPEG (Advanced Audio Coding) қысу стандартын қолданатын әдіспен және дерліктей бірмәнді сөйлем сапасымен кодтау кезінде.
Келесі мысал неміс әдеби мәтінінің энтропиясы болып табылады. Жиілік талдаудың нәтижелері 6.1 суретте көрсетілген. Егер әріптерді бөлектеп қарайтын болсақ, шамамен 4,7 бит/әріп-ке тең энтропияны аламыз. Әріптерді блоктарға біріктіріп, біз буын, сөз және т.б. секілді айқын байланыстарды қолданамыз, сол себепті өте үлкен ұзындықты блоктар үшін асимптотикалық жетімді шек 1,6 бит/әріп-ке тең.
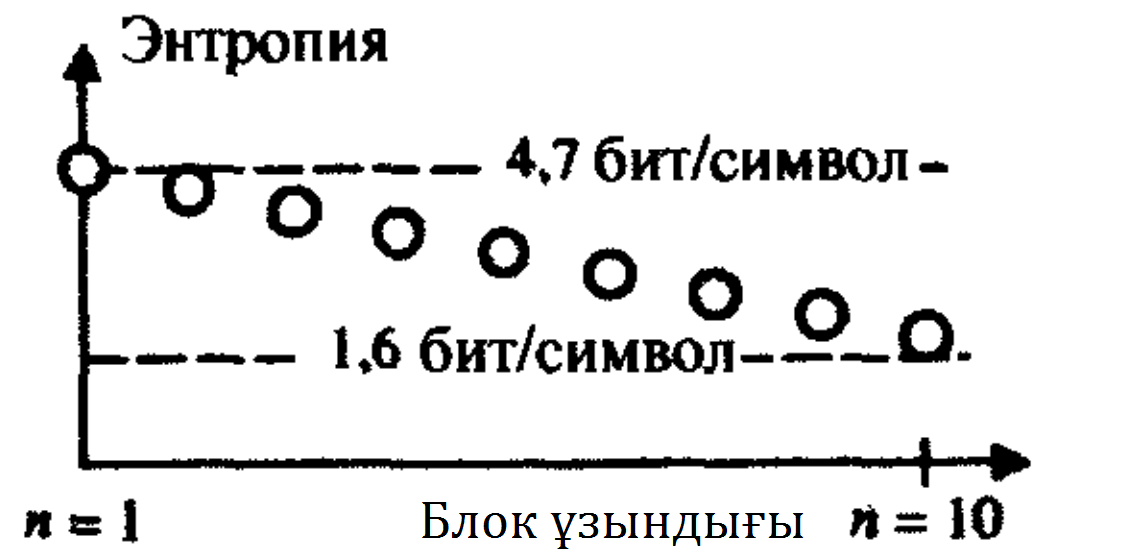
6.1 Сурет. Неміс әдеби тілінің блок ұзындығының функциясы
ретіндегі энтропиясы.
Мағлұматтарды қысу алгоритмін үш бөлікке бөлуге болады:
1. Статикалық алгоритмдер, мысалы, Хаффман кодтауы. Неміс әдеби мәтінін Хаффман әдісімен қысу ASCII стандартты ерікті символдарынан тұратын ақпаратты қысумен салыстырғанда, шамамен 50% ұтысқа жетуге мүмкіндік береді.
2. Адаптивті алгоритмдер, мысалы, түрлендірілген Хаффман кодтауы. Мұнда символдардың бөліну ықтималдықтары бастапқыда бірқалыпты болады, ал кейін статистиканың жинақталуына байланысты уақытта өзгереді.
3. Динамикалық алгоритмдер, мысалы ITU V42. bis ұсынысында қолданылатын кодтау.
Энтропиялық кодтаудың негізгі мәселесі символдар ықтималдық-тарының бөлінуін білуді болжау болып табылады. Көп жағдайда символдар статистикасы алдын-ала беймағлұм және эффективті кодтаудан алдын жиілік талдауы болуы қажет. Бұл жерде бізге көмекке универсалды алгоритмдер келеді.
● Адаптивті болып табылатын универсалды қысу алгоритмдері априоролық статистиканы қажет етпейді. Мұндай эффективті кодтау кодер кірісіне ақпарат келуімен дереу басталады.
● Мұнан басқа, дерліктей жеңіл техникалық күрделікті «жылдам» алгоритмдер бар.
● Шамаланған алгоритмдердің әрбірі қысудың жоғары дәрежесіне жетуге көмектеседі.
Қысу әдістерінің мысалы ретінде, екі маңызды алгоритмді қарап шығайық: жүйе барысында динамыкалық жиілік талдау жүретін арифметикалық кодтау және Лемпель-Зивтің универсалды алгоритмі. Лемпель-Зивтің LZ77 алгоритмі 1977 жылы ұсынылған болатын және 1984 жылы түрлендірді. Ол ITU V.42.bis ұсынысында қолданылады және LZW алгоритмі деп аталады.
