Уравнение медианы АМ и длину медианы АМ

ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ

Вариант №5

Выполнил:

студент факультета математики и

информационных технологий

Жарков О.С.

Донецк 2013

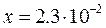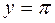Задание № 1Занести в некоторую переменную значения выражений при заданных и , отобразить результат.

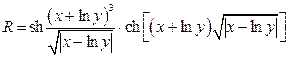
Решение

>> x=2.3*10^(-2)

x =0.0230

>> y=pi

y =3.1416

>> r=sinh((x+log(y))^3/sqrt(abs(x-log(y))))*cosh((x+log(y))*sqrt(abs(x-log(y))))

r = 3.9913

Задание № 2Необходимо ввести три матрицы А, В, С, состоящие из элементов случайным образом, распределенными из интервала (0,1) и выполнить необходимые действия. Известен размер матриц: А(3,3); В(4,3); С(3,4). Для каждой из матриц вычислить ее определитель.

(BCB–4C^T)A⁴

Решение

>> a=rand(3,3)

a =

0.0462 0.6948 0.0344

0.0971 0.3171 0.4387

0.8235 0.9502 0.3816

>> b=rand(4,3)

b =

0.7655 0.4456 0.2760

0.7952 0.6463 0.6797

0.1869 0.7094 0.6551

0.4898 0.7547 0.1626

>> c=rand(3,4)

c =

0.1190 0.3404 0.7513 0.6991

0.4984 0.5853 0.2551 0.8909

0.9597 0.2238 0.5060 0.9593

>> d=(b*c*b-4*c')*a^4

d =

-1.6634 -3.2211 -1.7993

1.3949 2.8650 1.5856

-0.2301 -0.4798 -0.2121

-3.0224 -6.1127 -3.4038

Считаем определитель для матрицы а:

>> A=det(a)

A =

0.2058

Определитель для матриц b и c мы не можем посчитать т.к. они не являются квадратными.

Задание № 3При помощи встроенных функций для заполнения стандартных матриц, двоеточием, индексацией и, возможно транспонированием или вычеркиванием получите следующие матрицы. Начальная матрица – нулевая.

Решение

>> a=zeros(7)

a =

0 0 0 0 0 0 0

0 0 0 0 0 0 0

0 0 0 0 0 0 0

0 0 0 0 0 0 0

0 0 0 0 0 0 0

0 0 0 0 0 0 0

0 0 0 0 0 0 0

>> a=a+diag(7*ones(6,1),1)

a =

0 7 0 0 0 0 0

0 0 7 0 0 0 0

0 0 0 7 0 0 0

0 0 0 0 7 0 0

0 0 0 0 0 7 0

0 0 0 0 0 0 7

0 0 0 0 0 0 0

>> a=a+diag(7*ones(6,1),-1)

a =

0 7 0 0 0 0 0

7 0 7 0 0 0 0

0 7 0 7 0 0 0

0 0 7 0 7 0 0

0 0 0 7 0 7 0

0 0 0 0 7 0 7

0 0 0 0 0 7 0

>> a=fliplr(a)

a =

0 0 0 0 0 7 0

0 0 0 0 7 0 7

0 0 0 7 0 7 0

0 0 7 0 7 0 0

0 7 0 7 0 0 0

7 0 7 0 0 0 0

0 7 0 0 0 0 0

>> a(1,:)=1:7

a =

1 2 3 4 5 6 7

0 0 0 0 7 0 7

0 0 0 7 0 7 0

0 0 7 0 7 0 0

0 7 0 7 0 0 0

7 0 7 0 0 0 0

0 7 0 0 0 0 0

>> a(:,1)=1:7

a =

1 2 3 4 5 6 7

2 0 0 0 7 0 7

3 0 0 7 0 7 0

4 0 7 0 7 0 0

5 7 0 7 0 0 0

6 0 7 0 0 0 0

7 7 0 0 0 0 0

>> a(7,:)=1:7

a =

1 2 3 4 5 6 7

2 0 0 0 7 0 7

3 0 0 7 0 7 0

4 0 7 0 7 0 0

5 7 0 7 0 0 0

6 0 7 0 0 0 0

1 2 3 4 5 6 7

>> a(:,7)=1

a =

1 2 3 4 5 6 1

2 0 0 0 7 0 1

3 0 0 7 0 7 1

4 0 7 0 7 0 1

5 7 0 7 0 0 1

6 0 7 0 0 0 1

1 2 3 4 5 6 1

Задание № 4:Вычислить пределы:

1)

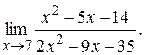
>> syms x

>> limit((x^2-5*x-14)/(2*x^2 -9*x-35),7)

ans = 9/19

2)

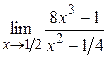
>> syms x

>> limit((8*x^3-1)/(x^2 -1/4),1/2)

ans = 6

3)

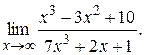
>> syms x

>> limit((x^3-3*x^2+10)/(7*x^3 +2*x+1),inf)

ans = 1/7

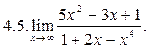
>> syms x

>> limit((5*x^2-3*x+1)/(x^4 +2*x+1),inf)

ans = 0

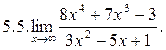
>> syms x

>> limit((8*x^4+7*x^3-3)/(3*x^2-5*x+1),inf)

ans = Inf

6)

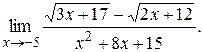
>> syms x

>> limit((sqrt(3*x+17)-sqrt(2*x+12))/(x^2+8*x+15),-5)

ans = 0.707

7)

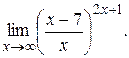
>> syms x

>> limit(((x-7)/x)^(2*x+1),inf)

ans = 1/exp(1)^14

8)

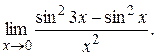
>> syms x

>> limit((sin(3*x)^2-sin(x)^2)/x^2,0)

ans = 8

Задание № 5:Даны векторы .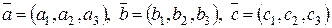

Определить:

1) длину вектора : ;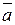

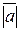2) скалярное произведение ;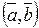

3) косинус угла между векторам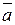и и ;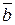

4) векторное произведение ; ;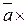

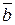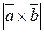5) смешанное произведение векторов , , ;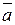

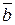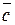6) выяснить коллинеарность векторов 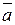і ;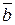

7) выяснить компланарность векторов , , .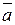

,

,

.

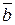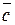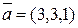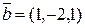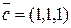Решение

>> a=[3 3 1]

a = 3 3 1

>> b=[1 -2 1]

b = 1 -2 1

>> c=[1 1 1]

c = 1 1 1

Длина векторов:

>> dl_a=sqrt( a(1)^2 + a(2)^2 +a(3)^2 )

dl_a =4.3589

>> dl_b=sqrt( b(1)^2 + b(2)^2 +b(3)^2 )

dl_b = 2.4495

Скалярное произведение:

>> sk_ab=dot(a,b)

sk_ab = -2

Косинус угла между векторами:

>> cos_ab=sk_ab/(dl_a*dl_b)

cos_ab = -0.1873

Векторное произведение:

>> vek_ab=cross(a,b)

vek_ab = 5 -2 -9

Смешаное произведение векторов:

>> smesh_abc=dot(cross(a, b), c)

smesh_abc = -6

Два вектора коллинеарные, если их векторное произведение равно нулю.

Для того чтобы два ненулевых вектора были коллинеарны, необходимо и достаточно, чтобы их координаты были пропорциональны

>> ab1=a(1)/b(1)

ab1 = 3

>> ab2=a(2)/b(2)

ab2 = -1.5000

>> ab3=a(3)/b(3)

ab3 = 1

Так как ab1 не равен ab2 не равен ab3, то вектора неколлинеарны.

Компланарность векторов:

Три вектора компланарны если их смешанное произведение равно нулю.

>> Komp=[a(1) a(2) a(3);b(1) b(2) b(3);c(1) c(2) c(3)]

Komp =

3 3 1

1 -2 1

1 1 1

>> Kom=det(Komp)

Kom = -6.0000

Так как определитель составленный из соответствующих векторов не равен нулю, значит вектора не компланарны.

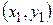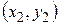Задание № 6:Даны вершины треугольника АВС: А , В , С 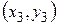. Найти:

1. Уравнение сторон АВ, АС.

2. Уравнение высоты СН.

3. Уравнение медианы АМ и длину медианы АМ.

4. Угол ВАС.

5. Уравнение прямой, которая проходит через вершину С, параллельно стороне АВ.

6. Точку пересечения медианы АМ и высоты СН.

7. Площадь треугольника АВС.

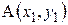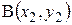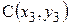	(-3, 2)	(2, 5)	(-1, -2)

Решение

Уравнение сторон АВ, АС.

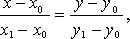
>> syms xh

>> syms yh

>> syms xp

>> syms yp

>> A=[-3;2]

A =

-3

>> B=[2;5]

B =

>> C=[-1;-2]

C =

-1

-2

Уравнение сторон АВ, АС.

text='uravnenie ax+by+c=0, dlya AB:'

text =uravnenie ax+by+c=0, dlya AB:

>> a1=B(2)-A(2)

a1 = 3

>> b1=A(1)-B(1)

b1 = -5

>> c1=A(2)*B(1)-A(1)*B(2)

c1 = 19

>> text='uravnenie ax+by+c=0, dlya AC:'

text =uravnenie ax+by+c=0, dlya AC:

>> a2=C(2)-A(2)

a2 = -4

>> b2=A(1)-C(1)

b2 = -2

>> c2=A(2)*C(1)-A(1)*C(2)

c2 = -8

Уравнение высоты СН.

Метод Крамера

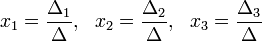
>> vectAB=[B(1)-A(1), B(2)-A(2)]

vectAB = 5 3

>> vectCH=[ xh - C(1) ; yh - C(2) ]

vectCH = xh + 1

yh + 2

>> 'koordinati tochki Н'

ans =koordinati tochki Н

>> M1=[B(1)-A(1), B(2)-A(2); a1, b1]

M1 =

5 3

3 -5

>> M2=[(B(1)-A(1))*C(1) + (B(2)-A(2))*C(2), B(2)-A(2); -c1, b1]

M2 =

-11 3

-19 -5

>> M3=[B(1)-A(1), (B(1)-A(1))*C(1) + (B(2)-A(2))*C(2); a1, -c1]

M3 =

5 -11

3 -19

>> xh=det(M2)/det(M1)

xh = -3.2941

>> yh=det(M3)/det(M1)

yh = 1.8235

>> text='uravnenie ax+by+c=0, dlya CH:'

text =uravnenie ax+by+c=0, dlya CH:

>> a3=yh-C(2)

a3 = 3.8235

>> b3=C(1)-xh

b3 = 2.2941

>> c3=C(2)*xh-C(1)*yh

c3 = 8.4118

Уравнение медианы АМ и длину медианы АМ

>> 'koordinati tochki M'

ans =koordinati tochki M

>> xm=(B(1)+C(1))/2

xm = 0.5000

>> ym=(B(2)+C(2))/2

ym = 1.5000

>> text='uravnenie ax+by+c=0, dlya AM:'

text =uravnenie ax+by+c=0, dlya AM:

>> a4=ym-A(2)

a4 = -0.5000

>> b4=A(1)-xm

b4 = -3.5000

>> c4=A(2)*xm-A(1)*ym

c4 = 5.5000

>> text='dlina AM:'

text =dlina AM:

>> dl=sqrt((A(1)-xm)^2 + (A(2)-ym)^2)

dl = 3.5355

Угол ВАС.

В общем случае, для нахождения углов в произвольном треугольнике можно воспользоваться теоремой косинусов
cos∠α = (b² + c² - a²) / 2 • b • c

text='dlini storon AB,AC,BC:'

text =dlini storon AB,AC,BC:

>> AB=sqrt((B(1)-A(1))^2 + (B(2)-A(2))^2)

AB = 5.8310

>> AC=sqrt((C(1)-A(1))^2 + (C(2)-A(2))^2)

AC = 4.4721

>> BC=sqrt((C(1)-B(1))^2 + (C(2)-B(2))^2)

BC = 7.6158

>> cosBAC=(AB^2 + AC^2 - BC^2) / (2*AB*AC)

cosBAC = -0.0767

>> ugolBAC=acos(cosBAC)

ugolBAC = 1.6476