Основные методы интегрирования
Теоретическая часть.
Первообразная функция.
Определение: Функция F(x) называется первообразной функциейфункции f(x) на отрезке [a, b], если в любой точке этого отрезка верно равенство:
F¢(x) = f(x).
Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.
F1(x) = F2(x) + C.
Неопределенный интеграл.
Определение: Неопределенным интеграломфункции f(x) называется совокупность первообразных функций, которые определены соотношением:
F(x) + C.
Записывают: 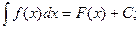
Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.
Свойства:
1. 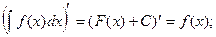
2. 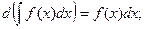
3. 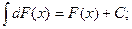
4. 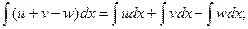 где u, v, w – некоторые функции от х.
где u, v, w – некоторые функции от х.
1. 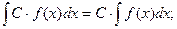
Таблица основных интегралов.
| Интеграл | Значение | Интеграл | Значение | ||
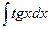 | -ln½cosx½+C | 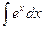 | ex + C | ||
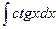 | ln½sinx½+ C | 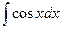 | sinx + C | ||
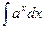 | 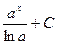 | 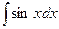 | -cosx + C | ||
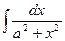 | 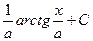 | 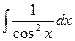 | tgx + C | ||
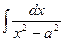 | 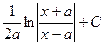 | 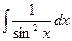 | -ctgx + C | ||
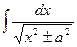 | ln 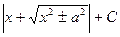 | 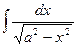 | arcsin 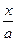 + C + C | ||
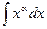 | 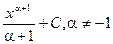 | 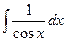 | 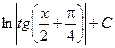 | ||
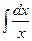 | 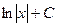 | 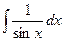 | 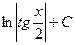 |
Основные методы интегрирования.
Способ подстановки (замены переменных).
Теорема: Если требуется найти интеграл 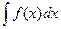 , но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
, но сложно отыскать первообразную, то с помощью замены x = j(t) и dx = j¢(t)dt получается:
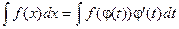
Доказательство: Продифференцируем предлагаемое равенство:
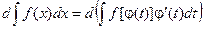
По рассмотренному выше свойству №2 неопределенного интеграла:
f(x)dx = f[j(t)]j¢(t)dt
что с учетом введенных обозначений и является исходным предположением. Теорема доказана.
Интегрирование по частям.
Способ основан на известной формуле производной произведения:
(uv)¢ = u¢v + v¢u
где u и v – некоторые функции от х.
В дифференциальной форме: d(uv) = udv + vdu
Проинтегрировав, получаем: 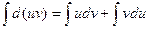 , а в соответствии с приведенными выше свойствами неопределенного интеграла:
, а в соответствии с приведенными выше свойствами неопределенного интеграла:
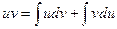 или
или 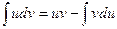 ;
;
Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.
Интегрирование элементарных дробей.
Определение: Элементарныминазываются дроби следующих четырех типов:
I. 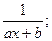 III.
III. 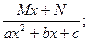
II. 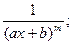 IV.
IV. 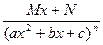
m, n – натуральные числа (m ³ 2, n ³ 2) и b2 – 4ac <0.
Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.
I. 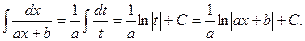
II. 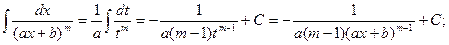
Рассмотрим метод интегрирования элементарных дробей вида III.
Интеграл дроби вида III может быть представлен в виде:
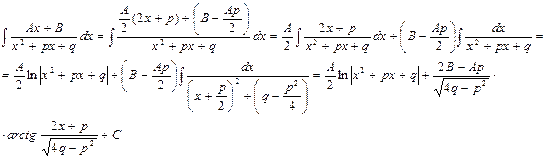
Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.
Рассмотрим теперь методы интегрирования простейших дробей IV типа.
Сначала рассмотрим частный случай при М = 0, N = 1.
Тогда интеграл вида 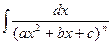 можно путем выделения в знаменателе полного квадрата представить в виде
можно путем выделения в знаменателе полного квадрата представить в виде 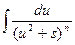 . Сделаем следующее преобразование:
. Сделаем следующее преобразование:
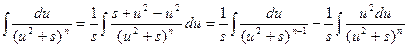 .
.
Второй интеграл, входящий в это равенство, будем брать по частям.
Обозначим: 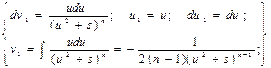
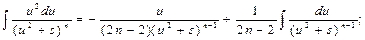
Для исходного интеграла получаем:
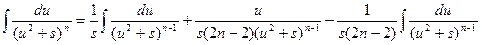
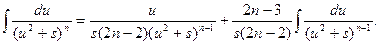
Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл 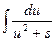 .
.
Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.
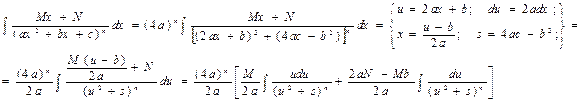
В полученном равенстве первый интеграл с помощью подстановки t = u2 + s приводится к табличному 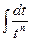 , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
, а ко второму интегралу применяется рассмотренная выше рекуррентная формула.
Интегрирование рациональных функций.
Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.
Теорема: Если 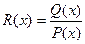 - правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x - a)a…(x - b)b(x2 + px + q)l…(x2 + rx + s)m ), то эта дробь может быть разложена на элементарные по следующей схеме:
- правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P(x) = (x - a)a…(x - b)b(x2 + px + q)l…(x2 + rx + s)m ), то эта дробь может быть разложена на элементарные по следующей схеме:
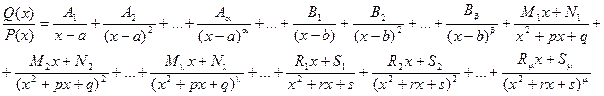
где Ai, Bi, Mi, Ni, Ri, Si – некоторые постоянные величины.
При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин Ai, Bi, Mi, Ni, Ri, Si применяют так называемый метод неопределенных коэффициентов, суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.
Интегрирование некоторых тригонометрических функций.
Интеграл вида 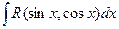 .
.
Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.
Интегралы этого вида вычисляются с помощью подстановки 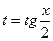 . Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.
. Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.
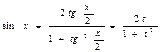 ,
, 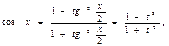
Тогда 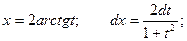
Таким образом: 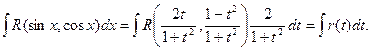
Описанное выше преобразование называется универсальной тригонометрической подстановкой.
Интеграл вида 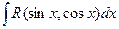 если
если
функция R является нечетной относительно cosx.
Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx.
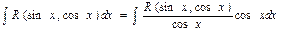
Функция 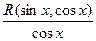 может содержать cosx только в четных степенях, а следовательно, может быть преобразована в рациональную функцию относительно sinx.
может содержать cosx только в четных степенях, а следовательно, может быть преобразована в рациональную функцию относительно sinx.
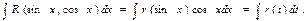
Интеграл вида 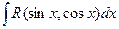
функция R четная относительно sinx и cosx.
Для преобразования функции R в рациональную используется подстановка
t = tgx.
Тогда 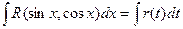
Интеграл произведения синусов и косинусов
различных аргументов.
В зависимости от типа произведения применятся одна из трех формул:
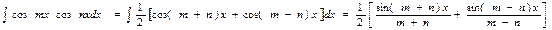
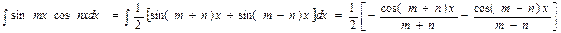
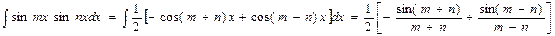
Интегрирование некоторых иррациональных функций.
Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.
Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.
Интеграл вида 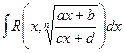 где n- натуральное число.
где n- натуральное число.
С помощью подстановки 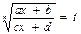 функция рационализируется.
функция рационализируется.