Обработка результатов измерений. 1. Используя полученные результаты, определите среднее угловые ускорения для каждой серии экспериментов.

1. Используя полученные результаты, определите среднее угловые ускорения для каждой серии экспериментов.

2. Определите момент инерции J_c по формуле (12).

3. Используя правила оценки погрешностей косвенных измерений, определите погрешности оценки момент инерции J_c.

4. Запишите окончательный результат работы в виде

J_c=(<J_c>±ΔJ_c)кг*м², δJ_c=... %,

где вместо <J_c> и ΔJ_c следует подставить полученные Вами численные значения этих величин, aδJ_с указывает относительную погрешность измерений.

Указания по технике безопасности

1. Перед выполнением работы получите инструктаж у лаборанта.

2. Соблюдайте общие правила техники безопасности работы в лаборатории "Физика".

3. Шнур наматывать на шкив виток к витку, вращая крестовину против часовой стрелки до перемещения груза 3 (рис.1) в верхнее положение.

Контрольные вопросы

1. Сформулируйте основной закон динамики вращательного движения.

2. Что называется моментом инерции твердого тела?

3. Что называется моментом силы, и в каких единицах он измеряется?

4. Сформулируйте и докажите теорему Штейнера.

6. Рассчитайте момент инерции тела по указанию преподавателя.

Лабораторная работа № 6

Колебания пружинного маятника

Цель лабораторной работы

Целью лабораторной работы является экспериментальное изучение колебаний пружинного маятника и ознакомление с методами определения параметров механических колебаний.

Задачи лабораторной работы

Задачей лабораторной работы является измерение зависимости периода колебаний от жесткости пружин и массы грузов.

Экспериментальное

Оборудование, приборы и

Принадлежности

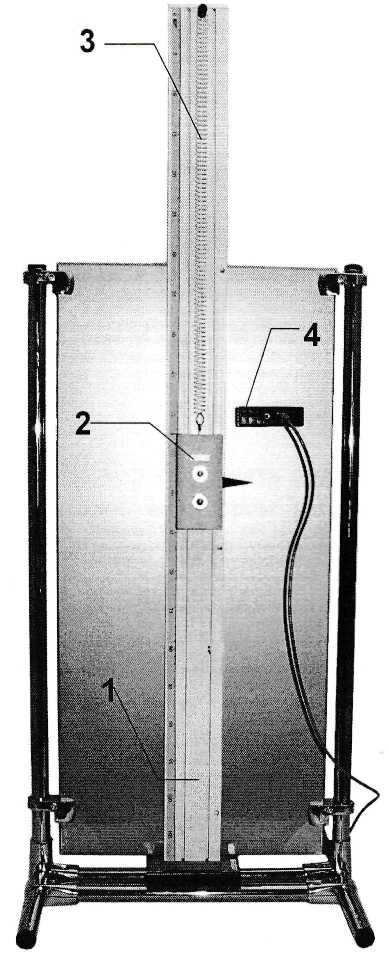
Лабораторный стенд (рис.1) включает в себя вертикальную опорную конструкцию с направляющими пазами 1, а также набор пружин и подвижную каретку 2, в отверстии которой может фиксироваться дополнительный груз (рис.2).

К приборам и принадлежностям относятся оптический датчик 4, компьютер с необходимым

Программным обеспечением,

концентратор для подключения датчика к компьютеру.

Рис. 1

Теоретическая часть

В линейных упругих системах действует закон Гука: 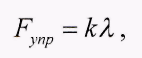(1)

где F_упр-величина упругой силы, например, пружины, измеряемая в ньютонах, k- коэффициент жесткости пружины (Н/м),

λ-растяжение/сжатие пружины (м) из положения своего недеформированного состояния.

Рассмотрим силы, действующие на пружинный маятник, расположенный вертикально (силами сопротивления движению пренебрежем). Это: сила тяжести mg и сила упругого подвеса F_ynp, стремящаяся вернуть пружину в исходное, нерастянутое положение.

Второй закон Ньютона для этого случая можно написать так:

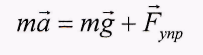(2)

Если отсчитывать смещение тела х из своего положения статического равновесия, в котором растяжение пружины равно статическому λ_сm, то проекция этого уравнения на наклонную плоскость (ось х) будет:

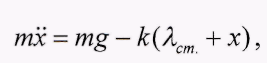(3)

где х-ускорение тела, определяемое как вторая производная по времени от смещения х, а величина λ_сm + х - полное растяжение пружины.

Условием равновесия тела массой m на пружине является равенство силы тяжести и статической упругой силы пружины mg = F_упр^ст.В свою

очередь, равновесная статическая упругая сила пружины определяется статическим смещением из положения равновесия λ_сm. Тогда:

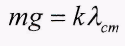(4)

С использованием (4) уравнение (3) приобретет вид: 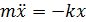что после нормировки (деления на m) позволяет его записать в виде:

(5)

Здесь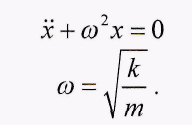

Выражение (5) - дифференциальное уравнение свободных колебаний. Решение дифференциального уравнения (5) представляет собой гармонические колебания вида:

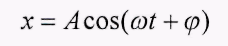(6)

Здесь А, φ- амплитуда и начальная фаза колебаний, а величина ω

носит название частоты собственных колебаний. По частоте колебаний определяют период колебаний Т:

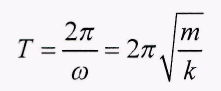(7)

Используя значение периода колебания, можно найти и жесткость пружины:

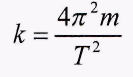(8)

В том случае, если использовать два различных груза m₁и m₂, то по соответствующим периодам собственных колебаний оценивают жесткость пружины (динамический метод):

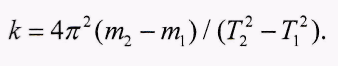(9)