Локальная и интегральная теорема Муавра-Лапласа

ЛЕКЦИИ

Определение вероятности события

Классическое определение вероятности события. При классическом определении вероятность события определяется равенством

P(A)=m/n,

где m – число элементарных исходов испытания, благоприятствующих появлению события A; n – число возможных элементарных исходов испытания. Предполагается, что элементарные исходы образуют полную группу и равновозможны.

Геометрическое определение вероятности. Пусть отрезок l составляет часть отрезка L. На отрезке L наудачу поставлена случайная точка. Если предположить, что вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L, то вероятность попадания точки на отрезок l определяется равенством

P = Длина l/Длина L

Теорема сложения вероятностей

Теорема сложения вероятностей несовместных событий. Вероятность появления одного из двух несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р(А + В) = Р(А) + Р(В).

Следствие. Вероятность появления одного из нескольких попарно несовместных событий, безразлично какого, равна сумме вероятностей этих событий:

Р(А₁+А₂+...+А_n) = P(A₁) + Р(А₂) +…+ Р(А_n).

Теорема сложения вероятностей совместных событий. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления

Р(А+В) = Р(А) + Р(В) – Р(АВ).

Теорема может быть обобщена на любое конечное число совместных событии. Например, для трех совместных событий

Р(A+В+С) = Р(А) + Р(В) + Р(С) – Р(АВ) – Р(АС) – Р(ВС) + Р(ABC).

Теорема умножения вероятностей

Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Р(АВ) = Р(А)∙Р_A(В).

В частности, для независимых событий

P(АВ) = Р(А)∙Р(В),

т. е. вероятность совместного появления двух независимых событий равна произведению вероятностей этих событий.

Формула полной вероятности

Вероятность события А, которое может наступить лишь при появлении одного из несовместных событий (гипотез) H₁, H₂, …, H_n образующих полную группу, равна сумме произведений вероятностей каждой из гипотез на соответствующую условную вероятность события A:

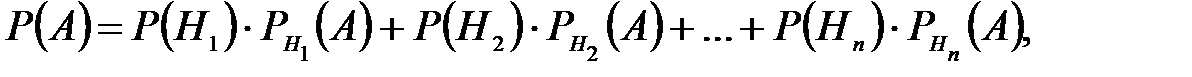
где .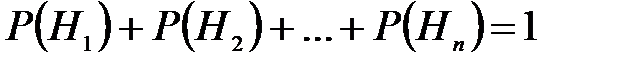

Формула Байеса

Пусть событие А может наступить лишь при условии появления одного из несовместных событий (гипотез) H₁, H₂, …,H_n, которые образуют полную группу событий. Если событие А уже произошло, то вероятности гипотез могут быть переоценены по формулам Байеса

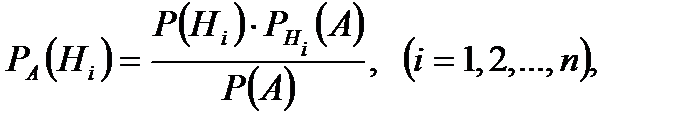
где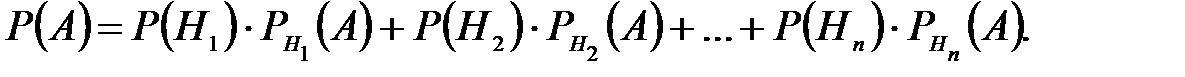

Формула Бернулли

Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна p (0 < p < 1), событие наступит ровно m раз (безразлично, в какой последовательности), равна

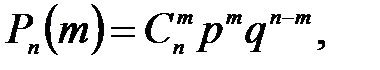где 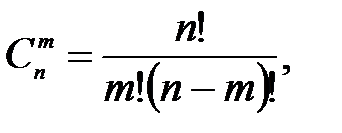q = 1 – p.

Вероятность того, что в n испытаниях событие наступит: а) менее m раз; б) более m раз; в) не менее m раз; г) не более m раз, находят соответственно по формулам:

P_n(0) + P_n(1) +…+ P_n(m – 1);

P_n(m + 1) + P_n(m + 2) +…+ P_n(n);

P_n(m) + P_n(m + 1) +…+ P_n(n);

P_n(0) + P_n(1) +…+ P_n(m).

Формула Пуассона

Если вероятность p наступления события A – постоянна и мала, а число испытаний n – велико и число λ = np – незначительно (будем полагать, что λ = np ≤ 10), то имеет место приближенное равенство:

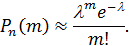
Локальная и интегральная теорема Муавра-Лапласа

Локальная теорема.Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р <1), событие наступит ровно m раз (безразлично, в какой последовательности), приближенно равна (тем точнее, чем больше n)

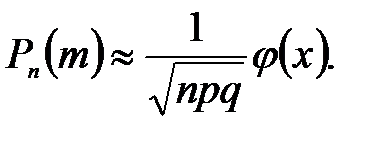
Здесь

, ,

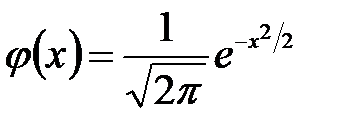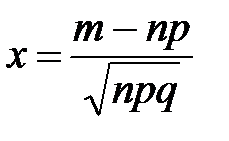Таблица значений функции Гаусса 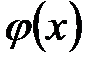для положительных значений х приведена в приложении 1; для отрицательных значений х пользуются этой же таблицей с учетом того, что функция 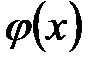четная, следовательно, .

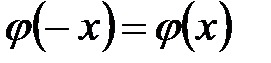Интегральная теорема.Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие наступит не менее m₁ раз и не более m₂ раз, приближенно равна

P(m₁; m₂) = Φ(x¢¢) – Φ(x¢)

Здесь 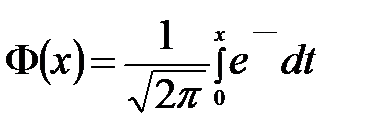– функция Лапласа,

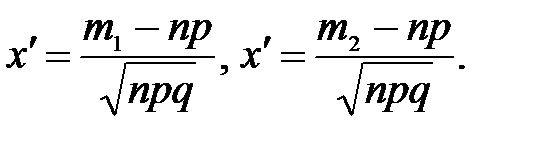
Таблица значений функции Лапласа для положительных значений х (0 ≤ х ≤ 5) приведена в приложении 2; для значений х > 5 полагают Φ(x) = 0,5. Для отрицательных значений х используют эту же таблицу, учитывая, что функция Лапласа нечетная Ф(–x)= –Ф(x).

На практике, приближенные равенства из локальной и интегральной теоремы Муавра-Лапласа используют при выполнении условия: npq > 20.