Применение теории делимости к решению неопределенных уравнений в целых числах
Определение. Неопределенные уравнения - уравнения, содержащие более одного неизвестного.
Под одним решением неопределенного уравнения понимается совокупность значений неизвестных, которая обращает данное уравнение в верное равенство.
Пример 1. Решить в целых числах уравнение 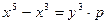 , где y и p - простые числа.
, где y и p - простые числа.
Решение
Преобразуем уравнение 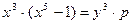 . Если имеются целые решения этого уравнения, тогда
. Если имеются целые решения этого уравнения, тогда 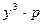 делится на
делится на 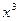 , так как НОД (x3, x2 - 1) = 1, но y3 и p являются взаимно простыми числами, т. е.
, так как НОД (x3, x2 - 1) = 1, но y3 и p являются взаимно простыми числами, т. е. 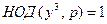 , значит, p не делится на x3, следовательно, y3 делится на x3, что возможно, если x = y, т. е. x - простое число. Тогда
, значит, p не делится на x3, следовательно, y3 делится на x3, что возможно, если x = y, т. е. x - простое число. Тогда 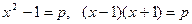 , что возможно, если
, что возможно, если 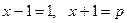 , т. е. x = 2, y = 2, p = 3.
, т. е. x = 2, y = 2, p = 3.
Ответ: x = 2, y = 2, p = 3.
Пример 2. Найти целые решения уравнения 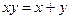 .
.
Решение
Преобразуем уравнение 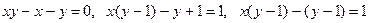 ,
,
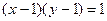 . Произведение целых чисел будет равно 1 в двух случаях, когда каждый из сомножителей равен 1, и когда каждый из сомножителей равен -1.
. Произведение целых чисел будет равно 1 в двух случаях, когда каждый из сомножителей равен 1, и когда каждый из сомножителей равен -1.
Получим совокупность двух систем уравнений:
(1) 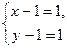 и (2)
и (2) 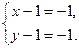
Решим каждую систему уравнений: (1) 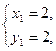 (2)
(2) 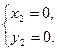
Ответ: 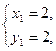
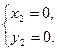
Пример 3. Найти все целые решения уравнения: 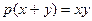 , где p - простое число.
, где p - простое число.
Решение
Преобразуем уравнение:
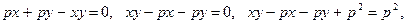
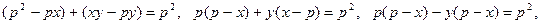
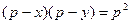 .
.
Произведение двух множителей равно целому числу 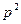 . Очевидно, что каждый из множителей должен быть числом целым, следовательно, получим системы уравнений, которые представляют всевозможные случаи, когда множители целые и их произведение равно
. Очевидно, что каждый из множителей должен быть числом целым, следовательно, получим системы уравнений, которые представляют всевозможные случаи, когда множители целые и их произведение равно 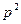 ,
,
(1) 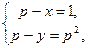 (2)
(2) 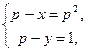 (3)
(3) 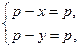 (4)
(4) 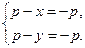
В результате решения систем, получаем:
(1) 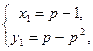 (2)
(2) 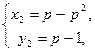 (3)
(3) 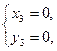 (4)
(4) 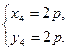
Ответ: 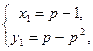
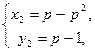
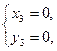
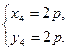
Пример 4. Найти все целые решения уравнения: 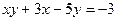 .
.
Решение
Преобразуем уравнение: 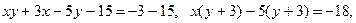
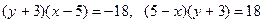 .
.
Произведение двух целых сомножителей равно 18. Чтобы выяснить, каким числам могут быть равны эти сомножители, найдем все делители числа 18:
18 имеет делители: 1, 2, 3, 6, 9, 18. Если первый множитель равен первому из делителей 18, тогда второй множитель будет равен последнему - получим шесть пар решений:
(1) 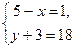 (2)
(2) 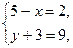 (3)
(3) 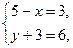
(4) 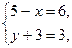 (5)
(5) 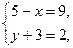 (6)
(6) 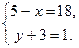
(1) 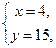 (2)
(2) 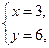 (3)
(3) 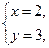 (4)
(4) 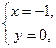 (5)
(5) 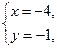 (6)
(6) 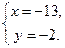
Ответ: 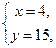
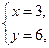
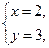
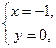
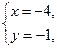
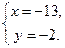
Пример 5. Найти натуральные значения корней уравнения
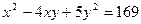 .
.
Решение
Преобразуем уравнение: 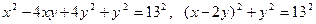 .
.
Отсюда получаем четыре системы уравнений:
(1) 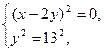 (2)
(2) 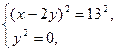 (3)
(3) 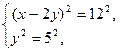 (4)
(4) 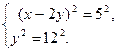
Поскольку x и y - натуральные числа, находим:
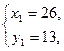
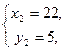
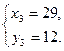
Ответ: 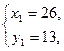
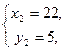
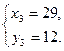
Уравнения вида ax + by = c, где a, b, c - целые числа, отличные от нуля
Теорема 1. Если НОД (a; b) = d, то существуют такие целые числа x и y, что имеет место равенство 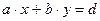 .
.
(Это равенство называется линейной комбинацией или линейным представлением наибольшего общего делителя двух чисел через сами эти числа.)
Пример. Найти линейное представление наибольшего общего делителя чисел 1232 и 1672.
Решение
1) Применим алгоритм Евклида и найдем НОД(1232, 1672):
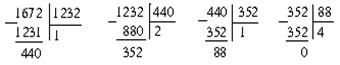
НОД(1232, 1672) = 88.
2) Выразим 88 последовательно через неполные частные и остатки, используя полученные равенства, начиная с конца:
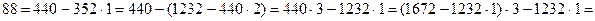
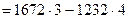 , т. е.
, т. е. 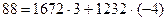 .
.
Теорема 2. Если в уравнении ax + by = l (a, b) = 1, то уравнение имеет по крайней мере одно целое решение.
Справедливость этой теоремы следует из теоремы 1. Таким образом, чтобы найти одно целое решение уравнения ах + by = 1, если (а, b) = 1, достаточно представить число 1 в виде линейной комбинации чисел а и b.
Пример. Найти целое решение уравнения 15x + 37y = 1.
Решение
1) Применим алгоритм Евклида и найдем НОД(15, 37):
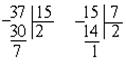
НОД(15, 37) = 1
2) Выразим 1 последовательно через неполные частные и остатки, используя полученные равенства, начиная с конца:
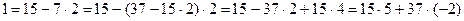 , т. е.
, т. е.
x0 = 5, y0 = -2.
Теорема 3. Если в уравнении ах + by = с (а, b) = d > 1 и с не делится на d, то уравнение целых решений не имеет.
Для доказательства теоремы достаточно предположить противное.
Пример. Найти целое решение уравнения 16x - 34y = 7.
Решение
(16, 34) = 2, 7 не делится на 2, уравнение целых решений не имеет.
Теорема 4. Если в уравнении ах + by = с (a, b) = d > 1 и c делится на d, то оно равносильно уравнению а1х + b1у = c1, в котором (a1, b1) = 1.
При доказательстве теоремы следует показать, что произвольное целое решение первого уравнения является также решением второго уравнения и обратно.
Теорема 5. Если в уравнении ах + by = с (а, b) = 1, то все целые решения этого уравнения заключены в формулах:
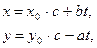
где x0, y0 - целое решение уравнения ах + by = 1, t - любое целое число.
При доказательстве теоремы следует показать, во-первых, что приведенные формулы действительно дают решения данного уравнения и, во-вторых, что произвольное целое решение этого уравнения заключено в приведенных формулах.
Приведенные теоремы позволяют установить следующее правило решения в целых числах уравнения ах + by = с, где (а, b) = 1:
1) находится целое решение уравнения ах + by = 1 путем представления 1 как линейной комбинации чисел а и b (существуют и другие способы отыскания целых решений этого уравнения, например при использовании цепных дробей);
2) составляется общая формула целых решений данного уравнения:
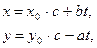
где x0, y0 - целое решение уравнения ах + by = 1, t—любое целое число.
Придавая t определенные целые значения, можно получить частные решения данного уравнения: наименьшие по абсолютной величине, наименьшие положительные (если можно) и т. д.
Пример 1. Найти целые решения уравнения 407х - 2816у = 33.
Решение
1) Упрощаем данное уравнение, приводя его к виду 37х - 256у = 3.
2) Решаем уравнение 37x - 256y = 1.
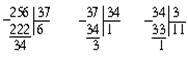
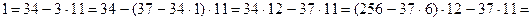
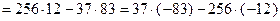 .
.
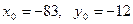 .
.
3) Найдем решения данного уравнения по формулам: 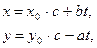
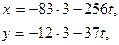
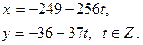
Ответ: 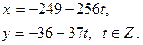
Пример 2. Найти наибольшее трехзначное число, которое при делении на 17 дает остаток 9, а при делении на 22 дает остаток 4.
Решение
Пусть частное от деления трехзначного числа на 17 равно x, тогда искомое число равно: 17x + 9, причем 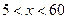 . Так как при
. Так как при 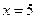 получаем двузначное число, а при x = 6 - уже трехзначное; при x = 60 получим четырехзначное число, а при x = 59 будет число трехзначное.
получаем двузначное число, а при x = 6 - уже трехзначное; при x = 60 получим четырехзначное число, а при x = 59 будет число трехзначное.
Пусть частное от деления трехзначного числа на 22 равно y, тогда искомое число равно: 22y + 4, причем 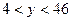 . Этот промежуток устанавливаем аналогично промежутку для значений x.
. Этот промежуток устанавливаем аналогично промежутку для значений x.
По условию: 17x + 9 = 22y + 4, 22y - 17x = 5 - это неопределенное уравнение.
1) Решим уравнение: -17x + 22y = 1.
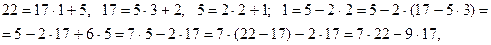
значит, 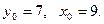
2) Общий вид всех целых решений данного уравнения:
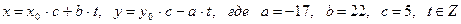 .
.
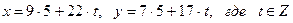 .
.
Положим 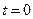 , тогда
, тогда 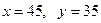 , если t = 1, тогда x = 67, y = 52 - эти значения уже выходят за пределы промежутков
, если t = 1, тогда x = 67, y = 52 - эти значения уже выходят за пределы промежутков 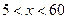 и
и 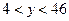 .
.
Поскольку требуется найти наибольшее трехзначное число, то удовлетворять условию задачи будут значения 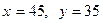 .
.
Искомое трехзначное число будет равно:
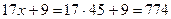 или
или 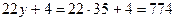 .
.
Ответ: 774.
[1] Примечание. Надо заметить, что эта теорема верна только тогда, когда делители - числа взаимно простые. Если же делители - числа не взаимно простые, то данное число хотя и будет делится порознь на каждый делитель, но на их произведение может и не делится.
Например, число 840 делится на 120, и на 140; на произведение же , очевидно, число 840 не разделится.
