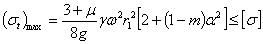Напряжения в сферических толстостенных сосудах.
На фиг. 547 изображен элемент, вырезанный из толщи стенки толстостенного сферического сосуда; внутренний радиус этого элемента равен r, а наружный 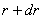 ; напряжения, действующие на этот элемент, изображены на чертеже.
; напряжения, действующие на этот элемент, изображены на чертеже.
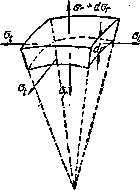
Рис.6. фрагмент сферического толстостенного сосуда.
Составляя уравнения равновесия и совместности, получаем для  и
и 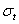 значения:
значения:
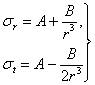
Постоянные А и В могут быть определены из условий на внутренней и внешней поверхностях сосуда при
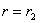 и
и 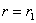
соответственно, где 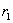 и
и 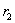 — наружный и внутренний радиусы.
— наружный и внутренний радиусы.
Так, при действии внешнего 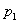 и внутреннего
и внутреннего 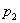 давлений А и В определяются из условий:
давлений А и В определяются из условий:
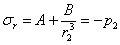 на внутренней поверхности,
на внутренней поверхности,
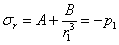 на внешней поверхности
на внешней поверхности
Отсюда
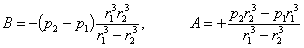
Тогда
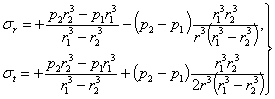
Лекция № 40. Расчет тонкостенных сосудов и резервуаров.
Если толщина стенок цилиндра 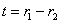 мала по сравнению с радиусами
мала по сравнению с радиусами 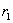 и
и 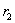 , то известное выражение для тангенцальных напряжений приобретает вид
, то известное выражение для тангенцальных напряжений приобретает вид
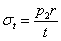
т. е. величину, определенную нами раньше (§ 34).
Для тонкостенных резервуаров, имеющих форму поверхностей вращения и находящихся под внутренним давлением р, распределенным симметрично относительно оси вращения, можно вывести общую формулу для вычисления напряжений.
Выделим (Рис.1) из рассматриваемого резервуара элемент двумя смежными меридиональными сечениями и двумя сечениями, нормальными к меридиану.

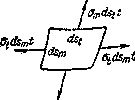
Рис.1. Фрагмент тонкостенного резервуара и его напряженное состояние.
Размеры элемента по меридиану и по перпендикулярному к нему направлению обозначим соответственно 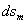 и
и 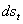 , радиусы кривизны меридиана и перпендикулярного к нему сечения обозначим
, радиусы кривизны меридиана и перпендикулярного к нему сечения обозначим 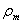 и
и 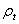 , толщину стенки назовем t.
, толщину стенки назовем t.
По симметрии по граням выделенного элемента будут действовать только нормальные напряжения 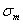 в меридиальном направления и
в меридиальном направления и 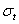 в направлении, перпендикулярном к меридиану. Соответствующие усилия, приложенные к граням элемента, будут
в направлении, перпендикулярном к меридиану. Соответствующие усилия, приложенные к граням элемента, будут 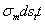 и
и 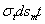 . Так как тонкая оболочка сопротивляется только растяжению, подобно гибкой нити, то эти усилия будут направлены по касательной к меридиану и к сечению, нормальному к меридиану.
. Так как тонкая оболочка сопротивляется только растяжению, подобно гибкой нити, то эти усилия будут направлены по касательной к меридиану и к сечению, нормальному к меридиану.
Усилия 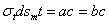 (Рис.2) дадут в нормальном к поверхности элемента направлении равнодействующую ab, равную
(Рис.2) дадут в нормальном к поверхности элемента направлении равнодействующую ab, равную
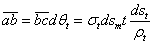
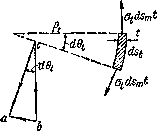
Рис.2. Равновесие элемента тонкостенного резервуара
Подобным же образом усилия 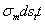 дадут в том же направлении равнодействующую
дадут в том же направлении равнодействующую 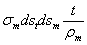 Сумма этих усилий уравновешивает нормальное давление, приложенное к элементу
Сумма этих усилий уравновешивает нормальное давление, приложенное к элементу
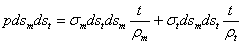
Отсюда
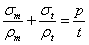
Это основное уравнение, связывающее напряжения 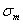 и
и 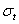 для тонкостенных сосудов вращения, дано Лапласом.
для тонкостенных сосудов вращения, дано Лапласом.
Так как мы задались распределением (равномерным) напряжений по толщине стенки, то задача статически определима; второе уравнение равновесия получится, если мы рассмотрим равновесие нижней, отрезанной каким-либо параллельным кругом, части резервуара.
Рассмотрим случай гидростатической нагрузки (рис.3). Меридиональную кривую отнесем к осям х и у с началом координат в вершине кривой. Сечение проведем на уровне у от точки О. Радиус соответствующего параллельного круга будет х.
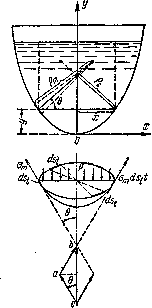
Рис.3. Равновесие нижнего фрагмента тонкостенного резервуара.
Каждая пара усилий 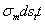 , действующих на диаметрально противоположные элементы
, действующих на диаметрально противоположные элементы 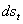 проведенного сечения, дает вертикальную равнодействующую bс, равную
проведенного сечения, дает вертикальную равнодействующую bс, равную
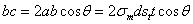
сумма этих усилий, действующих по всей окружности проведенного сечения, будет равна 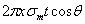 ; она будет уравновешивать давление жидкости
; она будет уравновешивать давление жидкости 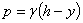 на этом уровне плюс вес жидкости в отрезанной части сосуда
на этом уровне плюс вес жидкости в отрезанной части сосуда 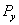 .
.
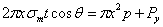
Отсюда
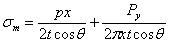
Зная уравнение меридиональной кривой, можно найти 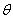 , х и
, х и 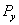 для каждого значения у, и стало быть, найти
для каждого значения у, и стало быть, найти 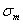 , а из уравнения Лапласа и
, а из уравнения Лапласа и 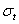
Например, для конического резервуара с углом при вершине 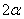 , наполненного жидкостью с объемным весом у на высоту h, будем иметь:
, наполненного жидкостью с объемным весом у на высоту h, будем иметь:
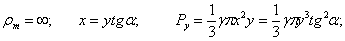
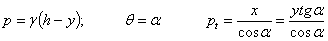
тогда
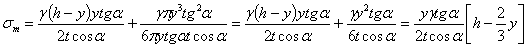
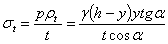
Для сферического сосуда радиусом 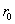 , находящегося под внутренним давлением
, находящегося под внутренним давлением 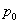 , по симметрии
, по симметрии 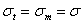 ; тогда из уравнения (Лапласа), так как
; тогда из уравнения (Лапласа), так как
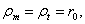
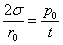 и
и 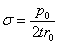
Если меридиональная кривая будет иметь переломы с разрывом непрерывности угла 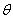 , то равновесие тонкой оболочки у места перелома может быть обеспечено лишь наличием реакций, приложенных к оболочке по окружности в этом месте. Появление таких реакций обеспечивается устройством специальных колец, способных брать на себя усилия, возникающие в них в связи с неуравновешенностью напряжений
, то равновесие тонкой оболочки у места перелома может быть обеспечено лишь наличием реакций, приложенных к оболочке по окружности в этом месте. Появление таких реакций обеспечивается устройством специальных колец, способных брать на себя усилия, возникающие в них в связи с неуравновешенностью напряжений 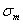 по обе стороны точки перелома.
по обе стороны точки перелома.
Лекция № 41. Расчет быстровращающегося диска
Значительный интерес представляет задача о напряжениях и деформациях в быстро вращающихся валах и дисках. Высокие скорости вращения валов паровых турбин обусловливают появление в валах и дисках значительных центробежных усилий. Вызванные ими напряжения распределяются симметрично относительно оси вращения диска.
Рассмотрим наиболее простую задачу о расчете диска постоянной толщины. Расчет такого диска положен в основу некоторых приближенных способов расчета дисков любого профиля. Воспользуемся некоторыми результатами, полученными при выводе формул для расчета толстостенных цилиндров. Предположим, что по толщине диска, принимаемой равной единице, напряжения  и
и 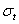 не меняются; осевое напряжение
не меняются; осевое напряжение 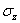 будем считать равным нулю.
будем считать равным нулю.
Составим условия равновесия элемента АВ, выделенного из диска двумя меридиональными сечениями и двумя концентрическими цилиндрическими поверхностями (фиг. 586). В данном случае, кроме сил, действующих по граням элемента АВ, необходимо принять во внимание также и силу инерции
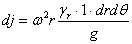
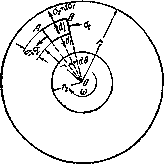
Рис.1. Расчетная схема вращающегося диска.
направленную вдоль радиуса от центра к внешнему контуру диска. Вместо ранее полученного уравнения равновесия получим:
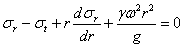 | (1) |
Уравнение условий совместности деформаций также остаются в силе и для данной задачи, т. е.
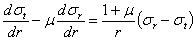 | (1) |
Подставляя в это уравнение значение разности 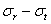 из (35.4), находим:
из (35.4), находим:
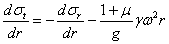 | (2) |
Дифференцируя уравнение (1) по r и подставляя в него вместо 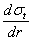 его значение из формулы (2), получаем линейное дифференциальное уравнение
его значение из формулы (2), получаем линейное дифференциальное уравнение
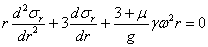
или
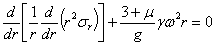
Интегрируя это уравнение, находим:
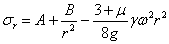 | (4) |
Из (1) и (4) следует, что
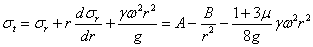 | (5) |
В формулах (4) и (5) А и В — постоянные интегрирования, которые должны быть определены из условий на контуре диска. При определении постоянных рассмотрим два случая: 1) диск с отверстием в центре и 2) сплошной диск. При этом вначале предположим, что края диска свободны от внешних усилий.
Для диска с центральным отверстием напряжение  должно быть равно нулю как при
должно быть равно нулю как при 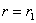 , так и при
, так и при 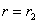 (рис.1). Эти условия на контуре при подстановке их в формулу (4) приводят к уравнениям:
(рис.1). Эти условия на контуре при подстановке их в формулу (4) приводят к уравнениям:
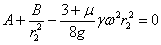
и
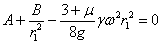
откуда
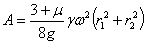 и
и 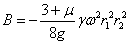
Подставляя значения А и В в формулы (35.7) и (35.8), получаем:
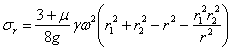
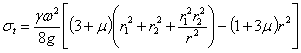
Полагая для краткости можем написать:
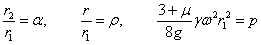 и
и 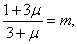
можем написать:
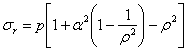
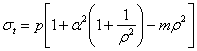
Замечаем, что напряжение  обращается в нуль при
обращается в нуль при 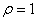 и
и 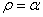 , т. е. на внутреннем и наружном контурах диска; при значениях
, т. е. на внутреннем и наружном контурах диска; при значениях 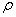 между 1 и
между 1 и 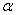 напряжение
напряжение  положительно и, как нетрудно убедиться, достигает наибольшей величины при
положительно и, как нетрудно убедиться, достигает наибольшей величины при 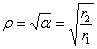 При этом
При этом
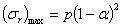 | (6) |
Напряжение 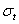 при всех значениях
при всех значениях 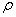 также положительно и наибольшей величины достигает у внутреннего края диска, где
также положительно и наибольшей величины достигает у внутреннего края диска, где 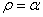 :
:
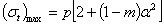 | (7) |
Сравнивая выражения (6) и (7), убеждаемся, что 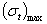 всегда больше
всегда больше 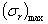 Поэтому при проверке прочности диска как по теории наибольших касательных напряжений, так и по энергетической теории условие прочности должно быть написано в таком виде:
Поэтому при проверке прочности диска как по теории наибольших касательных напряжений, так и по энергетической теории условие прочности должно быть написано в таком виде: