Проверка предпосылок проведения регрессионного анализа

Основные понятия классического регрессионного анализа

В пассивном эксперименте исходная информация о функционировании сложной системы может быть получена путем непрерывной или дискретной фиксации уровней исследуемых входных факторов и выходных параметров системы в условиях ее нормального функционирования. В данном случае, как уровни, так и сочетания уровней всех входных факторов в каждый момент времени будут являться случайными величинами. Случайными величинами будут являться и выходные параметры системы. При проведении пассивного эксперимента исследователь каждому сочетанию уровней всех входных факторов должен поставить в соответствие текущий уровень выходных параметров системы. Полученная таким образом информация может быть представлена в виде следующей таблицы

Таблица 1.1 – Результаты пассивного эксперимента

Опыты	Входные параметры	Выходные параметры
	…		…			…		…
		…		…			…
		…		…			…
…	…	…	…	…	…	…	…	…	…	…
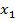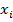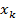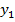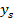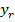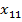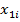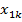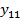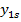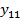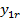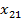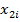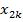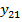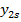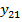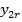j		…		…			…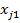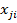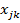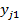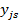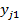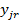
…	…	…	…	…	…	…	…	…	…	…
N		…		…			…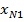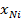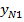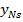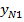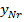

Входные параметры системы 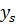стохастически связаны с входными параметрами 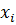. В общем виде эту связь можно представить выражением:

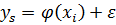(1.1)

где 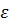- аддитивная помеха, то есть величина, учитывающая случайные ошибки измерений, случайные шумы, влияние неучтенных факторов.

Данную аналитическую зависимость принято называть математической моделью системы, полученной по результатам пассивного эксперимента.

Так как уровни входных факторов, полученных при испытаниях, как правило, имеют различный порядок, то для упрощения вычислений все ячейки таблицы 1.1 необходимо отцентрировать и, кроме того, целесообразно добавить первый столбец ( 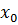- фиктивный столбец), состоящий из единиц. Тогда таблица результатов эксперимента примет окончательный вид (таблица 1.2).

Таблица 1.2 – Результаты пассивного эксперимента

Опыты		Входные параметры	Выходные параметры
		…		…			…		…
			…		…			…
			…		…			…
…	…	…	…	…	…	…	…	…	…	…	…
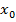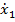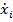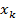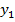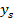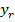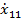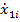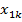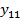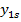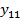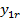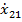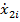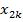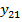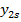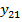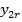j			…		…			…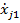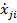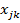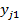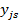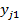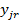
…	…	…	…	…	…	…	…	…	…	…	…
N			…		…			…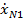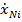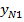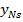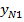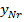

В таблице 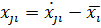1.2

(1.2)

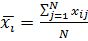
Очевидно, что ошибка в j-м опыте, которая будет характеризировать точность подбираемой модели системы, может быть записана в виде:

,

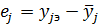где

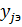- величина выходного параметра системы, полученная по результатам эксперимента в ;

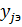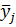- величина выходного параметра системы, рассчитанная для j-го опыта по подобранной математической модели.

Целесообразно так подобрать математическую модель, чтобы по всем опытам выполнялось условие:

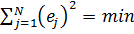(3)

Так как подбираемая по результатам эксперимента математическая модель системы, как правило, по своему виду не имеет ничего общего с природой процессов, происходящих в системе, то в качестве функции 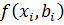целесообразно выбирать простые аналитические зависимости.

В инженерной практике наиболее распространены три вида уравнений регрессии:

- линейное

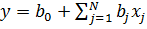(4)

- неполноквадратичное

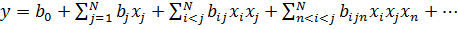(5)

- полноквадратичное

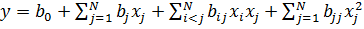(6)

где любой коэффициент уравнения регрессии 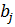определяется как

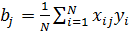(7)

После расчета коэффициентов 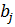полученное уравнение приближенной регрессии подвергается статистическому анализу.

При этом оценивают ошибку от замены истинной регрессии приближенной и проверяют значимость всех слагаемых найденного уравнения в сравнении со случайной ошибкой наблюдений. Данный комплекс мероприятий носит название «регрессионного анализа».

Проведение регрессионного анализа возможно только при выполнении следующих предпосылок.

1) Ошибка измерения входных факторов 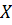равна нулю. Данное категорическое требование, конечно, никогда не может быть выполнено в полной мере. Его следует понимать таким образом, что фактор, вносимый случайными ошибками измерения факторов 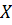в дисперсию воспроизводимости эксперимента, должен быть пренебрежимо мал по сравнению с действием других неконтролируемых факторов, образующих ошибку эксперимента.

2) Аддитивная помеха (шум эксперимента) 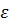является случайной величиной, распределенной по нормальному закону с математическим ожиданием 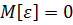и постоянной дисперсией 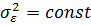. Значение помехи 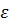в различных наблюдениях являются некоррелированными величинами.

3) При наличии параллельных опытов оценки дисперсий выходного параметра 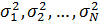должны быть однородны. Однородность оценок дисперсий при одинаковом числе параллельных опытов для каждой серии реализаций проверяют по критерию Кохрена, а при разном – по критерию Бартлетта.

4) Результаты наблюдений над выходной величиной 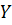представляют собой независимые, нормально распределенные случайные величины. Данное требование не является безусловным, так как метод наименьших квадратов можно применять для определения коэффициентов уравнения регрессии, если даже нет нормального распределения 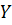, но при это уже ничего нельзя сказать о его эффективности, особенно при выборках малого объема. Поэтому целесообразно попытаться преобразовать случайную величину к нормальному закону.

Проверка предпосылок проведения регрессионного анализа

Выполнение основных предпосылок возможности проведения регрессионного анализа предопределено порядком проведения эксперимента. Так как эксперимент вычислительный, то ошибка фиксации (измерения) значений входных исследуемых факторов равна нулю. «Шум» эксперимента является случайной величиной, распределенной по нормальному закону с параметрами 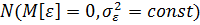, так как разброс метеофакторов моделировался нормальным законом распределения. Следовательно, и выходной параметр D также будет подчиняться нормальному закону распределения. Таким образом, следует проверить предпосылку – однородность оценок дисперсии выходного параметра.

Проверка предпосылки фактически сводится к проверке постоянства дисперсии «шума»:

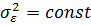
Считается, что это условие выполнено, если справедлива гипотеза

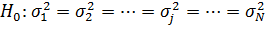
Проверка данной гипотезы при конкурирующей 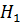хотя бы одна дисперсия 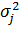не равна остальным, для одинакового числа параллельных опытов в каждой точке плана эксперимента, производится с помощью критерия Кохрена. Статистика G этого критерия имеет вид

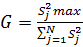(8)

С целью проверки нулевой гипотезы 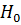по таблице значений G-критерия выбираем его критическое значение для заданного уровня значимости 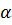, числа степеней свободы 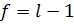и числа суммируемых оценок дисперсий, равного N.

Сравниваем расчетное и табличное значение G-критерия. Если выполняется условие 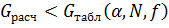(9)

(9)

то гипотеза об однородности ряда выборочных дисперсий выходного параметра не отвергается. Это означает, что для значимых различий и в качестве оценки дисперсии воспроизводимости эксперимента можно взять среднюю дисперсию, то есть

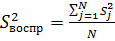(10)