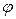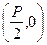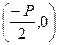Пусть прямая определяется заданием p и α (рис.4). Уравнение прямой в полярных координатах можно записать в виде:
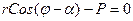 ,т.е.
,т.е. 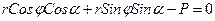
 r M(r, r M(r,  ) ) | |





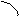

Но, учитывая связь полярных и прямоугольных координат, имеем:
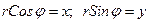
. Следовательно, полученное уравнение можно записать в окончательном виде:
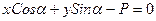
(1) - это нормальное уравнение прямой.

 Можно показать, как привести уравнение прямой
Можно показать, как привести уравнение прямой 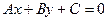 к виду (1). Для этого умножим уравнение прямой на некоторый множитель λ≠0.
к виду (1). Для этого умножим уравнение прямой на некоторый множитель λ≠0. 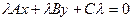 . Сопоставляя с (1) получим: y
. Сопоставляя с (1) получим: y

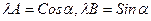 и
и 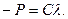
Из первых равенств можно найти λ
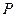

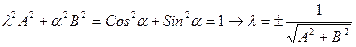
x
Нормирующий множитель λ согласно третьему равенству 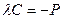 должен всегда иметь знак противоположный знаку свободного члена С.
должен всегда иметь знак противоположный знаку свободного члена С.
Угол между двумя прямыми
Пусть прямые L
1 и L
2 заданы уравнениями с угловыми коэффициентами (рис.5.)
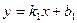
и
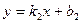
. Имеем
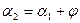
(теорема о внешнем угле треугольника) или
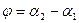
. Если
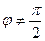
, то
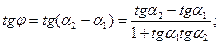
но tg
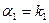
,
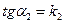
.
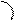
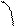



Получаем :

Точка пересечения прямых
Пусть даны две прямые 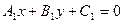 и
и 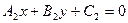 . Очевидно, что координаты их точки пересечения должны удовлетворять уравнению каждой прямой. Поэтому для того, чтобы их найти надо решить систему
. Очевидно, что координаты их точки пересечения должны удовлетворять уравнению каждой прямой. Поэтому для того, чтобы их найти надо решить систему
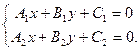
Если прямые не параллельны, то есть 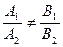 , то решение системы дает единственную точку пересечения прямых.
, то решение системы дает единственную точку пересечения прямых.
Расстояние от точки до прямой
Пусть задана точка M0(x0,y0) и прямая L, 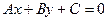 . Под расстоянием от M0 до прямой понимается длинна перпендикуляра d=M0N опущенного из т.M0 на прямую L.(Рис.6.)
. Под расстоянием от M0 до прямой понимается длинна перпендикуляра d=M0N опущенного из т.M0 на прямую L.(Рис.6.)

Расстояние d от т.M
0 до прямой L равно модулю проекции вектора M
1M
0 , гдеM
1(x
1,y
1) произвольная точка прямой на направление нормального вектора
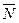
. Следовательно :

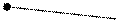

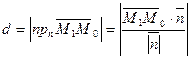
=

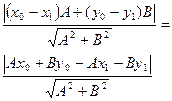
Так как M1(x1,y1) принадлежит прямой L, а 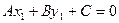 , то
, то 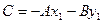 и окончательно получим :
и окончательно получим :
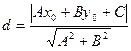 .
.
Линии второго порядка на плоскости.
Рассмотрим линии, определяемые уравнением второй степени относительно текущих координат
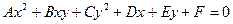 (1)
(1)
Коэффициенты уравнения действительные числа, но по крайней мере одно из чисел A,B или C отлично от 0. такие линии называют линиями (кривыми) второго порядка. Ниже мы покажем, что уравнение (1) определяет на плоскости окружность Эллипс, гиперболу или параболу.
Окружность
 Простейшей кривой второго порядка является окружность. Напомним, что окружность радиуса R с центром в точке M0 называется множество точек M плоскости удовлетворяющих условию MM0=R. Пусть точка M0 в системе Oxy имеет координаты x0,y0 ,а M(x,y)- произвольная точка окружности. Тогда
Простейшей кривой второго порядка является окружность. Напомним, что окружность радиуса R с центром в точке M0 называется множество точек M плоскости удовлетворяющих условию MM0=R. Пусть точка M0 в системе Oxy имеет координаты x0,y0 ,а M(x,y)- произвольная точка окружности. Тогда 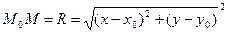 или
или
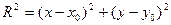 (1)
(1)
-каноническое уравнение окружности. Полагая, x0=y0=0 получим x2+y2=R2
покажем, что уравнение окружности можно записать в виде общего уравнения второй степени (1). Для этого возведем в квадрат правую часть уравнения окружности и получим:
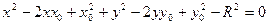
или
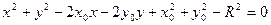
Для того чтобы это уравнение соответствовало (1) необходимо чтобы:
1) коэффициент B=0,
2) 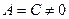 . Тогда получим:
. Тогда получим: 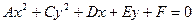 (2)
(2)
Последнее уравнение называется общим уравнением окружности. Поделив обе части уравнения на А ≠0 и дополнив члены содержащие x и y до полного квадрата получим:
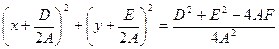 (2)
(2)
Сравнивая это уравнение с каноническим уравнением окружности, получим, что уравнение (2) действительно уравнение окружности если:
1)A=C, 2)B=0, 3)D2+E2-4AF>0.
При выполнении этих условий центр окружности расположен в точке О 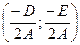 , а ее радиус
, а ее радиус 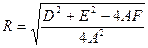 .
.
Эллипс
Эллипсом называется множество всех точек плоскости сумма расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная , большая чем расстояние между фокусами. Обозначим фокусы через F
1 и F
2 расстояние между ними 2c, а сумму расстояний от произвольной точки эллипса до фокусов через 2

(рис.1).


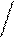

По определению 2

>2c, то есть

>c.для вывода уравнения эллипса будем считать, что фокусы F
1 и F
2 лежат на оси Ox, а т.O совпала с серединой отрезка F
1F
2 , тогда F
1(-c,0), F
2(c,0).
Пусть M(x,y)- произвольная точка эллипса, тогда, согласно определению эллипса MF1+MF2=2  то есть
то есть
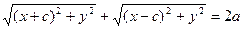 -это и есть уравнение эллипса. Можно его преобразовать к более простому виду следующим образом :
-это и есть уравнение эллипса. Можно его преобразовать к более простому виду следующим образом :
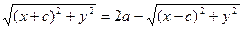 возводим в квадрат :
возводим в квадрат :
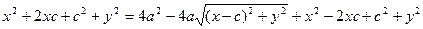
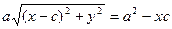
возводим в квадрат
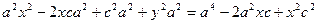
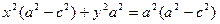 так как
так как 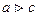 ,то
,то  2-c2>0 положим
2-c2>0 положим  2-c2=b2
2-c2=b2
Тогда последнее уравнение примет вид:
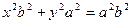
или

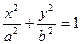
-это уравнение эллипса в каноническом виде.
Форма эллипса зависит от соотношения 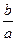 : при b=
: при b=  эллипс превращается в окружность. Уравнение примет вид
эллипс превращается в окружность. Уравнение примет вид 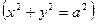 . В качестве характеристики эллипса часто пользуются отношением
. В качестве характеристики эллипса часто пользуются отношением 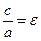 . Эта величина получила название эксцентриситета эллипса, причем, 0<
. Эта величина получила название эксцентриситета эллипса, причем, 0< 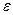 <1 так как 0<c<
<1 так как 0<c<  для окружности
для окружности 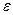 =1.
=1. 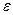 характеризует форму эллипса, чем меньше
характеризует форму эллипса, чем меньше 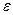 , тем эллипс будет менее сплющенным.
, тем эллипс будет менее сплющенным.
Исследование формы эллипса.
1) уравнение эллипса содержит x и y, только в четной степени, поэтому эллипс симметричен относительно осей Ox и Oy 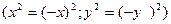 , а также относительно т.О (0,0), которую называют центром эллипса.
, а также относительно т.О (0,0), которую называют центром эллипса.
2) найдем точки пересечения эллипса с осями координат. Положив y=0 находим A1(  ,0) и A2(-
,0) и A2(-  ,0), в которых эллипс пересекает Ox. Положив x=0, находим B1(0,b) и B2(0,-b). Точки A1,A2,B1,B2 –называются вершинами эллипса. Отрезки A1A2 и B1B2 , а также их длины 2
,0), в которых эллипс пересекает Ox. Положив x=0, находим B1(0,b) и B2(0,-b). Точки A1,A2,B1,B2 –называются вершинами эллипса. Отрезки A1A2 и B1B2 , а также их длины 2  и 2b называются соответственно большой и малой осями эллипса. Числа
и 2b называются соответственно большой и малой осями эллипса. Числа  и b – соответственно большой и малой полуосями.
и b – соответственно большой и малой полуосями.
A1( 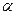 ,0) ,0) | |
A2(- 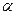 ,0) ,0) | |




3) из уравнения эллипса следует, что каждое слагаемое в левой части ≤1, то есть
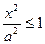
и
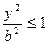
или
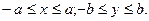
Следовательно, все точки эллипса лежат внутри прямоугольника, образованного прямыми x=±
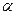
,y=±b. (Рис.2.)
4)В уравнении эллипса сумма неотрицательных слагаемых равна единице. Следовательно, при возрастании одного слагаемого, другое будет уменьшаться , то есть если |x| возрастает, то |y| - уменьшается и наоборот. Из всего сказанного следует, что эллипс имеет форму изображенную на рис.2. (овальная замкнутая кривая).
Гипербола.
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой точки которых до двух точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая чем расстояние между фокусами.






Обозначим фокусы через F
1 и F
2 расстояние между ними 2c, а модуль разности расстояний от каждой точки гиперболы до фокусов через 2
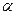
. По определению 2
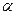
<2c то есть
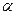
<c. Для вывода уравнения гиперболы выберем систему координат Oxy так, что фокусы F
1 и F
2 лежат на оси Ox ,а начало координат совпадает с серединой отрезка F
1F
2 (рис.3.)
Тогда F1(-c,0),F2(c,0).Пусть M(x,y)- произвольная точка гиперболы. Тогда согласно определению 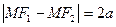 или
или 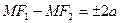 то есть
то есть 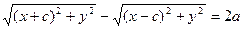 . После упрощения, аналогичных тем, которые мы делали при выводе уравнения эллипса, получим каноническое уравнение гиперболы:
. После упрощения, аналогичных тем, которые мы делали при выводе уравнения эллипса, получим каноническое уравнение гиперболы:

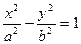 , где
, где 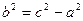 (1)
(1)
Исследование формы гиперболы по ее уравнению
1.Уравнение гиперболы содержит x и y в четной степени. Следовательно гипербола симметрична относительно осей Ox и Oy, а также т.O, которую называют центром гиперболы.
2.Найдем точки пересечения гиперболы с осями координат. Положив y=0, находим две точки пересечения гиперболы с осью Ox: A1(  ,0),A2(-
,0),A2(-  ,0). Положив x=0, получим y2=-b2 , чего не может быть. Следовательно, гипербола ось Oy не пересекает. Точки A1(
,0). Положив x=0, получим y2=-b2 , чего не может быть. Следовательно, гипербола ось Oy не пересекает. Точки A1(  ,0) и A2(-
,0) и A2(- 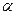 ,0) называются вершинами гиперболы, а отрезок A1A2=2
,0) называются вершинами гиперболы, а отрезок A1A2=2  - действительной полуосью гиперболы.
- действительной полуосью гиперболы.
Отрезок B1B2 (B1B2=2b), соединяющий точки B1(0,b) и B2(0,-b) , называется мнимой полуосью. Прямоугольник со сторонами 2  и 2b называется основным прямоугольником гиперболы.
и 2b называется основным прямоугольником гиперболы.
3. Из уравнения гиперболы следует, что уменьшаемое 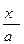 не меньше единицы, то есть
не меньше единицы, то есть 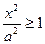 или
или 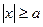 . Это означает, что точки гиперболы расположены справа от прямой x=
. Это означает, что точки гиперболы расположены справа от прямой x=  (правая ветвь) и слева от прямой x=-
(правая ветвь) и слева от прямой x=-  (левая ветвь).
(левая ветвь).




4. Из уравнения гиперболы видно, что когда |x| возрастает, то и |y| возрастает. Это следует из того, что разность
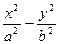
- сохраняет постоянное значение, равное единице. Из всего сказанного следует, что гипербола имеет форму изображенную на рис.4. (кривая, состоящая из двух неограниченных ветвей)
Асимптоты гиперболы
Прямая L называется асимптотой неограниченной кривой K, если расстояние d от точки M кривой до этой прямой стремится к 0 при неограниченном удалении т.M вдоль кривой K от начала координат.
На рис.4 приведена иллюстрация сказанного. Покажем, что гипербола 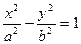 имеет две асимптоты:
имеет две асимптоты: 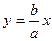 и
и 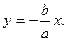
Так как эти прямые и гипербола симметричны относительно осей координат, то достаточно рассмотреть только точки указанных линий, расположенные в первой четверти. Возьмем на прямой 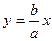 т.N, имеющую ту же абсциссу x, что и точка M(x,y) на гиперболе
т.N, имеющую ту же абсциссу x, что и точка M(x,y) на гиперболе
И найдем разность MN между ординатами прямой и ветви гиперболы(рис.5)


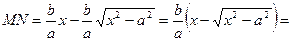



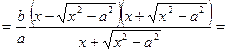


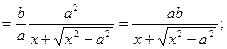
При возрастании x знаменатель дроби увеличивается, числитель=const. Стало быть, длинна MN→0, так как MN>d , то и d → 0. То есть 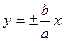 - асимптоты гиперболы.
- асимптоты гиперболы.
Эксцентриситетом гиперболы ( 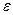 ) называется отношение расстояния между фокусами к величине действительной оси гиперболы :
) называется отношение расстояния между фокусами к величине действительной оси гиперболы :
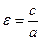 ,т.к. с≥
,т.к. с≥  , то
, то 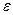 >1.
>1.
Эксцентриситет характеризует форму гиперболы. Чем меньше эксцентриситет , тем более вытянут ее основной прямоугольник.
Гиперболы 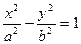 и
и 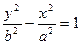 имеют общие асимптоты, такие гиперболы называются сопряженными.
имеют общие асимптоты, такие гиперболы называются сопряженными.
Парабола
Параболой называется множество всех точек плоскости, каждая из которых одинаково удалены от данной точки, называемой фокусом и данной прямой называемой директрисой. Расстояние от фокуса до директрисы называется параметром параболы и обозначается p(p>0). Для вывода уравнения параболы выберем системы координат Oxy так, чтобы ось Ox проходила через F перпендикулярно директрисе в направлении от директрисы к F а начало координат О расположим посредине между фокусом и директрисой(рис.6). В выбранной системе F имеет координаты 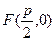 , а уравнение директрисы имеет вид
, а уравнение директрисы имеет вид 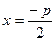 или
или 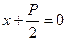 .
.


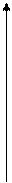



Пусть M(x,y) - произвольная точка параболы. Соединим т.M с F. Проведем отрезок MN перпендикулярный директрисе. Согласно определению параболы MF=MN. По формуле расстояния между точками находим
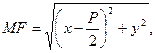
а
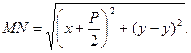
F 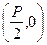 | |
N 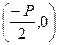 | |

Следовательно
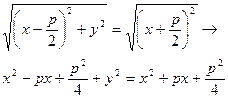 Возводя в квадра
Возводя в квадра  т
т
Отсюда 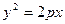 - каноническое уравнение параболы.
- каноническое уравнение параболы.
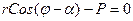 ,т.е.
,т.е. 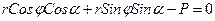






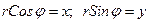 . Следовательно, полученное уравнение можно записать в окончательном виде:
. Следовательно, полученное уравнение можно записать в окончательном виде: 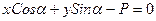 (1) - это нормальное уравнение прямой.
(1) - это нормальное уравнение прямой. 
 Можно показать, как привести уравнение прямой
Можно показать, как привести уравнение прямой 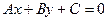 к виду (1). Для этого умножим уравнение прямой на некоторый множитель λ≠0.
к виду (1). Для этого умножим уравнение прямой на некоторый множитель λ≠0. 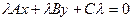 . Сопоставляя с (1) получим: y
. Сопоставляя с (1) получим: y
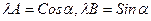 и
и 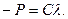
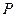

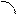
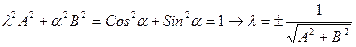 x
x 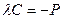 должен всегда иметь знак противоположный знаку свободного члена С.
должен всегда иметь знак противоположный знаку свободного члена С.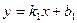 и
и 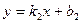 . Имеем
. Имеем 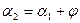 (теорема о внешнем угле треугольника) или
(теорема о внешнем угле треугольника) или 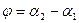 . Если
. Если 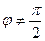 , то
, то 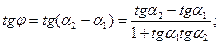 но tg
но tg 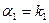 ,
, 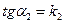 .
. 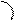
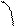
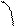


 Получаем :
Получаем : 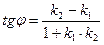

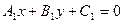 и
и 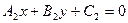 . Очевидно, что координаты их точки пересечения должны удовлетворять уравнению каждой прямой. Поэтому для того, чтобы их найти надо решить систему
. Очевидно, что координаты их точки пересечения должны удовлетворять уравнению каждой прямой. Поэтому для того, чтобы их найти надо решить систему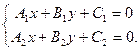
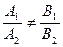 , то решение системы дает единственную точку пересечения прямых.
, то решение системы дает единственную точку пересечения прямых.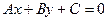 . Под расстоянием от M0 до прямой понимается длинна перпендикуляра d=M0N опущенного из т.M0 на прямую L.(Рис.6.)
. Под расстоянием от M0 до прямой понимается длинна перпендикуляра d=M0N опущенного из т.M0 на прямую L.(Рис.6.) Расстояние d от т.M0 до прямой L равно модулю проекции вектора M1M0 , гдеM1(x1,y1) произвольная точка прямой на направление нормального вектора
Расстояние d от т.M0 до прямой L равно модулю проекции вектора M1M0 , гдеM1(x1,y1) произвольная точка прямой на направление нормального вектора  . Следовательно :
. Следовательно : 

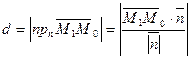 =
= 
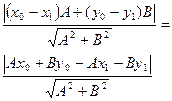
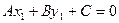 , то
, то 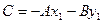 и окончательно получим :
и окончательно получим :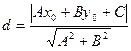 .
.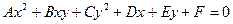 (1)
(1) Простейшей кривой второго порядка является окружность. Напомним, что окружность радиуса R с центром в точке M0 называется множество точек M плоскости удовлетворяющих условию MM0=R. Пусть точка M0 в системе Oxy имеет координаты x0,y0 ,а M(x,y)- произвольная точка окружности. Тогда
Простейшей кривой второго порядка является окружность. Напомним, что окружность радиуса R с центром в точке M0 называется множество точек M плоскости удовлетворяющих условию MM0=R. Пусть точка M0 в системе Oxy имеет координаты x0,y0 ,а M(x,y)- произвольная точка окружности. Тогда 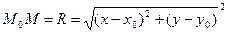 или
или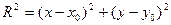 (1)
(1)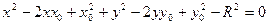
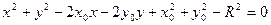
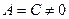 . Тогда получим:
. Тогда получим: 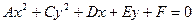 (2)
(2)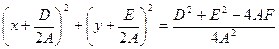 (2)
(2)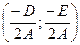 , а ее радиус
, а ее радиус 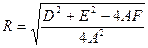 .
. (рис.1).
(рис.1). 

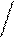
 По определению 2
По определению 2  >2c, то есть
>2c, то есть  >c.для вывода уравнения эллипса будем считать, что фокусы F1 и F2 лежат на оси Ox, а т.O совпала с серединой отрезка F1F2 , тогда F1(-c,0), F2(c,0).
>c.для вывода уравнения эллипса будем считать, что фокусы F1 и F2 лежат на оси Ox, а т.O совпала с серединой отрезка F1F2 , тогда F1(-c,0), F2(c,0).  то есть
то есть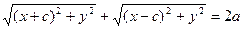 -это и есть уравнение эллипса. Можно его преобразовать к более простому виду следующим образом :
-это и есть уравнение эллипса. Можно его преобразовать к более простому виду следующим образом :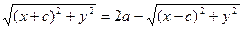 возводим в квадрат :
возводим в квадрат :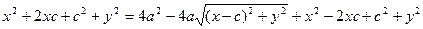
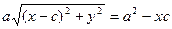
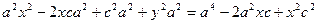
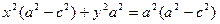 так как
так как 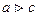 ,то
,то  2-c2>0 положим
2-c2>0 положим  2-c2=b2
2-c2=b2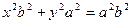

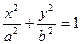
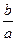 : при b=
: при b=  эллипс превращается в окружность. Уравнение примет вид
эллипс превращается в окружность. Уравнение примет вид 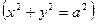 . В качестве характеристики эллипса часто пользуются отношением
. В качестве характеристики эллипса часто пользуются отношением 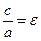 . Эта величина получила название эксцентриситета эллипса, причем, 0<
. Эта величина получила название эксцентриситета эллипса, причем, 0< 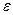 <1 так как 0<c<
<1 так как 0<c<  для окружности
для окружности 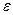 =1.
=1. 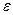 характеризует форму эллипса, чем меньше
характеризует форму эллипса, чем меньше 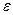 , тем эллипс будет менее сплющенным.
, тем эллипс будет менее сплющенным.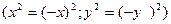 , а также относительно т.О (0,0), которую называют центром эллипса.
, а также относительно т.О (0,0), которую называют центром эллипса. ,0) и A2(-
,0) и A2(-  ,0), в которых эллипс пересекает Ox. Положив x=0, находим B1(0,b) и B2(0,-b). Точки A1,A2,B1,B2 –называются вершинами эллипса. Отрезки A1A2 и B1B2 , а также их длины 2
,0), в которых эллипс пересекает Ox. Положив x=0, находим B1(0,b) и B2(0,-b). Точки A1,A2,B1,B2 –называются вершинами эллипса. Отрезки A1A2 и B1B2 , а также их длины 2  и 2b называются соответственно большой и малой осями эллипса. Числа
и 2b называются соответственно большой и малой осями эллипса. Числа  и b – соответственно большой и малой полуосями.
и b – соответственно большой и малой полуосями.


 3) из уравнения эллипса следует, что каждое слагаемое в левой части ≤1, то есть
3) из уравнения эллипса следует, что каждое слагаемое в левой части ≤1, то есть 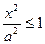 и
и 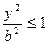 или
или 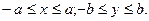
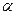 ,y=±b. (Рис.2.)
,y=±b. (Рис.2.) 




 Обозначим фокусы через F1 и F2 расстояние между ними 2c, а модуль разности расстояний от каждой точки гиперболы до фокусов через 2
Обозначим фокусы через F1 и F2 расстояние между ними 2c, а модуль разности расстояний от каждой точки гиперболы до фокусов через 2 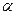 . По определению 2
. По определению 2 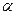 <2c то есть
<2c то есть 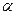 <c. Для вывода уравнения гиперболы выберем систему координат Oxy так, что фокусы F1 и F2 лежат на оси Ox ,а начало координат совпадает с серединой отрезка F1F2 (рис.3.)
<c. Для вывода уравнения гиперболы выберем систему координат Oxy так, что фокусы F1 и F2 лежат на оси Ox ,а начало координат совпадает с серединой отрезка F1F2 (рис.3.) 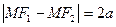 или
или 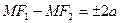 то есть
то есть 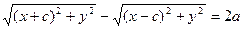 . После упрощения, аналогичных тем, которые мы делали при выводе уравнения эллипса, получим каноническое уравнение гиперболы:
. После упрощения, аналогичных тем, которые мы делали при выводе уравнения эллипса, получим каноническое уравнение гиперболы:
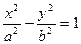 , где
, где 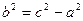 (1)
(1) ,0),A2(-
,0),A2(-  ,0). Положив x=0, получим y2=-b2 , чего не может быть. Следовательно, гипербола ось Oy не пересекает. Точки A1(
,0). Положив x=0, получим y2=-b2 , чего не может быть. Следовательно, гипербола ось Oy не пересекает. Точки A1(  ,0) и A2(-
,0) и A2(- 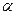 ,0) называются вершинами гиперболы, а отрезок A1A2=2
,0) называются вершинами гиперболы, а отрезок A1A2=2  - действительной полуосью гиперболы.
- действительной полуосью гиперболы. и 2b называется основным прямоугольником гиперболы.
и 2b называется основным прямоугольником гиперболы.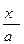 не меньше единицы, то есть
не меньше единицы, то есть 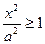 или
или 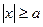 . Это означает, что точки гиперболы расположены справа от прямой x=
. Это означает, что точки гиперболы расположены справа от прямой x=  (правая ветвь) и слева от прямой x=-
(правая ветвь) и слева от прямой x=-  (левая ветвь).
(левая ветвь).




 4. Из уравнения гиперболы видно, что когда |x| возрастает, то и |y| возрастает. Это следует из того, что разность
4. Из уравнения гиперболы видно, что когда |x| возрастает, то и |y| возрастает. Это следует из того, что разность 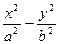 - сохраняет постоянное значение, равное единице. Из всего сказанного следует, что гипербола имеет форму изображенную на рис.4. (кривая, состоящая из двух неограниченных ветвей)
- сохраняет постоянное значение, равное единице. Из всего сказанного следует, что гипербола имеет форму изображенную на рис.4. (кривая, состоящая из двух неограниченных ветвей)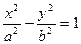 имеет две асимптоты:
имеет две асимптоты: 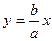 и
и 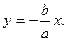
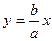 т.N, имеющую ту же абсциссу x, что и точка M(x,y) на гиперболе
т.N, имеющую ту же абсциссу x, что и точка M(x,y) на гиперболе

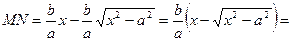



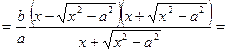


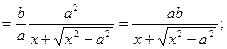

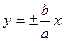 - асимптоты гиперболы.
- асимптоты гиперболы.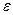 ) называется отношение расстояния между фокусами к величине действительной оси гиперболы :
) называется отношение расстояния между фокусами к величине действительной оси гиперболы :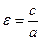 ,т.к. с≥
,т.к. с≥  , то
, то 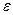 >1.
>1.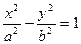 и
и 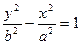 имеют общие асимптоты, такие гиперболы называются сопряженными.
имеют общие асимптоты, такие гиперболы называются сопряженными.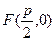 , а уравнение директрисы имеет вид
, а уравнение директрисы имеет вид 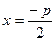 или
или 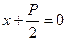 .
.



 Пусть M(x,y) - произвольная точка параболы. Соединим т.M с F. Проведем отрезок MN перпендикулярный директрисе. Согласно определению параболы MF=MN. По формуле расстояния между точками находим
Пусть M(x,y) - произвольная точка параболы. Соединим т.M с F. Проведем отрезок MN перпендикулярный директрисе. Согласно определению параболы MF=MN. По формуле расстояния между точками находим 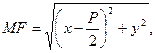 а
а 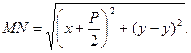
 Следовательно
Следовательно 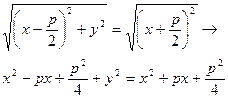 Возводя в квадра
Возводя в квадра  т
т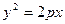 - каноническое уравнение параболы.
- каноническое уравнение параболы.
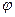 )
)