Краткие теоретические сведения

Чайковский филиал

Государственного образовательного учреждения высшего профессионального образования

"Пермский государственный технический университет"

(ЧФ ПГТУ)

Кафедра гуманитарных и естественно-научных дисциплин

Лаборатория физики

Механика

Лабораторная работа №2

“Определение вязкости жидкости методом Стокса”

Цель работы: Измерить коэффициент вязкости жидкости.

Приборы и принадлежности: стеклянный цилиндр с исследуемой жидкостью, шарики, штангенциркуль, секундомер, миллиметровая линейка.

Краткие теоретические сведения.

При движении жидкости между ее соседними слоями, движущимися с разными скоростями, возникают силы внутреннего трения, действующие таким образом, чтобы уровнять скорости всех слоев. Возникновение этих сил объясняется тем, что слои, движущиеся с разными скоростями, обмениваются молекулами. Молекулы из более быстрого слоя передают более медленному некоторое количество движения (импульс), вследствие чего он начинает двигаться быстрее. Молекулы из более медленного слоя получают в быстром слое некоторое количество движения, что приводит к торможению быстрого слоя. При переносе импульса от слоя к слою происходит изменение импульса всех слоев. Это значит, что на каждый из слоев действует сила, равная изменению импульса в единицу времени (второй закон Ньютона).

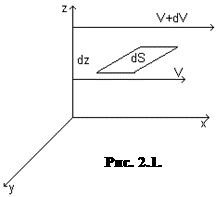Рассмотрим жидкость, движущуюся в направлении оси х (рис. 2.1) Пусть на расстоянии dz скорости потока отличаются на величину dv.

Отношение dv/dz характеризует изменение скорости потока в направлении оси z и называется градиентом скорости.

Таким образом, градиент скорости численно равен изменению скорости на единицу длины в направлении, перпендикулярном скорости.

Согласно закону Ньютона, сила внутрен­него трения (вязкости), действующая между двумя слоями, пропорциональна площади их соприкосновения S и гра­диенту скорости:

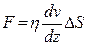(2.1)

Величина h (“эта”) называется коэффициентом внутреннего трения, или коэффициентом динамической вязкости.

Если в формуле (2.1) положить численно dv/dz = 1 и DS = 1, то F = h, т.е. коэффициент динамической вязкости численно равен силе внутреннего трения, возникающей на каждой единице поверхности соприкосновения двух слоев, движущихся относительно друг друга с градиентом скорости, равным единице.

В системе СИ единицей измерения коэффициента динамической вязкости ηявляется (Па·с).

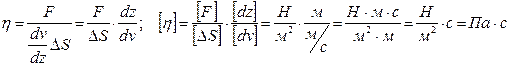
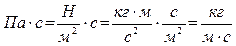
В системе СГС единицей измерения коэффициента динамической вязкости ηявляется:

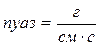
Соотношение единиц измерения коэффициента динамической вязкости η в системах СИ и СГС:

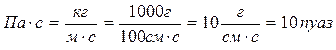
Коэффициент динамической вязкости h зависит от природы жидкости и для конкретной жидкости с повышением температуры уменьшается.

Наряду с коэффициентом динамической вязкости h часто употребляют коэффициент кинематической вязкости n = h /r, где r – плотность жидкости.

Кинематическая вязкость в системе СИ измеряется в м²/с.

В системе СГС единицей измерения кинематической вязкости являетсястокс = см²/с.

В табл. 1 приведены значения вязкости некоторых жидкостей при различных температурах:

Таблица 1

t, °С	(h, 10-3 Па×с)
Вода	Глицерин	Масло касторовое	Ртуть
- 20	---	---	---	1,86
	1,788		---	1,69
	---	---	3760,0	---
	1,306		2418,0	---
	1,140	---	1514,0	---
	1,004		950,0	1,55
	0,894	---	621,0	---
	0,801		451,0	1,50
	---	---	312,0	---
	0,653		231,0	---
	0,549		---	1,41
	0,470		---	---
	0,406		---	---
	0,356		---	---
	0,316		---	---
	0,283		16,9	1,24
	---	---	---	1,05
	---	---	---	0,95

Силами внутреннего трения в жидкости обусловлено сопротивление, которое испытывает твердое тело при движении относительно жидкости.

Аналитическое решение задачи нахождения силы сопротивления является очень сложным. Подобная задача была решена английским физиком Стоксом лишь для случая очень медленного движения шарика в безграничном объеме жидкости. Сила сопротивления в этом случае оказалась равной следующей величине:

F = 6p×h×r×v, (2.2)

где r – радиус шарика;

v – скорость шарика относительно части жидкости, находящейся в покое.

Метод Стокса.

Формула Стокса (2.2) позволяет определить коэффициент динамической вязкости h, если известны другие величины. Метод определения коэффициента динамической вязкости с помощью уравнения (2.2) называется методом Стокса.