Вычисление точечных оценок
Занятие № 2
Вычисление статистических оценок
Цели зянятия:
1. Изучить применение встроенных функций MS Excel для получения оценок числовых характеристик случайных величин.
2. Ознакомиться с инструментом Пакета анализа MS Excel «Описательная статистика».
Основные положения
Точечной статистической оценкой параметра a распределения случайной величины называется приближённое значение 
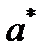 этого параметра, вычисленное по статиcтическим данным.
этого параметра, вычисленное по статиcтическим данным.
Наиболее часто вычисляются следующие оценки: среднее арифметическое выборки (выборочное среднее), выборочная медиана, выборочная дисперсия, выборочные асимметрия и эксцесс.
При оценивании неизвестных параметров наряду с точечными оценками используются также интервальные оценки. Интервальная оценка 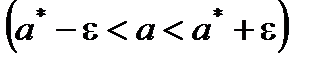 представляет собой интервал со случайными границами
представляет собой интервал со случайными границами 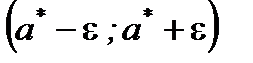 , который с заданной вероятностью γ накрывает неизвестное истинное значение параметра
, который с заданной вероятностью γ накрывает неизвестное истинное значение параметра 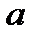 . При этом должно выполняться равенство:
. При этом должно выполняться равенство:
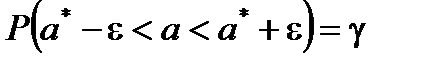 .
.
Интервал 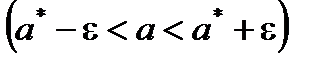 называют доверительным интервалом (интервальной оценкой) для параметра
называют доверительным интервалом (интервальной оценкой) для параметра  с доверительной вероятностью γ, а
с доверительной вероятностью γ, а  и
и 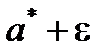 соответственно нижней и верхнейграницами интервальной оценки, а число ε – точностью оценки.
соответственно нижней и верхнейграницами интервальной оценки, а число ε – точностью оценки.
Вычисление точечных оценок
Для выборки объёма n: 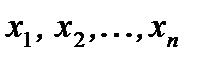 среднее арифметическое равно
среднее арифметическое равно
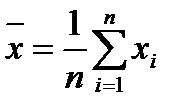
Для сгруппированной выборки 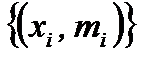 , где
, где 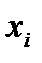 ─ варианты,
─ варианты, 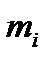 ─ частоты,
─ частоты, 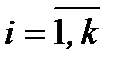 , k ─ число вариант (для интервального статистического ряда
, k ─ число вариант (для интервального статистического ряда 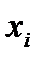 ─ середины интервалов, а k ─ число интервалов), выборочное среднее определяется по формуле:
─ середины интервалов, а k ─ число интервалов), выборочное среднее определяется по формуле:
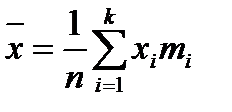
Среднее арифметическое значение является статистической оценкой математического ожидания.
В MS Excel для вычисления выборочного среднего несгруппированной выборки используется функция (категория Статистические): СРЗНАЧ(число1;число2; …), где: число1; число2; … ─ от 1 до 30 аргументов, для которых вычисляется среднее.
Для сгруппированной выборки сначала вычисляют сумму произведений вариант и соответствующих частот с помощью функции: СУММПРОИЗВ(массив1;массив2;…) (категория Математические), а затем делят на объём выборки.
Пример 1. Найти выборочное среднее для выборки из 10 значений: 3; 0; 0; 2; 1; 4; 0; 4; 3; 2.
Последовательность выполнения
1. Ввести исходную выборку в ячейки А2:А11.
2. В ячейку А12 ввести формулу =СРЗНАЧ(А2:А11). В ячейке А12 появится результат: 1,9.
Пример 2. Найти выборочное среднее для выборки, представленной статистическим рядом:
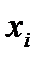 | -2 | -1 | ||||||||
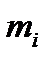 |
Последовательность выполнения
1. Ввести значения вариант 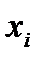 в ячейки С2:С11, а значения соответствующих частот
в ячейки С2:С11, а значения соответствующих частот 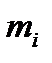 в ячейки D2:D11.
в ячейки D2:D11.
2. В ячейку C12 ввести формулу
=СУММПРОИЗВ(С2:С11;D2:D11)/СУММ(D2:D11).
Функция СУММ() находится в категории Математические. В ячейке С12 появится результат: 3,571429.
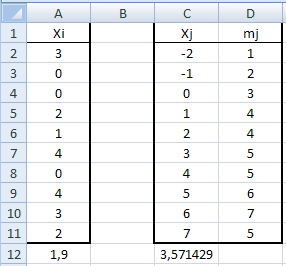
Медианой Me называется такое значение признака, которое делит ранжированный ряд на две равные части.
Для дискретного вариационного ряда значение медианы определяется по формуле:
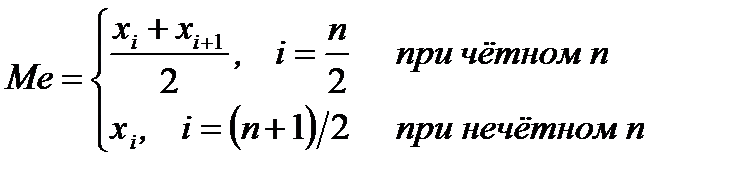
Для интервального статистического ряда сначала определяют номер медианы как полусумму частот 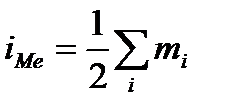 . Затем отсчитывают накопленные частоты и находят первый интервал
. Затем отсчитывают накопленные частоты и находят первый интервал 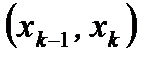 , для которого накопленные частоты
, для которого накопленные частоты 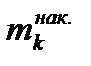 не меньше номера медианы
не меньше номера медианы 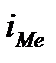 . Медиана определяется с помощью интерполяционной формулы:
. Медиана определяется с помощью интерполяционной формулы:
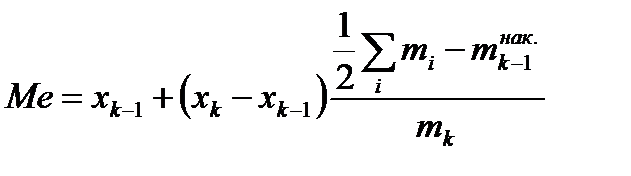
В MS Excel для вычисления медианы дискретного ряда применяется функция (категория Статистические):
МЕДИАНА(число1;число2; …),
где: число1;число2; … ─ от 1 до 30 аргументов, для которых вычисляется медиана.
Пример 3. Найти медиану дискретного ряда:
1; 0; 6; 2; 4; 4; 1; 3; 4; 5; 6; 7; 2; 5; 4; 1; 2; 0; 0; 6.
Последовательность выполнения
1. Ввести исходную выборку в ячейки А1:А20.
2. В ячейку С1 ввести формулу =МЕДИАНА(А1:А20). В ячейке С1 появится результат: 3,5.
3. Осуществить проверку. Для этого выделить диапазон А1:А20. Выбрать во вкладке Главная на панели Редактирование команды Сортировка и фильтр → Сортировка от минимального к максимальному. Так как число членов ряда чётное, то медиана вычисляется как полусумма десятого и одиннадцатого значений: (3+4)/2 = 3,5.
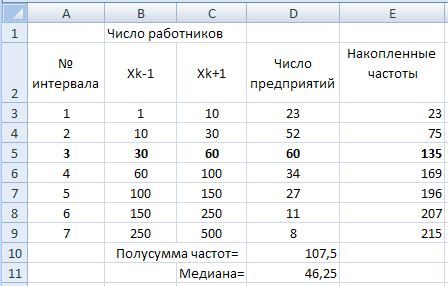
Пример 4. Найти медиану для интервального статистического ряда, который показывает распределение предприятий региона по численности работников.
| № интервала | Число работников | Число предприятий |
| 1─10 | ||
| 11─30 | ||
| 31─60 | ||
| 61─100 | ||
| 101─150 | ||
| 151─250 | ||
| 251─500 |
Последовательность выполнения
1. Ввести данные в диапазоне А1:D9.
2. В ячейку D10 ввести формулу =СУММ(D3:D9)/2.
3. В ячейку E3ввести формулу =D3, а в ячейку E4 ─ формулу =E3+D4.
4. Протянуть ячейку Е4 маркером заполнения до Е9. Медианным интервалом является интервал № 3.
5. В ячейку D11 ввести формулу =B5+(C5-B5)*(D10-E4)/D5.
Появится результат ─ значение медианы: 46,25.
Оценками характеристик рассеивания являются выборочная дисперсия и выборочное среднеквадратическое отклонение.
Выборочная дисперсия 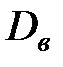 для сгруппированной в статистический ряд выборки определяется по формуле:
для сгруппированной в статистический ряд выборки определяется по формуле:
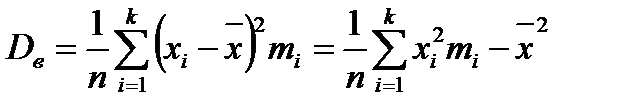
Исправленная выборочная дисперсия 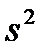 вычисляется по формуле:
вычисляется по формуле:
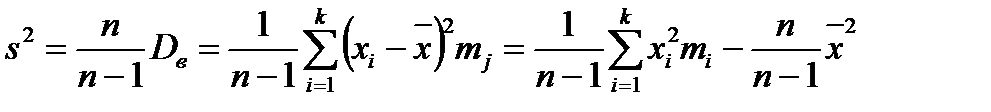
Если выборка не сгруппирована, то выборочная дисперсия определяется по формуле:
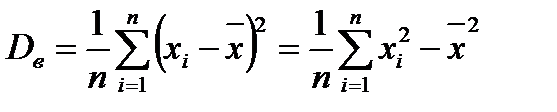 ,
,
а исправленная выборочная дисперсия 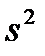 ─ по формуле:
─ по формуле:
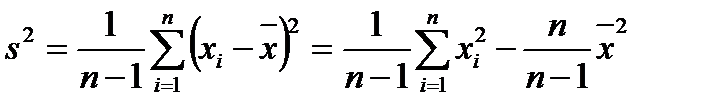 .
.
