Теңдікте квадрат жақшаның ішінде тұрған

(28)

матрицасының

(29)

түріндегі айқын максималды рангты нөлдік бөлгіші болады, яғни

(30)

бұлар канондық деп аталады.

Тікелей есептеулер жүргізу арқылы (26) матрицаның оң жақ нөлдік бөлгіші мына түрге ие болады:

(31)

ал (26) А матрицасының сол жақ нөлдік бөлгіші

(32)

түріне ие болады.

Осылайша берілген тік бұрышты матрицаның нөлдік бөлгіштерін табу үшін (26) бойынша базистерді түрлендіру матрицасын құрса жеткілікті, ал содан кейін (31) және/немесе (32) формулалар бойынша нөлдік бөлгіштерді құру керек.

Мысал 7. (канондық матрицаның нөлдік бөлгіштері). 6-мысалдағы матрицасының құрылымына сәйкес (27) теңдіктің оң жағында (бір нөлдік жол және екі нөлдік баған) 5-мысалдағы матрицасы екі нөлдік бөлгіші болады. Олардың канондық түрі мынадай:

Бұдан әрі (31) және (32) формулалары бойынша оң жақ және сол жақ нөлдік бөлгіштерді аламыз:

(33)

нөлдік бөлгіші алдында көрсетілген бағаннан тұратынын ескере кетейік. (5 мысал)

(25) түріндегі формулалар бойынша алынған матрицаларды кез келген матрицаға көбейтіндісі эквивалентті нөлдік бөлгіштер жиынын құрады:

және түрлендіру базистерінің матрицаларын құру үшін матрицаларды элементар түрлендіруге негізделген екі әдісті қолдануға болады.

Матрицаның жолына (бағанына) кез келген элементар түрлендіру жүргізу бұл матрицаны сол жағынан (оң жағынан) элементар деп аталатын қандай да бір P(Q) матрицасына көбейтумен тепе – тең.

Элементар түрлендіру матрицалары бірлік матрицадан алынады, егер оған сәйкес элементар түрлендіру жүргізсе.

Сол жақ және оң жақ элементар амалдарды және сәйкес матрицаларды символдық белгілейік:

сол жақ амалдар:

1. матрицаның 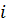-ші жолын нөлден өзгеше санына көбейту: ;

2. матрицаның 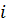-ші жолына нөлден өзгеше санына көбейтілген 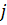-шы жолын қосу: ;

3. 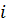-ші және 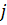-шы жолдарының орнын ауыстыру: ;

оң жақ амалдар:

1. Матрицаның 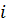-ші бағанын нөлден өзгеше санына көбейту: ;

2. Матрицаның матрицаның 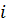-ші бағанына нөлден өзгеше санына көбейтілген 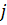-шы бағанына қосу: ;

3. Матрицаның 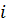-ші және 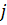-шы бағандарының орнын ауыстыру: .

Бірінші әдіс элементар матрицалар арқылы эквивалентті түрлендіру матрицаларын құрастыру.

А матрицасының жол және бағандарына элементар түрлендіру жүргізгенде матрицалық жазылуы мына түрге ие болады:

(34)

Мысал 8. (нөлдік бөлгіштерді құрастырудың бірінші әдісі). (21) матрицаға кез келген дұрыс элементар түрлендіру тізбегін қолданып канондық базиске келтіреміз (сонымен қатар элементар амалдарға символдық белгілеулерді қолданамыз)

Қолданылған элементар түрлендірудің нақты варианттары мен тізбегі соңғы нәтижеге еш әсер етпейді.

Әрбір элементар түрлендіруге сәйкес элементар түрлендіру матрицасын сәйкес қойып, жолдарға орындалған элементар амалдарды олардың ретін сақтай отырып, матрицалық түрде жазып және оларды бір – біріне көбейтеміз. Нәтижесінде координатының түрлендіру матрицасын аламыз:

Матрицаның бағандарына да осындай элементар түрлендіру жүргізіп, координатының түрлендіру матрицасын аламыз:

Координаттарды түрлендіру матрицасының екеуі де жалғыз еместік қасиетінің негізінде алдыңғы жазылған варианттардан өзгеше болады. (6-мысал). Сонымен қоса, оларды (31) және (32) формулаларда қолдану (33) нөлдік бөлгіштердің сол мәнін береді.

Әрбір элементар матрица элементар түрлендірулер жүргізгеннен кейін бірлік матрицадан алынғандықтан, онда түрлендіру матрицаларын сондай-ақ келесі түрде құруға болады: А матрицасын түріне келтіретін бірнеше элементар түрлендірулерді тауып, бірлік марицаның жолдарына элементар түрлендіруді сол ретпен жүргізіп, ал бағандарға жүргізілетін барлық элементар түрлендірулерді дәл сол ретпен бірлік матрицасына қолдану. Бұл түрлендірулерді келесі схемаларды қолданып жүргізу ыңғайлы.

Екінші әдіс. Нөлдің бөлгіші анықталатын матрица сол жағынан және астынан бірлік матрицамен толырылады, сонда мынадай конструкция алынады:

(35)

Бұл формальді түрде матрица болып табылмайды, ал оның түрі ашылған планшетке ұқсас.

Енді А матрицасының жолдары мен бағандарына, сонымен қатар оған қосылған бірлік матрицаларға элементар түрлендіру қолданайық. Түрлендірудің мақсаты А матрицасын канондық базис түрінде жазылуға әкелу. Түрлендірудің нәтижесінде мынадай конструкция алынады:

(36)

мұндағы

(37)

Сонымен қатар, матрицасының нөлдік блоктарына қарсы алғашқы бірлік матрицаның блоктары максималды рангты нөлдік бөлгіштен тұрады. матрицасының сол жағында сол жақ бөлгіш ал асында – оң жақ бөлгіш орналасқан:

(38)

(38) оң жақ жоғары бұрышында тұрған матрицасында нөлдік жолдың немесе нөлдік бағанның болмауы, А матрицасында сол немесе оң жақ нөлдік бөлгіш жоқ дегенді білдіреді.

Мысал 9. (Нөлдік бөлгішті құрудың екінші әдісі (планшет)). Қарасырылған (21) мысал үшін (35) конструкция мына түрге ие болады:

Бұл планшеттің жолдары мен бағандарына элементар түрлендіру жүргізу нәтижесінде мынаны аламыз:

(39)

Мұнда алдында (21) матрица үшін анықталған максималды рангты нөлдік бөлгішке тең блоктар белгіленген.

Матрицаларды канондау

(28) теңдікті (37) ескері п блоктар бойынша жазайық:

Анықтама 4. Рангы r –ға тең оң жағынан және сол жағынан төмендегі формула бойынша біруақытта көбейтілген, рангы r –ға тең А матрицасын бірлік матрицасына әкелетін , және тік бұрышты матрицаларын сәйкесінше сол жақ және оң жақ канонизаторы деп атаймыз:

(40)

Сол жақ және оң жақ канонизаторлар жол және бағанның сәйкесінше барлық сызықты тәуелсіз комбинациясын сипаттайды.

(24) қасиетке сәйкес нөлдік бөлгіштерді тапқанда канонизаорлардың әрқайсысы сәйкес канонизаторлар жиынының элементі болып табылады, яғни

мұндағы - кез келген элементтері бар қажетті өлшемді матрицалар.

Мысал 10. (сан матрицасының канонизаторы). (39) қолданып және сәйкес есептеулерді орындап, қарастырылып отырған (21) марица үшін (40) теңдікті қанағаттандыратындығына көз жеткізуге болады, яғни

Анықтама 5. өлшемді және рангы r –ға тең тік бұрышты А матрицасының жинақтылық канонизаторы деп А матрицасының оң жақ және сол жақ канонизаторының көбейтіндісіне тең өлшемді матрицаны айтады:

(42)

Жинақтылық канонизатор жолдар мен бағандар жиынтығының барлық сызықық тәуелсіз комбинациясын сипаттайды.

Мысал 11. (Сандық матрицаның сводный канонизаторы). 5-мысалдағы (21) матрица үшін сводный канонизатор (39), (42) –ге сәйкес мына түрге ие болады:

.

Осылайша, кез келген А матрицасына жалпы жағдайда, құрамында максималды рангты сол жақ және оң жақ нөлдік бөлгіштер және сондай-ақ сводный канонизатор болатын, жалғыз емес матрицалар үштігін, яғни

(43)

және (қажет болған жағдайда) матрицалар төрттігін

(44)

сәйкес қоюға болады.

Кез келген матрицаның бұлай берілуін матрицаны канондау деп атаймыз.

Дәріс 15,16

ТҮЙІНДЕС БЕЙНЕЛЕУ