Экспериментальная установка. Схема установки представлена на рисунке ниже:

Схема установки представлена на рисунке ниже:

Проволока 1 натянута между упорами 3-4 внутри трубки 2. Трубка имеет двойные стенки, между которыми циркулирует вода с заданной температурой. Температура стенок трубки поддерживается термостатом 10, который управляется с пульта 12. Нить нагревается электрическим током, ее температура определяется по изменению электрического сопротивления. Нить 1 включена в схему измерительного моста Уитстона, состоящего из магазина сопротивлений 8, гальванометра 9, нагрузочного 7 и эталонного сопротивлений 6. Параметры моста подобраны таким образом, что при балансе моста сопротивление магазина сопротивлений в 10 раз больше сопротивления нити. Вся схема подключена к источнику питания Е, параметры которого задаются с пульта 11.

Технические характеристики установки:

- диаметр проволоки (1) 0,1 мм;

- внутренний диаметр трубки (5) 8 мм;

- длина проволоки (1) 0,5 м;

- материал проволоки вольфрам;

- коэффициент температурного сопротивления

- величина R_эт 3,5 Ом;

- величина r_н 35 Ом.

ЗАДАНИЕ

1. Запустите работу.

2. Снимите при комнатной температуре зависимость сопротивления нити R от протекающего через установку тока I. Провести измерения для 4¸5 минимальных значений напряжения.

Результаты измерений занести в таблицу №1:

Физ. величина	TR	U	I	R
Ед. измерений Номер опыта	К	В	А	Ом

Постройте график зависимости . Продлите график до пересечения с осью ординат, для определения значения сопротивления нити при I = 0. Запишите определенное значение R_o - сопротивление проволоки при комнатной температуре.

3. Нажать кнопки «Нагрев» и «Цирк». Для различных температур стенок трубки T_R (20°, 40°, 60°, 80°) проведите измерения зависимости сопротивления нити R от протекающего через установку тока I при различных значениях напряжения, от минимального (1 В) до максимального (15 В), увеличивая напряжение с шагом 2¸3 вольта. Записывайте в таблицу значения установленного напряжения V, протекающего тока I, сопротивления проволоки R.

4. Для каждого набора значений предыдущего упражнения рассчитать поток тепла, переносимый воздухом с проволоки:

[2]

и температуру поверхности проволоки: [3]

Используя результаты вычислений по формулам [2] и [3] рассчитать по формуле [1] среднеинтегральные коэффициенты теплопроводности c(T_ср),

где - среднеарифметическая температура.

5. Постройте график зависимости . Сравните полученные значения с табличными.

Результаты измерений и вычислений занести в таблицу №2:

Физ. величина	TR	U	I	R	Q	Tr	Tср	c
Ед. измерений   Номер опыта	оС	В	А	Ом	Вт	К	К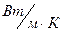
№	знач.	№	знач.
		1. 2. 3. 4. 5.		1. 2. 3. 4. 5.
		…	…	…	…
		…	…	…	…
		…	…	…	…

6) рассчитать погрешность косвенных измерений;

7) привести окончательный результат.

Работа № 18 Определение теплопроводности твердого тела (пластина)

Цель работы: определение коэффициента теплопроводности твердых тел методом сравнения с теплопроводностью эталонного материала.

Количество теплоты , протекающее за единицу времени через однородную перегородку толщиной и площадью при разности температур , определяется формулой

[1]

где c - коэффициент теплопроводности, характеризующий свойства среды.

Значение коэффициента теплопроводности c может быть определено непосредственно из формулы [1], если измерить на опыте величины DQ, DT, d и S. Однако точное определение DQ практически невозможно, поэтому в настоящей работе производится сравнение теплопроводности исследуемого материала с теплопроводностью некоторого другого эталонного материала с хорошо известным значением коэффициента c. При этом можно избежать измерения DQ. Суть метода следующая. Две пластинки, изготовленные из материалов с коэффициентами теплопроводности c₁ и c₂, зажимаются между стенками, температуры которых равны T₁ и T₂ и поддерживаются постоянными во время опыта. Если толщины пластинок (d₁ и d₂) достаточно малы по сравнению с наименьшим линейным размером их поверхности, то можно пренебречь потерей тепла через боковые поверхности. Тогда можно считать, что тепловой поток протекает только от горячей стенки к холодной через пластины. В этом случае

и [2]

Из [2] получаем окончательно [3]

где DT₁ и DT₂ - перепады температур на пластинках.

Зная теплопроводность материала одной из пластинок, используя формулу [3] легко определить на опыте теплопроводность другой пластинки. Необходимо помнить о том, что формула [3] получается в предположении сохранения теплового потока неизменным через обе пластинки, что оправдано при толщине, очень малой по сравнению с радиусом пластинки, и при теплоизоляции боковых поверхностей пластинок.