ЛИНЕЙН(Значения_y; Значения_x; Конст; статистика)

Значения_y - массив значений y.

Значения_x- необязательный массив значений x, если массив х опущен, то предполагается, что это массив {1;2;3;...} такого же размера, как и Значения_y.

Конст - логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если Конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом. Если аргумент Конст имеет значение ЛОЖЬ, то b полагается равным 0 и значения a подбираются так, чтобы выполнялось соотношение y = ax.

Статистика - логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. Если аргумент статистика имеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику. Если аргумент статистика имеет значение ЛОЖЬ или опущен, то функция ЛИНЕЙН возвращает только коэффициент a и постоянную b.

Для вычисления множества точек на линии регрессии используется функция ТЕНДЕНЦИЯ.

ТЕНДЕНЦИЯ(Значения_y; Значения_x; Новые_значения_x; Конст)

Значения_y- массив значений y, которые уже известны для соотношения y = ax + b.

Значения_x- массив значений x.

Новые_значения_x- новый массив значений, для которых ТЕНДЕНЦИЯ возвращает соответствующие значения y. Если Новые_значения_x опущены, то предполагается, что они совпадают с массивом значений х.

Конст - логическое значение, которое указывает, требуется ли, чтобы константа b была равна 0. Если Конст имеет значение ИСТИНА или опущено, то b вычисляется обычным образом. Если Конст имеет значение ЛОЖЬ, то b полагается равным 0, и значения а подбираются таким образом, чтобы выполнялось соотношение y = ax. Необходимо помнить, что результатом функций ЛИНЕЙН, ТЕНДЕНЦИЯ является множество значений - массив.

Для расчета коэффициента корреляции используется функция КОРРЕЛ, возвращающая значения коэффициента корреляции:

КОРРЕЛ(Массив1;Массив2)

Массив1 - массив значений y.

Массив2 - массив значений y.

Массив1 и Массив2 должны иметь одинаковое количество точек данных.

ПРИМЕРИзвестна табличная зависимость G(L). Построить линию регрессии и вычислить ожидаемое значение в точках 0, 0.75, 1.75, 2.8, 4.5.

L		0,5		1,5		2,5		3,5
G		2,39	2,81	3,25	3,75	4,11	4,45	4,85	5,25

Введем таблицу значений в лист MS Excel и построим точечный график. Рабочий лист примет вид изображенный на рис.

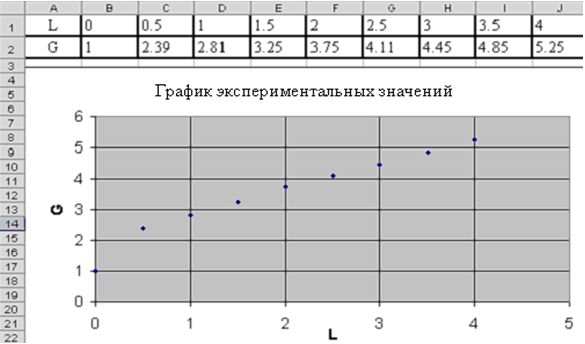Рис.

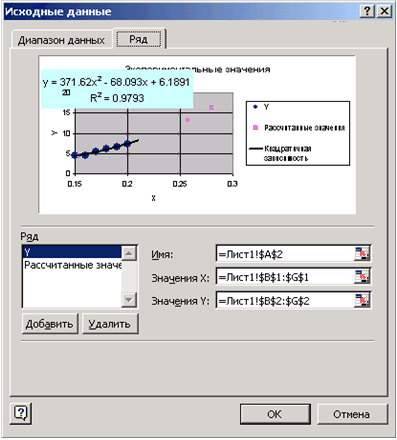
Для того, чтобы рассчитать значения коэффициентов регрессии а и b выделим ячейки К2:L2, обратимся к мастеру функций и в категории Статистические выберем функцию ЛИНЕЙН. Заполним появившееся диалоговое окно так, как показано на рис. и нажмем Ок.

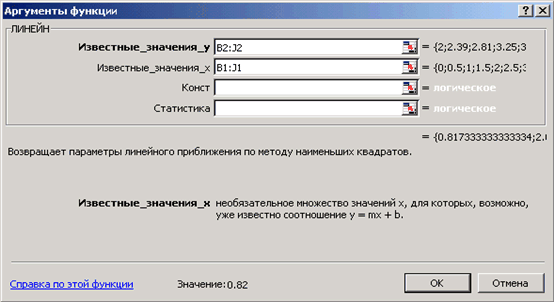В результате вычисленное значение появится только в ячейке К2. Для того чтобы вычисленное значение появилось и в ячейке L2 необходимо войти в режим редактирования, нажав клавишу F2, а затем нажать комбинацию клавиш CTRL+SHIFT+ENTER.

Для расчета значения коэффициента корреляции в ячейку M2 была введена следующая формула: М2 = КОРРЕЛ(B1:J1;B2:J2)

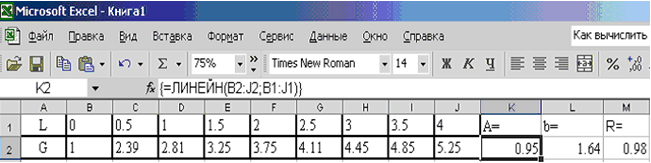Для вычисления ожидаемого значения в точках 0, 0.75, 1.75, 2.8, 4.5 занесем их в ячейки L9:L13. Затем выделим диапазон ячеек M10:M13 и введем формулу:

= ТЕНДЕНЦИЯ(B2:J2;B1:J1;L9:L13).

Для того чтобы вычисленные значения появились и в ячейках M10:M13 необходимо нажать комбинацию клавиш CTRL+SHIFT+ENTER.

Рис.

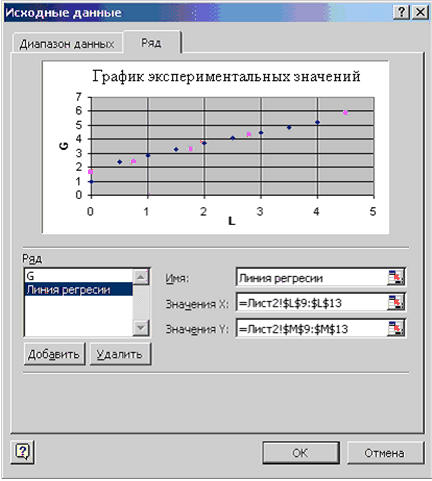
Изобразим линию регрессии на диаграмме. Для этого выделим экспериментальные точки на графике, щелкнем правой кнопкой мыши и выберем команду Исходные данные. В появившемся диалоговом окне, для добавления линии регрессии щелкнем по кнопке Добавить.

В качестве имени введем Линия регрессии, в качестве Значения Х: L9:L13, в качестве Значения Y: M9:M13. Далее выделяем линию регрессии, для изменения ее типа щелкаем правой кнопкой мыши и выбираем команду Тип диаграммы. Для форматирования линии регрессии (можно изменить толщину линии, цвет, тип маркера и т.п) дважды щелкаем по ней

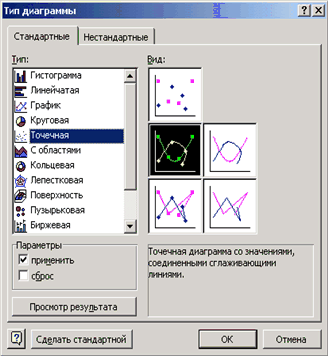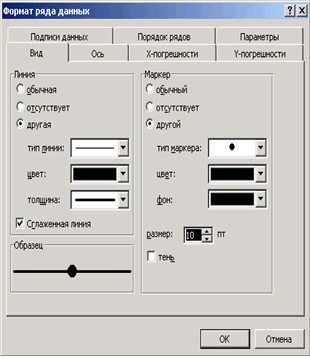Рис.	Рис.

После форматирования графика рабочий лист примет вид, изображенный на рис.

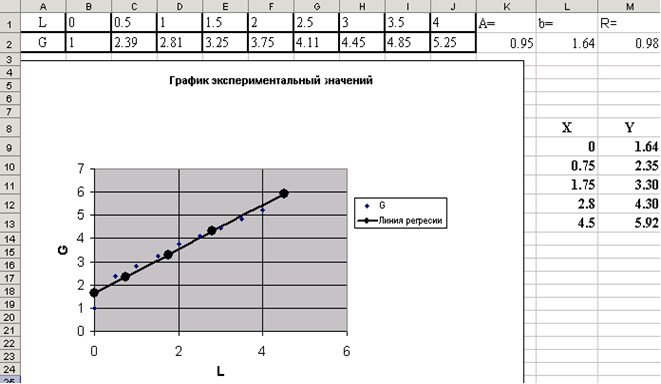Рис.

Квадратичная функция

Необходимо определить параметры функции y = a_o + a₁x + a₂x₂.

Составим функцию:

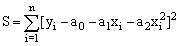Для этой функции запишем систему уравнений:

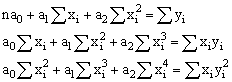Для нахождения параметров a_o, a₁, a₂ необходимо решить систему линейных алгебраических уравнений.

Кубическая функция

Необходимо определить параметры многочлена третьей степени y = a_o + a₁ x + a₂ x₂ + a₃ x₃.

Составим функцию S:

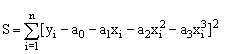Система уравнений для нахождения параметров a_o, a₁, a₂, a₃ имеет вид:

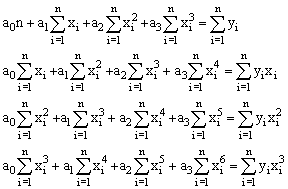Для нахождения параметров a_o, a₁, a₂, a₃ необходимо решить систему четырёх линейных алгебраических уравнений.

Если в качестве аналитической зависимости выберем многочлен k-й степени y = a_o+a₁x+...+a_k x^k, то система уравнений для определения параметров a_i принимает вид:

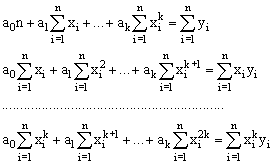Подбор параметров функции y = a x^b

Для нахождения параметров функции y = a x^b проведем логарифмирование функции y: Ln y = Ln a + b Ln x

Сделаем замену Y = ln y; X = ln x. Получим линейную зависимость Y = A + b X. Найдем коэффициенты линии регрессии A и b.определяем a = e^A. Мы получили значение параметров функции y = ax^b.

Подбор параметров функции y = ae^bx

Прологарифмируем выражение y = ae^bx: Ln y = Ln a + bx Ln e;

Проведём замену Y = Ln y, A = Ln a. Вновь получаем линейную зависимость Y = bx+A. Найдем A и b. Затем определим a = e^A .

Ниже приведены замены переменных, которые преобразовывают функции вида y = f (x, a, b) к линейной зависимости Y = Ax+B.

Y = f(x,a,b)	Замена

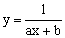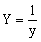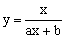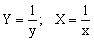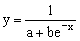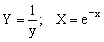Подбор параметров функции y =a^xb e^cx

Прологарифмируем выражение y = a^xb e^cx, после логарифмирования оно принимает вид:

Ln(y) = Ln(a)+b Ln(x)+cx Ln(e)

Сделаем замену Y=Ln(y), A=Ln(a). После замены выражение принимает вид:

Y = A+b Ln(x)+cx

Для функции составим функцию S:

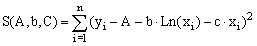Параметры A, b и c следует выбрать таким образом, чтобы функция S была минимальной.

Получим систему трёх линейных алгебраических уравнений для определения коэффициентов A, b и c.

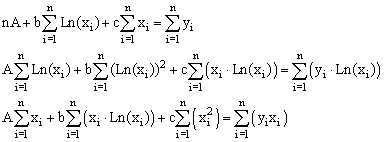Решив систему, получим значения A, b, c. После чего вычисляем a=e^A.

Построение различных аппроксимирующих зависимостей в MS Excel реализовано в виде свойства диаграммы - линия тренда.

ПРИМЕР. В результате эксперимента была определена некоторая табличная зависимость. Выбрать и построить аппроксимирующую зависимость. Построить графики табличной и подобранной аналитической зависимости. Вычислить ожидаемое значение в указанных точках.

x1 = 0,1539, x2 = 0,2569, x3 = 0,28
X	0,15	0,16	0,17	0,18	0,19	0,20
Y	4,4817	4,4930	5,4739	6,0496	6,6859	7,3891

Решение задачи можно разбить на следующие этапы:

1. Ввод исходных данных и построение точечного графика

2. Добавление к этому графику линии тренда.

Рассмотрим этот процесс подробно.

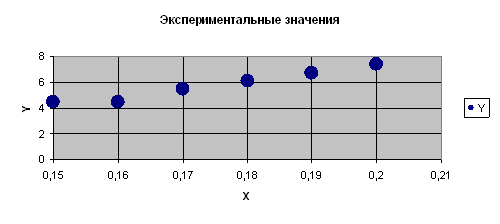Рис.

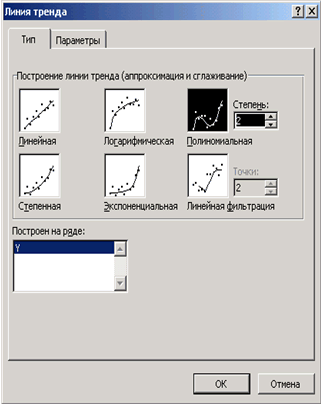
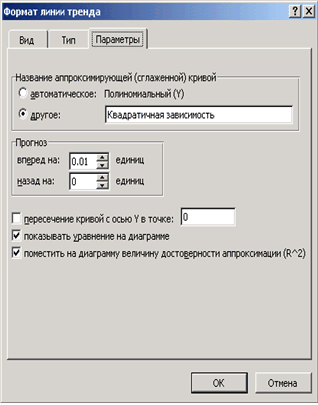
Выделим экспериментальные точки на графике, щелкнем правой кнопкой мыши и воспользуемся командой Добавить линию тренда. Появившееся диалоговое окно позволяет построить аппроксимирующую зависимость. На первой вкладке этого окна указывается вид аппроксимирующей зависимости (в нашем случае необходимо выбрать полиномиальную зависимость второй степени). На второй определяются параметры построения:

• Название аппроксимирующей зависимости.
• Прогноз вперед (назад) на n единиц (этот параметр определяет, на какое количество единиц вперед (назад) необходимо продлить линию тренда).
• Показывать ли точку пересечения кривой с прямой Y = const.
• Показывать аппроксимирующую функцию на диаграмме или нет (параметр показывать уравнение на диаграмме).
• Помещать ли на диаграмму величину среднеквадратичного отклонения или нет (параметр поместить на диаграмму величину достоверности аппроксимации).

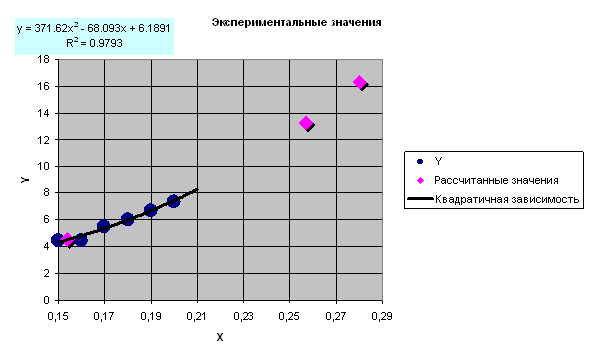
На рис. изображена полученная диаграмма.

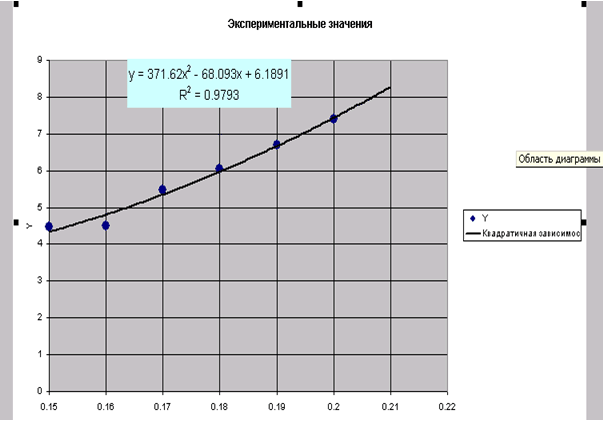Рис.

Для расчета ожидаемых значений в точках 0.1539, 0.2569, 0.28 введем эти значения в ячейки B4:D4. В ячейку B5 введем формулу подобранной аппроксимирующей зависимости (=371.62*B4^2-68.093*B4+6.1891) и скопируем ее в ячейки C5, D5. Фрагмент рабочего листа примет вид:

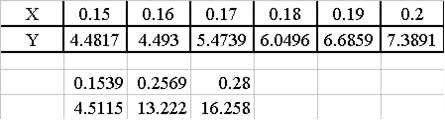Добавим полученные расчетные значения на диаграмму. Для этого на диаграмме выделим экспериментальные значения, щелкнем правой кнопкой мыши и выберем команду Исходные данные. Добавим туда Рассчитанные значения

Аналогично с помощью линии тренда можно подобрать и параметры других типов зависимостей (линейной, логарифмической и экспоненциальной и т. д.).

ПРИМЕР.В результате эксперимента получена зависимость z(t):

T	0,66	0,9	1,17	1,47	1,7	1,74	2,08	2,63	3,12
Z	38,9	68,8	64,4	66,5	64,95	59,36	82,6	90,63	113,5

Подобрать коэффициенты зависимости Z(t)=At⁴+Bt³+Ct²+Dt+K методом наименьших квадратов.

Эта задача эквивалентна задаче нахождения минимума функции пяти переменных:

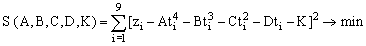Введем табличную зависимость в рабочий лист MS Excel и построим график функции

Рассмотрим процесс решения задачи оптимизации . Пусть значения А, В, С, D и К хранятся в ячейках K1:K5. В ячейку B23 введем значение функции At⁴+Bt³+Ct²+Dt+K в первой точке (ячейка B1):

B23 = $K$1*B1^4 + $K$2*B1^3 + $K$3*B1^2 + $K$4*B1 + $K$5.

Получим ожидаемое значение (в начале 0) в точке B1. Затем растянем эту формулу на весь диапазон B23:J23. В ячейку B24 введем формулу, вычисляющую квадрат разности между экспериментальными и расчетными точками:

B24 = (B23-B2)^2,

и растянем ее на диапазон B24:J24. В ячейке В25 будем хранить суммарную квадратичную ошибку. Для этого введем формулу:

В25 = СУММ(B24:J24).

Теперь осталось с помощью решающего блока (Сервис Поиск решения) решить задачу оптимизации без ограничений, заполнив соответствующим образом появившееся диалоговое окно.

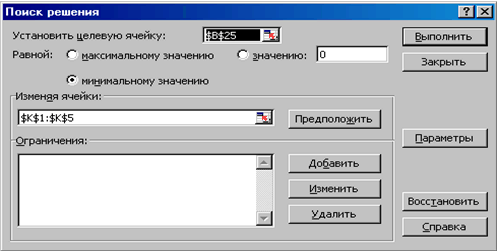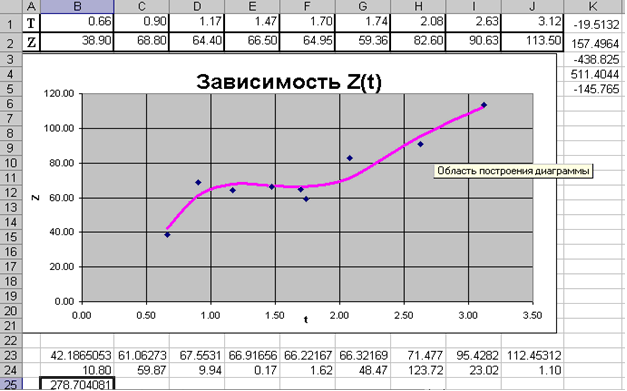
Результатом работы решающего блока будет вывод в ячейки K1:K5 значений параметров функции At⁴+Bt³+Ct²+Dt+K. В ячейках B23:J23 получим ожидаемые значение функции в исходных точках. Поместим эти точки в виде отдельной линии на графике. В ячейке B25 будет храниться суммарная квадратичная ошибка.

По мнению авторов, использование решающего блока - это один из эффективных способов реализации метода наименьших квадратов с помощью MS Excel.

ВАРИАНТЫ ЗАДАНИЙ

1. На первом рабочем листе документа MS Excel ввести исходные данные, соответствующие варианту задания. Проанализировать экспериментальную зависимость. Построить график экспериментальных точек.

2. На втором рабочем листе средствами MS Excel рассчитать коэффициенты регрессии, коэффициент корреляции, среднеквадратичные отклонения и суммарную ошибку. Построить в одной графической области экспериментальные точки и линию регрессии.

3. Третий рабочий лист должен содержать вычисление коэффициентов функциональной зависимости, соответствующей варианту задания. Расчет коэффициентов произвести аналитически при помощи метода наименьших квадратов, сведя задачу к задаче оптимизации. Построить в одной графической области экспериментальные точки и график подобранной функциональной зависимости. Определить суммарную ошибку.

4. На четвертом рабочем листе построить линию тренда, если это возможно. Убедится в том, что вычисленные в п.3 коэффициенты совпадают с коэффициентами линии тренда. Провести сравнительный анализ полученных результатов и построить в одной графической области график экспериментальных точек, линию регрессии и график полученной экспериментальной зависимости.

5. Озаглавить рабочие листы согласно тематике вычислений. Исходные данные, результаты вычислений и графики сопровождать соответствующими подписями и пояснениями.

Вариант №1. P(s)=As³+Bs²+Сs+D

s	0,00	1,00	1,50	2,00	2,50	3,00	3,50	4,00	4,50	5,00
P	10,00	50,10	39,58	15,40	23,68	33,60	57,78	100,90	149,50	256,00

Вариант № 2. G(s)=Ae^bs

s	0,5	1,5		2,5		3,5		4,5
G	3,99	5,65	6,41	7,71	11,215	17,611	27,83	38,19	39,3

Вариант № 3. K(s)=As^b

s	0,5		1,5		2,5		3,5
K	1,65	2,1		2,1	2,3	2,4	2,22	2,59

Вариант № 4. V(s)=As^bе^Cs

s	0,2	0,7	1,2	1,7	2,2	2,7	3,2
V	2,3198	2,9569	2,3999	6,4357	6,5781	6,9459	14,6621

Вариант № 5. W(s)=A/(Bs+C)

s
W	0,529	0,298	0,267	0,171	0,156	0,124	0,1	0,078	0,075

Вариант № 6. Q(s)=As²+Bs+C

s		1,25	1,5	1,75		2,25	2,5	2,75
Q	5,21	4,196	3,759	3,672	4,592	4,621	5,758	7,173	9,269

Вариант № 7. Y=x/(Ax-B)

x		3,1	3,2	3,3	3,4	3,5	3,6	3,7	3,8	3,9
Y	0,61	0,6	0,592	0,58	0,585	0,583	0,582	0,57	0,572	0,571

Вариант № 8. V=1/(A+Be^-U)

u		2,5		3,5		4,5		5,5
V	5,197	7,78	11,14	15,09	19,24	23,11	26,25	28,6	30,3

Вариант № 9. R=At^B+14,5

t
R	2,11	5,2	5,15	19,27	18,2	30,37			30,22	31,2

Вариант № 10. R=Ch²+Dh+K

h
R	0,035	0,09	0,147	0,1	0,24	0,28	0,31	0,34

Вариант №11. G=DL+K

l		0,5		1,5		2,5		3,5
G		2,39	2,81	3,25	3,75	4,11	4,45	4,85	5,25

Вариант № 12. Y=Ax³+Bx²+Cx+D

x		1,5		2,5		3,5		4,5
Y	14,5		26,9	83,75	89,9	219,1	326,1		637,5

Вариант № 13. Y=Ax³+Cx+D

x		1,5		2,5		3,5		4,5
Y	6,5	20,38	46,4	88,63	151,1	237,9		500,3	684,5

Вариант № 14. R=Ch²+K

h		1,5		2,5		3,5		4,5
R	7,5	14,25	23,7	25,86	50,7	68,25	88,5	111,5

Вариант № 15. Z=At⁴+Ct²+K

t		1,5		2,5		3,5		4,5
Z	2,2	10,6	35,6		191,1	359,2	618,7	997,9	1598,5

Вариант № 16. Z=At⁴+Bt³+Dt+K

t		1,5		2,5		3,5		4,5
Z	2,21	9,83	30,5	74,5	155,2	288,86	494,5	794,69	1214,6

Вариант № 17. Z=At⁴+Bt³+Ct²+K

t		1,5		2,5		3,5		4,5
Z	5,25	13,4	31,29	64,64	121,23	209,94	341,23	527,14

Вариант № 18. Z=At⁴+Dt+K

t	0,4	0,6	0,8		1,2	1,4	1,6	1,8
Z	0,5	1,35	2,37	3,8	5,8	8,65	12,57	18,05	0,86

Вариант № 19. Y=Ax³+D

x		0,2	0,4	0,6	0,8		1,2	1,4	1,6	1,8
Y	3,6	3,59	3,65	3,96	4,12	4,86	5,67	6,85	8,42	10,47

Вариант № 20. R=At^B

t		1,5		2,5		3,5		4,5
R	2,19	14,8	57,15	163,2	384,5	793,5		2585,5	4242,22

Вариант № 21. W(s)=1/(Bs-C)

s		1,5		2,5		3,5		4,5
W	0,19	0,17	0,15	0,14	0,13	0,12	0,11	0,1	0,9

Вариант № 22. V(s)=s^bе^Cs

s		1,1	1,2	1,3	1,4	1,5	1,6	1,7	1,8	1,9
V			52,5	83,5	130,2	202,5

Вариант № 23. Y(x)=x/(Ax+B)

x		1,5		2,5		3,5		4,5
Y	0,214	0,221	0,2237	0,2258	0,2262	0,2268	0,2275	0,2283	0,2288

Вариант № 24. V(s)=Asе^Cs

s
V	43,75	32,25	17,83	8,76		1,77	0,76	0,32

Вариант № 25. V(s)=As^bе^s

s		1,5		2,5		3,5		4,5
V	6,5	8,71	12,67	18,6	27,63	42,61	65,6	101,86

Вариант № 26. V=(A+Be^U)

u		0,5		1,5		2,5		3,5
V	3,597	4,597	5,5984	7,5987	11,269		26,5096	42,1599

Вариант №27. G(L)=D/L+K

L		1,13	1,25	1,38	1,5	1,63	1,75	1,88
G	3,8	3,2	2,6	2,2	1,8	1,6	1,4	1,3	1,1

Вариант № 28. V(s)=As^B

s		2,3	2,9	4,1	5,2	5,9	6,8	8,1	9,2
V	2,4	2,9	58,5	165,5	337,5		754,5

Вариант № 29. K(s)=Ae^Sb

s		0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8
K	2,2	3,73	6,25	10,49	17,61	29,65	49,84	140,9	237,1

Вариант № 30. Z(t)=At⁵+Bt⁴+Ct³+Dt²+Kt+L

t	0,66	0,9	1,17	1,47	1,7	1,74	2,08	2,63	3,12
Z	38,9	68,8	64,4	66,5	64,95	59,36	82,6	90,63	113,5

Вариант № 31. R(T) = At⁵+Bt⁴+Ct³+Dt²+L

T
R	0,035	0,09	0,147	0,1	0,24	0,28	0,31	0,34

Вариант №32. G (t) = At⁵+Bt⁴+Dt²+Kt+L

t		0,5		1,5		2,5		3,5
G		2,39	2,81	3,25	3,75	4,11	4,45	4,85	5,25

Вариант № 33. Y (t)= At⁵+Ct³+Dt²+Kt+L

t		1,5		2,5		3,5		4,5
Y	14,5		26,9	83,75	89,9	219,1	326,1		637,5

Вариант № 34. Y (t) = At⁵+Bt⁴+Ct³+Kt+L

x		1,5		2,5		3,5		4,5
Y	6,5	20,38	46,4	88,63	151,1	237,9		500,3	684,5

Вариант № 35 R (t) = At⁵+Ct³+Kt

t		1,5		2,5		3,5		4,5
R	2,19	14,8	57,15	163,2	384,5	793,5		2585,5	4242,22

Вариант № 36. R(t) = At⁵+Dt²+Kt

t		1,5		2,5		3,5		4,5
R	2,19	14,8	57,15	163,2	384,5	793,5		2585,5	4242,22

Вариант № 37. W(T) = At⁵+Dt²+L

T		1,5		2,5		3,5		4,5
W	0,19	0,17	0,15	0,14	0,13	0,12	0,11	0,1	0,9

Вариант № 38. V= At⁵+L

T		1,1	1,2	1,3	1,4	1,5	1,7	1,8	1,9
V			52,5	83,5	130,2	202,5