Вероятность случайного события.

Сравнивая между собой случайные события, мы часто говорим, что одно из них более вероятно (имеет больше шансов наступить, в большей степени возможно), чем другое. Например: при игре в карты при сдаче каждому игроку 6 карт событие получить 2 туза более вероятно, чем получить 4 туза.

Чтобы придать подобным сравнениям количественный смысл, необходимо с каждым событием связать число, выражающую степень возможности данного события.

Пусть А есть случайное событие по отношению к данному опыту. Пусть данный опыт произведен N раз и при этом случайное событие А наступило N(А) раз.

Число N(А) называется частотой события А в рассматриваемой серии опытов.

Составим отношение:

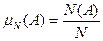.(1)

Оно называется относительной частотой наступления события А в N опытах.

Оказывается, для весьма многих (практически для всех) случайных массовых событий А относительная частота обладает свойством устойчивости, которое состоит в том, что в нескольких сериях из достаточно больших наблюдений события А (в одних и тех же условиях) мы обычно имеем приближённые равенства

.

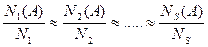Это означает, что с увеличением числа опытов N, относительная частота 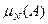стабилизируется (колеблется около одного и того же числа), приближаясь к некоторой постоянной P(A), которая характеризует данное случайное событие А. Естественно считать, что эта постоянная и измеряет степень возможности наступления события А. Она называется вероятностью события А. Итак мы получили следующее:

Определение. Вероятность случайного события А - это связанное с данным событием постоянное число, обозначаемое через P(А), около которого колеблется относительная частота наступления этого события в длинных сериях опытов.

Это определение можно выразить в виде формулы:

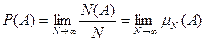. (2)

Замечание. Необходимо предостеречь от неправильного понимания формулы (2). В этой формуле отнюдь не утверждается , что предел равен P(A). Что для сколь угодно малого , начиная с некоторого номера N0, будет выполнятся неравенство . Эту формулу мы должны понимать следующим образом: если выполнить большое число серий опытов, состоящих из достаточно большого количества опытов, то для подавляющего большинства серий относительная частота будет отличатся от P(A) меньше чем на . Однако могут существовать и такие «исключительные» серии для которых сильно отличается от P(A). «Исключительные» серии составляют незначительную часть от общего числа серий. Поэтому можно считать практически достоверным, что наша серия (при большом N) не окажется «исключительной» и что в ней будет близко к P(A).