Краткие теоретические сведения. Во многих практических задачах закон распределения изучаемой случайной величины X (ГС) неизвестен и возникает задача выбора закона распределения
Во многих практических задачах закон распределения изучаемой случайной величины X (ГС) неизвестен и возникает задача выбора закона распределения, согласующегося с результатами наблюдения над случайной величиной.
Пусть из ГС извлечена выборка объема n, причем значение 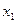 наблюдалось
наблюдалось 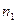 раз,
раз, 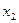 -
- 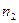 раз, …,
раз, …, 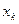 -
- 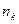 раз, где
раз, где 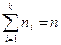 . Фактические наблюдаемые частоты
. Фактические наблюдаемые частоты 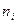 называются эмпирическими частотами.
называются эмпирическими частотами.
Пусть имеется основание предположить, что изучаемая случайная величина X распределена по некоторому закону. Это предположение, называемое гипотезой, определяется сущностью изучаемого явления, а также результатами предварительной обработки наблюдений (формами полигонов и гистограмм, соотношениями между выборочными характеристиками и т.д.). В общем случае статистической гипотезой называется каждое непротиворечивое множество предположений, относящихся к распределению случайной величины X.
Для того, чтобы проверить согласуется ли выдвинутая гипотеза о распределении изучаемой величины X с данными наблюдений, вычисляют теоретические частоты 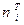 наблюдаемых значений, т.е. находят теоретически сколько раз величина X должна была принять каждое из наблюдаемых значений, если верна гипотеза.
наблюдаемых значений, т.е. находят теоретически сколько раз величина X должна была принять каждое из наблюдаемых значений, если верна гипотеза.
Обычно эмпирические и теоретические частоты различаются. Это различие может быть связано лишь с неизбежным влиянием случайных факторов при проведении наблюдений и обработке их результатов и не противоречить принятой гипотезе о законе распределения случайной величины, т.е. являться незначимым. Возможно, что расхождение частот неслучайно (значимо) и объясняется тем, что теоретические частоты вычислены, исходя из неверной гипотезы о законе распределения и ее необходимо пересмотреть.
Для проверки гипотезы о виде закона распределения случайной величины используются также специально подобранные случайные величины, распределения которых известны. Они называются критериями согласия.При этом задаются уровнем значимости, т.е. достаточно малой вероятностью 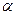 того, что будет отвергнута принятая гипотеза, хотя она и является верной. Для проверки гипотезы о виде закона распределения случайной величины используются также специально подобранные случайные величины, распределения которых известны. Они называются критериями согласия. При этом задаются уровнем значимости, т.е. достаточно малой вероятностью
того, что будет отвергнута принятая гипотеза, хотя она и является верной. Для проверки гипотезы о виде закона распределения случайной величины используются также специально подобранные случайные величины, распределения которых известны. Они называются критериями согласия. При этом задаются уровнем значимости, т.е. достаточно малой вероятностью 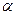 того, что будет отвергнута принятая гипотеза, хотя она и является верной.
того, что будет отвергнута принятая гипотеза, хотя она и является верной.
Рассмотрим применение одного из критериев согласия — критерия согласия Пирсона к проверке гипотезы о нормальном распределении изучаемой случайной величины.
С этой целью сравним эмпирические и теоретические (вычисленные в предположении нормального распределения) частоты. Один из способов нахождения теоретических частот нормально распределенной случайной величины состоит в следующем.
Сначала по выборочным данным находят 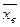 и
и 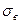 . Затем вычисляют теоретические частоты
. Затем вычисляют теоретические частоты 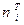 по формуле
по формуле 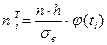
где п — объем выборки, h — длины частичного интервала, 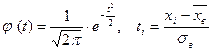 .
.
Значения функции 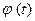 находят по таблице значений функции
находят по таблице значений функции 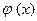 Теоретические частоты округляют до целых значений. Строят полигоны эмпирических и теоретических частот.
Теоретические частоты округляют до целых значений. Строят полигоны эмпирических и теоретических частот.
В качестве критерия проверки гипотезы применяют случайную величину
.
Данная величина называется «хи квадрат». Ясно, что чем меньше различаются эмпирические и теоретические частоты, тем меньше величина критерия 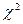 и, следовательно, он характеризует близость эмпирического и теоретического распределений. При употреблении критерия согласия Пирсона важное значение имеет правильный подсчет числа степеней свободы. Число степеней свободы k находят по равенству k = s – r - 1, где s - число частичных интервалов выборки; r - число параметров предполагаемого распределения, которые оценены по данным выборки. В частности, если предполагаемое распределение — нормальное, то оценивают два параметра (математическое ожидание и среднее квадратичное отклонение), поэтому r = 2 и число степеней свободы равно k = s – 2-1 = s -3.
и, следовательно, он характеризует близость эмпирического и теоретического распределений. При употреблении критерия согласия Пирсона важное значение имеет правильный подсчет числа степеней свободы. Число степеней свободы k находят по равенству k = s – r - 1, где s - число частичных интервалов выборки; r - число параметров предполагаемого распределения, которые оценены по данным выборки. В частности, если предполагаемое распределение — нормальное, то оценивают два параметра (математическое ожидание и среднее квадратичное отклонение), поэтому r = 2 и число степеней свободы равно k = s – 2-1 = s -3.
Для того, чтобы при заданном уровне значимости проверить гипотезу о нормальном распределении ГС вычисляют наблюдаемое значение критерия 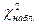 по таблице критических точек распределения
по таблице критических точек распределения 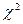 (Приложение 3) по заданному уровню значимости
(Приложение 3) по заданному уровню значимости 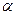 и числу степеней свободы k = s — 3 находят критическую точку
и числу степеней свободы k = s — 3 находят критическую точку 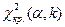 . Если
. Если 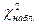 <
< 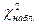 , то нет оснований отвергнуть гипотезу о нормальном распределении ГС. Если
, то нет оснований отвергнуть гипотезу о нормальном распределении ГС. Если 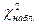 >
> 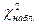 , то данную гипотезу отвергают.
, то данную гипотезу отвергают.
Интервальной называется оценка, которая определяется двумя числами - концами доверительного интервала, в котором с заданной доверительной вероятностью (близкой к единице) находится неизвестный оцениваемый параметр.
Среднее значение параметра а = М(Х) в ГС отличается от выборочного среднего 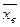 . Очевидно, что а может быть как больше, так и меньше
. Очевидно, что а может быть как больше, так и меньше 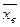 , т.е.
, т.е. 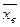 -
- 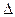 < а <
< а < 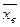 +
+ 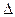 . Величина
. Величина 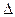 называется точностью оценки, а интервал
называется точностью оценки, а интервал
( 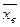 -
- 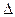 ;
; 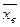 +
+ 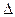 ) — доверительным интервалом. Для определения величины
) — доверительным интервалом. Для определения величины 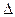 используется заданная вероятность
используется заданная вероятность 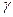 , близкая к единице, называемая доверительной вероятностью или надежностью интервальной оценки, с которой интервал (
, близкая к единице, называемая доверительной вероятностью или надежностью интервальной оценки, с которой интервал ( 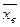 -
- 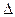 ;
; 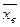 +
+ 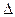 ) длины 2
) длины 2 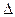 накрывает искомое значение параметра а.
накрывает искомое значение параметра а.
Если ГС подчиняется нормальному закону распределения (что встречается наиболее часто) и объем выборки достаточно велик (п > 30), то справедлива формула 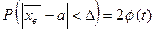 ,
,
где 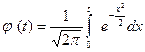 — функция Лапласа, t =
— функция Лапласа, t = 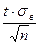 .
.
Ход работы
Приводятся результаты 40 наблюдений над двумерной случайной величиной (Х, У). Требуется для каждой случайной величины Х и У:
1. Проверить с помощью критерия согласия хи – квадрат Пирсона гипотезу о том, что выборка извлечена из генеральной совокупности с нормальным распределением (уровень значимости a = 0,05).
2. Найти интервальную оценку параметра а предполагаемого нормального распределения (доверительная вероятность g = 0,95).
Все вычисления проводить в Excel. Использовать результаты обработки статистических данных из лабораторной работы № 1.
Образец выполнения работы
Контрольные вопросы
1. Что называется эмпирическими частотами?
2. Что называется гипотезой?
3. Для чего используются критерии согласия?
4. Что называется уровнем значимости?
5. Назвать алгоритм применения критерии Пирсона?
6. Что называется интервальной оценкой?
7. Что называется точностью оценки?
8. Что называется доверительным интервалом?
Рекомендуемая литература
1. Красс М.С. Математика для экономических специальностей. – М: ИНФРА – М, 1998
2. Ермаков В.И. Общий курс высшей математики (для экономистов). – М: ИНФРА – М, 2001
3. Кремер Н.Ш. Высшая математика для экономистов. – М: ЮНИТИ - 2000
4. Данко П.Е. Высшая математика в упражнениях и задачах: Учебное пособие для вузов : В 2 ч. Ч 1,2 – М.: ОНИКС 21 век, 2003
5. Гмурман В.Е. Теория вероятностей и математическая статистика. – М.: Высшая школа, 1972
6. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике. – М.: Высшая школа, 1979
Лабораторная работа 3
«Корреляционный и регрессионный анализ»
Цель:Установление корреляционной зависимости между признаками Х и У.
Задачи:
· вычисление коэффициента корреляции;
· по таблице Чеддока оценить тесноту корреляционной связи;
· составить уравнения регрессии;
· построить линии регрессии на корреляционном поле.
Оборудование:компьютер.
