Б. Метод відносного руху суден

Покажемо, що цю задачу можна розв’язати, розглядаючи відносний рух суден.

Абсолютна швидкість 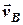будь-якої точки 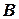(відносно нерухомої системи відліку) при складному русі визначається формулою

, (16)

де 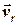– відносна швидкість точки 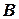в рухомій системі та – переносна швидкість точки за рахунок руху системи. Тоді для швидкості відносного руху точки 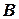отримуємо

. (17)

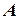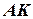Введемо рухому систему відліку , початок якої сумістимо з судном . У наступні моменти часу система буде рухатися зі швидкістю по траєкторії (рис. 4.1) абсолютного руху судна 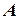. При цьому декартові вісі абсолютної 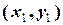та рухомої систем будуть залишатися паралельними ( та ). Тоді швидкість точки 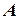буде відігравати роль переносної швидкості

. (18)

Отже, в системі судно 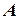буде залишатися нерухомим, а судно 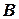буде рухатися з відносною швидкістю 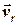, яку знаходимо з формули (17) з урахуванням (18)

. (19)

Спочатку розв’яжемо задачу графічно. За допомогою транспортира та лінійки будуємо початкове положення суден 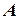та 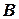. Оберемо зручний для швидкостей масштаб, наприклад, 1 см = 2 вузла та побудуємо вектори абсолютних швидкостей суден та 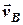(рис. 4.3). Щоб графічно побудувати вектор відносної швидкості 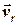треба згідно (19) до вектора 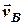додати вектор ( ) (рис. 4.3).

Траєкторія руху судна В відносно нерухомого судна А лежить на векторі 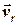і визначає лінію відносного руху . Положення цієї лінії свідчить про те, що в нашому випадку судно В пройде перед судном судна А (по носу).

Для того, щоб знайти найкоротшу відстань між суднами, треба з точки А опустити перпендикуляр на лінію відносного руху – так ми отримуємо точку С. Вимірюємо мінімальну відстань між суднами d_кр = = 2,1 милі.

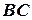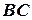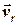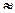Щоб визначити час розходження, потрібно відстань (вимірювання дає ≈ 9,1 миль) поділити на швидкість відносного руху. Вимірюємо довжину вектора та знаходимо модуль відносної швидкості = 19,5 вузлів. Отже = 9,1/19,5 ≈ 0,47 годин 28 хв.

Щоб розв’язати задачу аналітично,запишемо вирази для векторів швидкостей суден. Оскільки декартові вісі рухомої та абсолютної систем лишаються паралельними, то:

= , (20)

= . (21)

Тоді для вектора відносної швидкості отримуємо

+ (22)

Зауважимо, що отримані раніше вирази (9) та (10) для величин 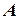та визначають компоненти відносної швидкості та , відповідно. Після цього підрахуємо модуль відносної швидкості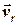

= 19,4 (вуз.). (23)

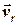Рівняння лінії відносного руху можна записати як рівняння прямої, що проходить через точку вздовж вектора , тому воно має вигляд

, (24)

де = 8,30 (милі) та = 4,41 (милі) та – тангенс кута нахилу лінії відносного руху до осі x, який знаходимо через компоненти вектора відносного руху

. (25)

Найкоротша відстань між суднами визначиться віддаллю точки А(0,0) від цієї прямої, тому

. (26)

Зауважимо, що формула (26) співпадає з формулою (15). Підставляючи дані, отримуємо

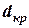= 2,00 (милі).

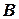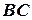Для знаходження моменту часу, коли судно буде в точці , потрібно віддаль поділити на модуль відносної швидкості

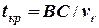. (27)

Величину 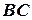розраховуємо їз прямокутного трикутника

= 9,18 милі,

тоді

годин » 28 хв.

Таким чином усіма методами ми отримали близькі результати, які вказують, що швидкість відносного зближення суден = 19,4 вузла, вони розійдуться через 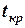» 28 хв. на найкоротшій відстані 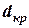= 2,0 милі.

Більш того, розв’язок задачі методомвідносного руху суден, дозволяє узагальнити задачу на випадок розходження суден в області дії постійної течії, бо відносна швидкість в цьому випадку не зміниться. Дійсно

. (28)

Відповідь: 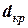= 2,00 милі та 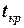= 28 хв.