Вращение твёрдого тела вокруг неподвижной оси
Вращением твёрдого тела вокруг неподвижной оси называется такое его движение, при котором две точки тела остаются неподвижными в течение всего времени движения.
При этом также остаются неподвижными все точки тела, расположенные на прямой, проходящей через его неподвижные точки. Эта прямая называется осью вращения тела.
 Пусть точки A и B неподвижны. Вдоль оси вращения направим ось
Пусть точки A и B неподвижны. Вдоль оси вращения направим ось  . Через ось вращения проведём неподвижную плоскость
. Через ось вращения проведём неподвижную плоскость 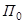 и подвижную
и подвижную 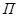 , скреплённую с вращающимся телом (при
, скреплённую с вращающимся телом (при 
 ).
).
Положение плоскости 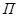 и самого тела определяется двугранным углом между плоскостями
и самого тела определяется двугранным углом между плоскостями 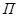 и
и 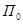 . Обозначим его
. Обозначим его  . Угол
. Угол  называется углом поворота тела.
называется углом поворота тела.
Положение тела относительно выбранной системы отсчета однозначно определяется в любой момент времени, если задано уравнение 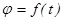 , где
, где 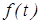 - любая дважды дифференцируемая функция времени. Это уравнение называется уравнением вращения твёрдого тела вокруг неподвижной оси. У тела, совершающего вращение вокруг неподвижной оси, одна степень свободы, так как его положение определяется заданием только одного параметра – угла
- любая дважды дифференцируемая функция времени. Это уравнение называется уравнением вращения твёрдого тела вокруг неподвижной оси. У тела, совершающего вращение вокруг неподвижной оси, одна степень свободы, так как его положение определяется заданием только одного параметра – угла  .
.
Угол  считается положительным, если он откладывается против часовой стрелки глядя с конца оси, и отрицательным – в противоположном направлении. Траектории точек тела при его вращении вокруг неподвижной оси являются окружностями, расположенными в плоскостях перпендикулярных оси вращения.
считается положительным, если он откладывается против часовой стрелки глядя с конца оси, и отрицательным – в противоположном направлении. Траектории точек тела при его вращении вокруг неподвижной оси являются окружностями, расположенными в плоскостях перпендикулярных оси вращения.
Для характеристики вращательного движения твердого тела вокруг неподвижной оси введём понятия угловой скорости и углового ускорения.
Алгебраической угловой скоростью тела в какой-либо момент времени называется первая производная по времени от угла поворота в этот момент, то есть  .
.
Угловая скорость является положительной величиной при вращении тела против часовой стрелки, так как угол поворота возрастает с течением времени, и отрицательной – при вращении тела по часовой стрелке, потому что угол поворота при этом убывает.
Размерность угловой скорости по определению: 
Алгебраическим угловым ускорением тела называется первая производная по времени от угловой скорости, то есть вторая производная от угла поворота т.е. 
Размерность углового ускорения по определению: 
Введем понятия векторов угловой скорости и углового ускорения тела.
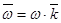 и
и 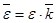 , где
, где 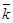 - единичный вектор оси вращения. Векторы
- единичный вектор оси вращения. Векторы  и
и 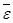 можно изображать в любых точках оси вращения, они являются скользящими векторами.
можно изображать в любых точках оси вращения, они являются скользящими векторами.

Алгебраическая угловая скорость это проекция вектора угловой скорости на ось вращения. Алгебраическое угловое ускорение это проекция вектора углового ускорения скорости на ось вращения.
Если 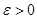 при
при 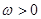 , то алгебраическая угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов
, то алгебраическая угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов  и
и 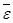 совпадают, оба они направлены в положительную сторону оси вращения
совпадают, оба они направлены в положительную сторону оси вращения 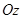 .
.
При  и
и 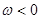 тело вращается ускоренно в отрицательную сторону. Направление векторов
тело вращается ускоренно в отрицательную сторону. Направление векторов  и
и 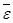 совпадают, оба они направлены в отрицательную сторону оси вращения
совпадают, оба они направлены в отрицательную сторону оси вращения 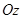 .
.
Если  при
при 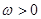 , то имеем замедленное вращение в положительную сторону. Векторы
, то имеем замедленное вращение в положительную сторону. Векторы  и
и 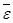 направлены в противоположные стороны.
направлены в противоположные стороны.
Если 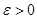 при
при 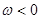 , то имеем замедленное вращение в отрицательную сторону. Векторы
, то имеем замедленное вращение в отрицательную сторону. Векторы  и
и 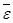 направлены в противоположные стороны.
направлены в противоположные стороны.
Угловую скорость и угловое ускорение на рисунках часто изображают дуговыми стрелками вокруг оси вращения. Дуговая стрелка для угловой скорости указывает направление вращения тела, а дуговая стрелка для углового ускорения – направление, в котором увеличивается алгебраическая угловая скорость. Для ускоренного вращения дуговые стрелки для угловой скорости и углового ускорения имеют одинаковые направления, для замедленного их направления противоположны.
