Задачи для самостоятельного решения. а) Написать уравнение прямой и привести его к общему виду, если

а) Написать уравнение прямой и привести его к общему виду, если

1) прямая проходит через точку М(-1, 2) перепендикулярно вектору

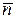= (2, -3);

2) прямая проходит через точку М(-1, 1) параллельно вектору

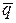= (2, 0);

3) прямая проходит через точки М₁(1, 2) и М₂(-1, 0).

б) Составить уравнение прямой, которая проходит через точку М(8, 6) и отсекает от координатного угла треугольник с площадью, равной 12 кв. ед.

Нормальное уравнение прямой. Расстояние от точки до прямой

Если общее уравнение прямой (8.1) умножить на

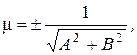
где знак выбирается из условия mС<0, то получим уравнение

ах + bу - р = 0, (8.11)

где коэффициенты имеют следующий геометрический смысл: а = cos a,

b= sin a, a - угол между нормалью к прямой и осью Ох, р - расстояние от прямой до начала координат. Уравнение (8.11) называется нормальным уравнением прямой.

Пример. Найдем расстояние от начала координат до прямой

12х - 5у -65 = 0.

Приведем уравнение прямой к нормальному виду, домножив его на

m = 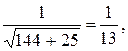где знак “плюс” выбран так, как С = -65. Тогда имеем (12/13)х - (5/13)у - 5 = 0, следовательно, нужное нам расстояние равно р = 5.

Расстояние от точки (х₀, у₀) до прямой (8.1) вычисляется по формуле:

d = 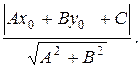(8.12)

Пример. Определим расстояние от точки (1, 2) до прямой

20х -21у -58 = 0.

Из формулы (8.12) получаем

d = .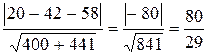

Если прямые А₁х +В₁у + С₁ = 0 и А₂х + В₂у + С₂ = 0 пересекаются, то их точку пересечения можно найти, решая систему:

.

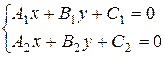Пример. Покажем, что прямые 3х - 2у + 1= 0 и 2х + 5у -12 = 0 пересекаются, и найдем точку пересечения.

Составим систему и решим ее. Полученная точка и является точкой пересечения:

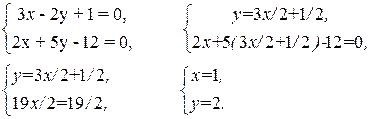
Итак, (1,2)- искомая точка пересечения прямых.

Геометрические задачи с использованием различных

Уравнений прямой

В различных геометрических задачах используются те или иные уравнения прямой в зависимости от условий. При этом важно помнить геометрический смысл различных коэффициентов в уравнении прямой. Наиболее часто используются следующие два факта: в общем уравнении прямой (8.1) коэффициенты при неизвестных образуют вектор 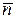= (А, В), ортогональный к этой прямой (вектор нормали); в уравнении

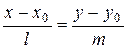
вектор 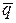= (l, m) параллелен этой прямой (направляющий вектор), а прямая проходит через точку (х₀, у₀).

Примеры.

а) Составим уравнение прямой, проходящей через точку (-2, -5), и параллельной прямой 3х + 5у + 2 = 0.

Из уравнения (8.8) имеем А(х+2)+В(у+5)=0. Из условия параллельности прямых заключаем, что ортогональные им вектора 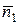= (3, 5) и 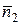= (А, В) также параллельны. Следовательно, можно положить 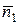= = 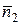(3, 5) (длина вектора нормали не имеет значения). Итак, нужная нам прямая имеет уравнение:

3(х + 2) + 5(у + 5) = 0 или 3х + 5у + 31 = 0.

б) Даны вершины треугольника А(2, 2), В(-2, -8), С(-6, -2). Составим уравнение медиан треугольника.

Медиана проходит через вершину А и делит отрезок ВС пополам. Определим координаты середины отрезка ВС: х₀ = ((-2) + (-6))/2 = -4,

у₀ = ((-8) + (-2))/2 = -5. Пользуясь теперь уравнением прямой (8.10), проходящей через две точки, получаем уравнение медианы, проходящей через вершину А: (х + 4)/6 = (у + 5)/7 или 7х - 6у - 2 = 0.

Аналогично находим урвнения остальных медиан:

х₁ = 0, у₁ = -3, (х + 6)/6 = (у + 2)/(-1), х + 6у + 18 = 0,

х₂ = -2, у₂ = 0, (х + 2)/0 = (у + 8)/8, х + 2 = 0.

в) Даны вершины треугольника А(0, 1), В(12, -1), С(6, 5). Составим уравнение высоты треугольника, проведенной из вершины С.

Высота проходит через точку С, следовательно, ее уравнение можно записать в виде К(х - 6) + М(у - 5) = 0. Найдем координаты вектора нормали (К, М): так как наша прямая ортогональна стороне АВ треугольника АВС, то вектор, соединяющий точки А и В, является ортогональным прямой, его и можно взять в качестве вектора-нормали: (12 - 0, -1 - 1) = (12, -2). Итак, уравнение прямой имеет вид: 12(х - 6) - 2(у - 5) = 0 или 12х - 2у -62 = 0.