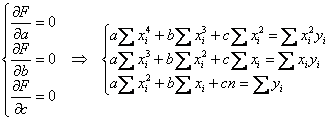Пермский национальный исследовательский политехнический университет.

Доклад

По дисциплине «Теория вероятностей и математическая статистика »

На тему: «Метод наименьших квадратов».

Выполнила: студентка Гуманитарного

факультета очного отделения

Специальность: Социология и политология

Группа: С-15-1б

Иняткина Анна

Пермь 2015

Метод наименьших квадратов (МНК) – один из наиболее широко используемых методов при решении многих задач восстановления регрессионных зависимостей. Впервые МНК был использован Лежандром в 1806 г. для решения задач небесной механики на основе экспериментальных данных астрономических наблюдений. В 1809 г. Гаусс изложил статистическую интерпретацию МНК и тем самым дал начало широкого применения статистических методов при решении задач восстановления регрессионных зависимостей. Строгое математическое обоснование и установление границ содержательной применимости метода наименьших квадратов даны А.А. Марковым и А.Н. Колмогоровым. Ныне способ представляет собой один из важнейших разделов математической статистики и широко используется для статистических выводов в различных областях науки и техники.

Метод наименьших квадратов — один из методов регрессионного анализа для оценки неизвестных величин по результатам измерений, содержащих случайные ошибки, или иными словами статистический прием, с помощью которого неизвестные параметры модели оцениваются путем минимизации суммы квадратов отклонений действительных (эмпирических) значений от теоретических.

Он может использоваться для «решения» переопределенных систем уравнений (когда количество уравнений превышает количество неизвестных), для поиска решения в случае обычных (не переопределенных) нелинейных систем уравнений, для аппроксимации точечных значений некоторой функции. МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров регрессионных моделей по выборочным данным.

Применяется также для приближённого представления заданной функции другими (более простыми) функциями и часто оказывается полезным при обработке наблюдений. В настоящее время широко применяется при обработке количественных результатов различных опытов, измерений.

При обработке результатов измерений часто возникает необходимость построить эмпирическую формулу, дающую аналитическое выражение функциональной зависимости, заданной таблицей.

Общепринятым и весьма эффективным при решении подобных задач является так называемый как раз наш метод наименьших квадратов, при котором требование наилучшего согласования искомой кривой U = f(x) и экспериментальных точек сводятся к тому, чтобы «сумма квадратов отклонений» экспериментальных точек от искомой функции U = f(x, а, b, …) обращалась в минимум.

«Метод наименьших квадратов» имеет перед другими методами приближения существенные преимущества:

ü он приводит к сравнительно простому математическому способу определения параметров а, b, с, … искомого функционала;

ü он дает довольно веское теоретическое обоснование с вероятностной точки зрения.

Основным недостатком МНК является чувствительность оценок к резким выбросам, которые встречаются в исходных данных.

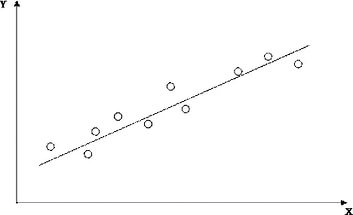
Пример прямой, построенной в диапазоне фактических точек.

Пусть в некоторой предметной области исследуются показатели 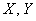, которые имеют количественное выражение. При этом есть все основания полагать, что показатель 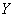зависит от показателя 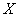. Это полагание может быть как научной гипотезой, так и основываться на элементарном здравом смысле.

Связь между элементами может быть сильной и слабой, прямой и обратной.

Приведём в пример продовольственные магазины. Обозначим через:

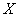– торговую площадь продовольственного магазина, кв.м.,
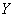– годовой товарооборот продовольственного магазина, млн. руб.

Ведь обычно, чем больше площадь магазина, тем в большинстве случаев будет больше его товарооборот.

Предположим, что после проведения 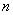наблюдений/опытов/подсчётов в нашем распоряжении оказываются числовые данные:

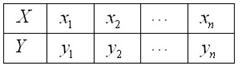
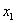– это площадь 1-го магазина, 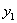– его годовой товарооборот, 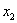– площадь 2-го магазина, 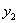– его годовой товарооборот и т.д.

Табличные данные также можно записать в виде точек 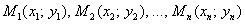и изобразить в декартовой системе .

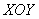Возникает важный вопрос: сколько точек нужно для качественного исследования?

Чем больше, тем лучше. Минимально допустимый набор состоит из 5-6 точек. Кроме того, при небольшом количестве данных в выборку нельзя включать «аномальные» результаты. Так, например, небольшой элитный магазин может выручать на порядки больше «своих коллег», искажая тем самым общую закономерность, которую и требуется найти.

Иными словами нам нужно подобрать функцию 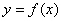, график которой проходит как можно ближе к точкам 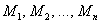. Такую функцию называют аппроксимирующей(аппроксимация – приближение) или теоретической функцией.

Таким образом, разыскиваемая функция должна быть достаточно проста и в то же время отражать зависимость адекватно. Один из методов нахождения таких функций и называется методом наименьших квадратов. Пусть некоторая функция 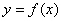приближает экспериментальные данные :

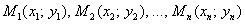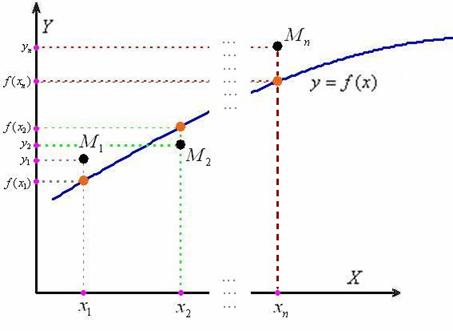
Как оценить точность данного приближения? Вычислим 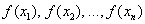и разности (отклонения) 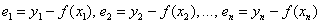между экспериментальными и функциональными значениями.

Первая мысль, которая приходит в голову – это оценить, насколько велика сумма 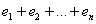, но проблема состоит в том, что разности могут быть и отрицательны (например, 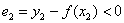) и отклонения в результате такого суммирования будут взаимоуничтожаться.

Решаем через метод наименьших квадратов, в котором возможные отрицательные значения ликвидируются не модулем, а возведением отклонений в квадрат:

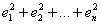, после чего усилия направлены на подбор такой функции 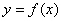, чтобы сумма квадратов отклонений 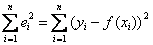была как можно меньше. Собственно, отсюда и название метода.

Возвратимся к другому важному моменту: как отмечалось выше, подбираемая функция должна быть достаточно проста – но ведь и таких функций тоже немало: линейная,гиперболическая,экспоненциальная,логарифмическая,квадратичная и т.д. Какой класс функций выбрать для исследования? Простой, но эффективный приём:

– Проще всего изобразить точки 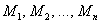на чертеже и проанализировать их расположение. Если они имеют тенденцию располагаться по прямой, то следует искать уравнение прямой 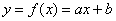с оптимальными значениями 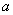и . И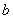ными словами, задача состоит в нахождении таких коэффициентов 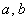– чтобы сумма квадратов отклонений 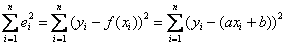была наименьшей.

Если же точки расположены, например, по гиперболе, то заведомо понятно, что линейная функция будет давать плохое приближение. В этом случае ищем наиболее подходящие коэффициенты 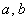для уравнения гиперболы 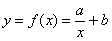– те, которые дают минимальную сумму квадратов .

А теперь обратитим внимание, что в обоих случаях речь идёт о функции двух переменных, аргументами которой являются параметры разыскиваемых зависимостей:

И по существу нам требуется решить стандартную задачу – найти минимум функции двух переменных.

Продолжим рассматривать наш пример: предположим, что «магазинные» точки 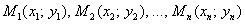имеют тенденцию располагаться по прямой линии и есть все основания полагать наличие линейной зависимости 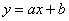товарооборота от торговой площади. Найдём ТАКИЕ коэффициенты а и б, чтобы сумма квадратов отклонений 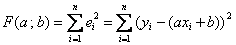была наименьшей.

При минимизации функции неизвестными являются значения коэффициентов регрессии a и b. Значения зависимой и независимой переменных известны из наблюдений.

Для того чтобы найти минимум функции двух переменных, нужно вычислить частные производные этой функции по каждой из оцениваемых параметров и приравнять их к нулю. В результате мы получим стационарную систему уравнений для нашей функции.

(Согласно правилу линейности дифференцировать можно прямо под значком суммы):

Составим стандартную систему:

Сокращаем каждое уравнение на 2 и, кроме того, разбиваем суммы:

Перепишем систему в прикладном виде:

Координаты точек 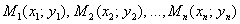нам известны.. Суммы 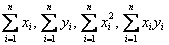мы можем найти. Составляем простейшую систему двух линейных уравнений с двумя неизвестными (а и b). Систему решаем, например,методом Крамера, в результате чего получаем стационарную точку 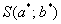. Проверяя достаточное условие экстремума, можно убедиться, что в данной точке функция 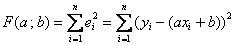достигает именно минимума.

Функция 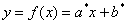наилучшим образом (по крайне мере, по сравнению с любой другой линейной функцией) приближает экспериментальные точки 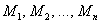. иначе говоря, её график проходит максимально близко к этим точкам. В традициях эконометрикиполученную аппроксимирующую функцию также называют уравнением парной линейной регрессии.

Рассматриваемая задача имеет большое практическое значение. В ситуации с нашим примером, уравнение 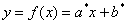позволяет прогнозировать, какой товарооборот(«игрек») будет у магазина при том или ином значении торговой площади (том или ином значении «икс»). Да, полученный прогноз будет лишь прогнозом, но во многих случаях он окажется достаточно точным.

Пример:

В результате исследования взаимосвязи двух показателей, получены следующие пары чисел:

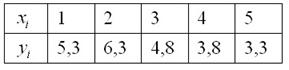
Методом наименьших квадратов найти линейную функцию, которая наилучшим образом приближает эмпирические (опытные) данные. Сделать чертеж, на котором в декартовой прямоугольной системе координат построить экспериментальные точки 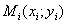и график аппроксимирующей функции 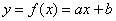. Найти сумму квадратов отклонений между эмпирическими 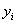и теоретическими 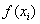значениями.

Коэффициенты 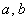оптимальной функции 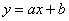найдём как решение системы:

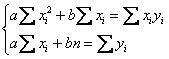
В целях более компактной записи переменную-«счётчик» можно опустить, поскольку и так понятно, что суммирование осуществляется от 1 до .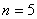

Расчёт нужных сумм удобнее оформить в табличном виде:

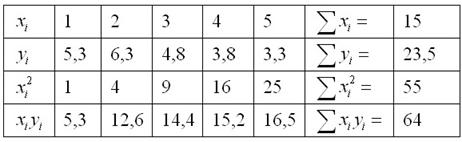
Таким образом, получаем следующую систему:
Решим методом Крамера:
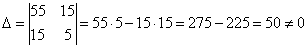, значит, система имеет единственное решение.

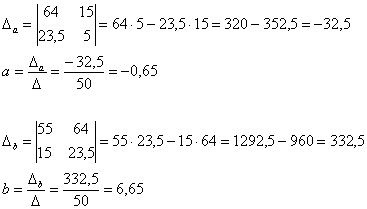
Выполним проверку. Подставим найденное решение 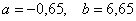в левую часть каждого уравнения системы:

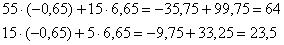
Получены правые части соответствующих уравнений, значит, система решена правильно.

Таким образом, искомая аппроксимирующая функция: 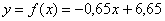из всех линейных функций экспериментальные данные наилучшим образом приближает именно она.

В отличие от прямой зависимости товарооборота магазина от его площади, найденная зависимость является обратной (принцип «чем больше – тем меньше»), и этот факт сразу выявляется по отрицательному угловому коэффициенту. Функция 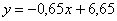сообщает нам о том, что с увеличение некоего показателя 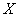на 1 единицу значение зависимого показателя 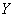уменьшается в среднемна 0,65 единиц. К примеру, чем выше цена на гречку, тем меньше её продано.

Для построения графика аппроксимирующей функции найдём два её значения:

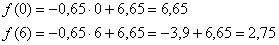
и выполним чертёж:

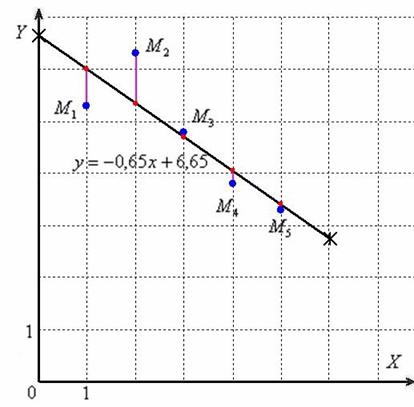
Построенная прямая называется линией тренда (а именно – линией линейного тренда, т.е. в общем случае тренд – это не обязательно прямая линия).

Вычислим сумму квадратов отклонений 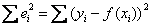между эмпирическими 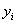и теоретическими 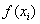значениями. Геометрически – это сумма квадратов длин отрезков между теоретическими и экспериментальными точками.

Вычисления сведём в таблицу:

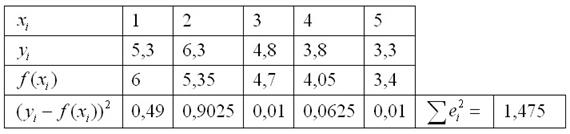
Их можно опять же провести вручную, на всякий случай приведу пример для 1-й точки:

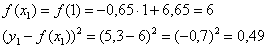
В заключение доклада краткая информация о нахождение зависимостей некоторых других видов. Собственно, и рассказывать-то особо нечего, поскольку принципиальный подход и алгоритм решения остаются прежними.

Предположим, что расположение экспериментальных точек 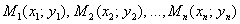напоминает гиперболу. Тогда чтобы отыскать коэффициенты 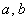наилучшей гиперболы 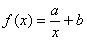, нужно найти минимум функции 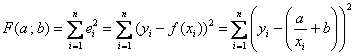подробные вычисления и приводят к похожей системе:

Если есть все основания полагать, что точки 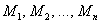располагаются по логарифмической кривой 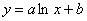, то для розыска оптимальных значени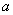й и 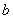находим минимум функции 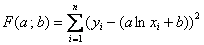. Формально в системе (*) нужно заменить 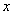на :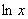

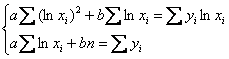
С экспоненциальной зависимостью 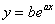ситуация чуть сложнее. Чтобы свести дело к линейному случаю, прологарифмируем функцию и воспользуемся свойствам логарифма:

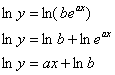
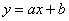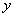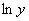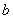Теперь, сопоставляя полученную функцию с линейной функцией , приходим к выводу, что в системе (*) нужно заменить на , а – на 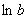. Для удобства обозначим :

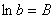Обращаем внимание, что система разрешается относительно 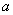и 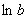, и поэтому после нахождения корней нужно не забыть найти сам коэффициент .

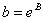Чтобы приблизить экспериментальные точки 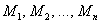оптимальной параболой 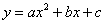, следует найти минимум функции трёх переменных 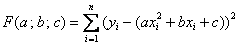. После осуществления стандартных действий получаем следующую «рабочую» систему: