Глава 2. тепловое расширение твердых и жидких тел 4 страница

а) Прочитав условие задачи, нужно ясно представить, какой газ участвует в том или ином процессе, и убедиться, что при изменении параметров состояния газа его масса не меняется.

б) Сделать, если это возможно, схематический чертеж и, отметив каждое состояние газа, указать параметры р, V, Т, характеризующие эти состояния. Определить из условия задачи, какой из этих трех параметров не меняется, и какому газовому закону подчиняются переменные параметры.

В общем случае могут изменяться все три параметра р, V и Т.

в) Записать уравнение объединенного газового закона Клапейрона для данных двух состояний. Если какой-либо параметр остается неизменным, уравнение автоматически переходит в одно из трех уравнений: закон Бойля — Мариотта, Гей-Люссака или Шарля.

В тех случаях, когда газ заключен в цилиндрический сосуд и объем газа меняется только за счет изменения высоты его столба, но не сечения, уравнение Клапейрона нужно сразу записывать в виде:

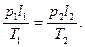
г) Представить в развернутом виде параметры P₁, V₁, P₂, р2, V₂ выразив их через заданные величины. Вполне естественно, что расшифровывать нужно только те параметры, которые заданы косвенно, но не те, что даны явно. Особое внимание здесь следует обратить на определение давления. Чтобы его найти, часто приходится использовать закон Паскаля: провести нулевой уровень через границу, отделяющую газ от жидкости, и записать уравнение равновесия жидкости.

д) Записать математически все вспомогательные условия и решить полученную систему уравнений относительно неизвестной величины.

Если в задаче рассматривают процессы, связанные с изменением состояния двух или трех газов, отделенных друг от друга поршнями или входящих в состав смеси, то все указанные действия нужно проделать для каждого газа отдельно.

В задачах на газовые законы рекомендуется пользоваться только абсолютной температурой и сразу же переводить значения температуры по шкале Цельсия в значения по шкале Кельвина.

3. Если по условию задачи дано только одно состояние газа и требуется определить какой-либо параметр этого состояния или же даны два состояния с разной массой газа, то рекомендуется поступать так:

а) Установить, какие газы участвуют в рассматриваемых процессах.

б) Для каждого состояния каждого газа (если их несколько) составить уравнение Менделеева – Клапейрона. Если дана смесь газов, то это уравнение записывают для каждого компонента. Связь между значениями давлений отдельных газов и результирующим давлением смеси устанавливается законом Дальтона.

в) Записать математически дополнительные условия задачи и решить полученную систему уравнений относительно искомой величины.

В комбинированных задачах, где рассматривается движение сосуда с газом, уравнение газового состояния добавляют к уравнениям механики.

Пример 1.Для погружения и всплытия подводной лодки в ней имеются два сообщающихся между собой резервуара. В погруженном состоянии один из резервуаров емкостью V заполнен водой, во втором, емкостью V₁, находится сжатый воздух. Каково должно быть минимальное давление сжатого воздуха, чтобы при всплытии лодки с глубины Н сжатый воздух полностью вытеснил воду из балластной цистерны? Атмосферное давление нормальное, изменением температуры воздуха при расширении пренебречь.

Решение. Если соединить резервуары между собой, то при достаточной степени сжатия воздух, заключенный во втором сосуде, начнет расширяться и вытеснит воду из балластной цистерны наружу. Так как по условию задачи масса и температура сжатого воздуха не меняются, то увеличение его объема вызовет понижение давления. Учитывая сделанные выше рекомендации, решение задачи следует построить на законе Бойля — Мариотта.

Пусть P_l и V₁ – давление и объем сжатого воздуха до расширения, P₂ и V₂ – давление и объем воздуха в тот момент, когда он, вытеснив воду, займет оба резервуара, тогда

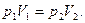
Обратимся теперь к каждому из параметров и посмотрим, какие из них нужно представить в развернутом виде. Давление P_l требуется определить по условию задачи, объем V₁ задан — он равен объему резервуара со сжатым воздухом, давление P₂ можно найти, исходя из следующего. Чтобы вытеснить воду из балластного резервуара, воздух во втором состоянии должен находиться под давлением, большим или равным гидростатическому давлению на глубине Н, т. е.

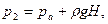
где ρ – плотность морской воды. Остается выразить объем V₂, он, как нетрудно заметить, равен суммарной емкости обоих резервуаров:

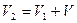
Подставляя выражения для P₂ и V₂ в формулу закона Бойля — Мариотта, мы получим уравнение газового состояния в окончательном виде:

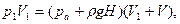
откуда начальное давление в резервуаре со сжатым воздухом

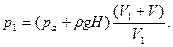
Пример 2. Посредине откачанной и запаянной с обоих концов горизонтальной трубки находится столбик ртути длиной h=19.6 мм. Если трубку поставить под углом a=30° к горизонту, то столбик ртути переместится на ∆l₁=20 мм; если поставить вертикально — на ∆l₂=30 мм. До какого давления откачан воздух из трубки?

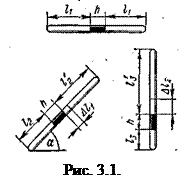Решение. В задаче говорится о трех состояниях двух газов одинаковой массы, разделенных столбиком ртути (рис.3.1). В процессе перемещения трубки из горизонтального положения в вертикальное, вследствие смещения столбика ртути, газ, находящийся в правой части трубки будет расширяться, в левой — сжиматься.

Так как по условию задачи масса и температура не меняются, то для каждой пары состояний каждого газа должно иметь место уравнение закона Бойля – Мариотта. Совокупность этих уравнений полностью характеризует изотермический процесс, описываемый в данной задаче.

Состояние газа при горизонтальном положении трубки примем за первое состояние. Вторым состоянием будем считать состояние газа в наклонной трубке, третьим — состояние газа при вертикальном положении трубки.

Обозначим давление газа в левой части трубки в каждом из этих состояний через p_l, p₂, p₃, длину столбов воздуха через l_l, l₂, l₃, тогда, применяя закон Бойля – Мариотта для каждой пары состояний и учитывая, что площадь поперечного сечения трубки всюду одинакова, получим:

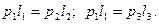
Аналогично для газа, заключенного в правой части трубки:

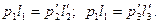
так как в первом состоянии давления и объемы газа в обеих частях трубки были одинаковы.

Если при отклонении трубки от горизонтального положения на угол α столбик ртути сместится на расстояние Δl₁ ( при отклонении на угол 90°— на расстояние Δl₂, то, как видно из чертежа,

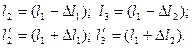
Кроме того, при равновесии столбика ртути должно быть

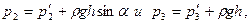
где ρ – плотность ртути.

Подставляя в уравнения закона Бойля — Мариотта вместо l₂, l₃, 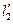, , 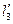p₂ и p₃ их выражения, получим:

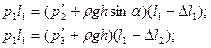
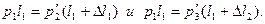
Решая полученные уравнения относительно p_l, найдем:

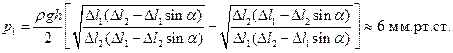
Пример 3.В стеклянную манометрическую трубку, запаянную с одного конца, налита ртуть. Высота столба воздуха в запаянном колене равна 2Н, причем уровень - ртути в открытом колене стоит на Н выше, чем в закрытом. Манометр установлен в ракете, которая начинает подниматься вертикально вверх с ускорением а=g. Какова будет разность уровней ртути в коленах манометра при подъеме ракеты, если в кабине ракеты поддерживается нормальное атмосферное давление?

Решение. При ускоренном движении тел в вертикальном направлении на эти тела со стороны опоры действует сила нормального давления, сообщающая им ускорение g + а. Такая же по величине, но противоположная по направлению сила действует и на опору со стороны расположенных на ней тел. Эффект получается такой, как если бы ускорение свободного падения g возросло на величину а. В результате вес тел, а следовательно, и удельный вес в движущейся системе возрастает и становится равным не pg, a Р (g + a).

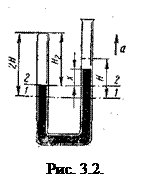
Аналогичное явление происходит и при подъеме манометра в ракете. Перед стартом ракеты воздух в закрытом колене манометра был сжат до такой степени, что уравновешивал атмосферное давление и давление столбика ртути в открытом колене. Как только ракета начнет подниматься вверх с ускорением а, давление столба ртути на поверхность 1–1 (рис. 3.2) возрастет, ртуть начнет переливаться в закрытое колено, сжимая находящийся там воздух. Разность уровней ртути будет уменьшаться до тех пор, пока упругость воздуха не достигнет величины, необходимой для равновесия.

Таким образом, при ускоренном движении ракеты происходит изотермическое сжатие воздуха в закрытом колене, вызванное увеличением удельного веса ртути.

Так как в процессе сжатия температура и масса воздуха остаются неизменными, то в этом случае справедлив закон Бойля – Мариотта.

Если в неподвижной ракете давление и высота столба воздуха в закрытом колене были равны р₁ и 2H, а при ускоренном подъеме – р₂ и H2, то

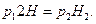
По условию задачи исходная высота воздушного столба задана, поэтому дальнейшее решение задачи состоит в том, чтобы представить в развернутом виде p₁и р₂.

Выбрав поверхность нулевого уровня по границе 1–1, согласно закону Паскаля запишем:

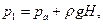
где р_а – атмосферное давление; Н – разность уровней ртути в сосудах в неподвижной ракете; ρg – удельный вес ртути.

Выбирая поверхность одного уровня по границе 2–2 для каких-нибудь двух произвольных точек, лежащих на этой поверхности, при относительном равновесии жидкости в сосудах будем иметь:

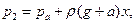
где р (g + а) — удельный вес ртути, поднимающейся вертикально вверх с ускорением а; х– разность уровней ртути в сосудах во время движения ракеты.

Высоту столба воздуха во втором состоянии можно выразить через ее начальное значение 2H, начальную разность уровней ртути H и конечную разность x. Как видно из чертежа,

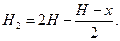
(Второй член правой части равенства численно равен смещению уровней ртути от начального положения.)

Подставив выражения для p_l, р₂ и H₂ в формулу закона Бойля – Мариотта, мы и получим окончательное уравнение для определения неизвестной величины х:

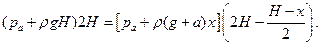
Или, если учесть, что р_а=pgH₀ и а=g, после сокращений получим:

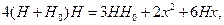
откуда

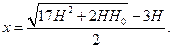
Пример 4.Компрессор захватывает при каждом качании воздух объемом V_к=1 л при нормальном атмосферном давлении и температуре Т₁=273 К и нагнетает его в автомобильный баллон,· объем которого V=0.5 м³; температура воздуха в баллоне Т₂=290 К. Сколько качаний должен сделать компрессор, чтобы площадь соприкосновения покрышки с полотном дороги уменьшилась на ΔS =100 см², если до этого она равнялась S =450 см² и на колесо приходится нагрузка в F=4.9 кн?

Решение. В процессе работы компрессора воздух, нагнетаемый в баллон, сжимается от объема, занимаемого им в атмосфере, до объема в автопокрышке. В результате упругость баллона возрастает и площадь его соприкосновения с дорогой уменьшается. Следует заметить, что в баллоне и до этого мог находиться воздух, именно поэтому в условиях задачи и говорится об уменьшении площади соприкосновения покрышки с дорогой, вызванном увеличением давления, но не о самой площади соприкосновения, величина которой, помимо прочего, зависит от полного давления в баллоне.

Так как при переходе воздуха из свободного состояния в сжатое изменяются его давление, объем и температура, то основным уравнением, характеризующим процесс, служит уравнение объединенного газового закона Клапейрона.

В первом состоянии (в атмосфере) параметры состояния воздуха равны соответственно p_l, V₁, T₁. Во втором состоянии (в баллоне) этот же воздух после n качаний компрессора будет сжат до давления p₂, займет объем баллона V₂ и нагреется до температуры Т₂. Объем баллона считается при этом неизменным. Параметры первого и второго состояний воздуха связаны между собой уравнением

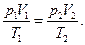
По условию задачи нам даны p_l = р₀, V₂= V₁, T₁ и T₂, поэтому нужно расшифровать V₁ и p₂.

Если при одном качании компрессор захватывает воздух в объеме V_к, то весь воздух, содержащийся в объеме V₁ ( будет перекачан из атмосферы в баллон за n качаний, т. е.

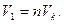
Чтобы определить давление р₂, нужно учесть следующее. Если до того, как автопокрышку стали накачивать, в ней было создано начальное избыточное давление р_и и площадь соприкосновения покрышки с дорогой равнялась S, то

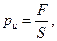
где F – нагрузка, приходящаяся на колесо. После того как баллон подкачали, избыточное давление в нем возросло на p₂ и стало равным р_и + р₂; площадь соприкосновения с полотном дороги уменьшилась на ΔS и стала равной S–ΔS. Так как нагрузка на колесо осталась прежней, то

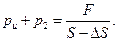
Исключая из последних двух равенств начальное давление р_и и подставляя в исходное уравнение вместо параметров V₁ и р₂ их выражения, мы получим уравнение объединенного газового закона в окончательном виде:

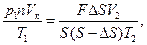
откуда

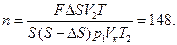
Пример 5. Поршни двух одинаковых цилиндров связаны между собой жесткой тягой так, что объемы под поршнями равны. Под поршнями находится одинаковое количество газа при температуре Т₀. Каково будет давление в цилиндрах, если один из них нагреть до температуры Т₁, а второй охладить до температуры Т₂ Чему будет равно при этом относительное изменение объема газа в каждом цилиндре? Весом поршней и тяги пренебречь, трение не учитывать, атмосферное давление р_а.

Решение. В задаче рассматривают два состояния двух одинаковых газов, заключенных в разные цилиндры (рис. 3.3). Поршни этих цилиндров связаны между собой жесткой тягой и могут скользить без трения. В такой системе изменение давления или объема одного из газов вызывает изменение параметров 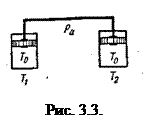состояния другого газа. Причем изменения объемов газа под поршнями будут всегда равны между собой, так как по условию задачи сами цилиндры и объемы под поршнями одинаковые, а поршни связаны друг с другом жестко. Что касается давлений газов, то они могут быть разными. На них накладывается лишь единственное ограничение: в сумме эти давления должны уравновесить давление, производимое на поршни снаружи.

При нагревании одного газа и охлаждении другого у каждого из них изменяются все три параметра состояния: давление, объем и температура.

Рассмотрим газ в левом сосуде. До нагревания он находился под давлением р₁, занимал объем V₁ и имел температуру Т₀; после нагревания эти параметры имеют значения р₂, V₂ и Т₁. Поскольку масса газа не менялась, то

(1)

До охлаждения газа в правом сосуде его давление, объем и температура имели значения р₁, V_l, Т₀; после охлаждения р₃, V₂, Т₂. Масса газа при нагревании не менялась, поэтому

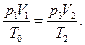(2)

Поскольку в обоих состояниях газов поршни находятся в равновесии, то должно быть в первом случае:

во втором: 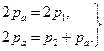(3)

Относительное изменение объема газа в цилиндре равно:

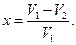(4)

Из уравнений (1)– (4) находим:

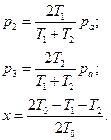
Пример 6. Сосуд емкостью 2V=2·10^-3 м³ разделен пополам полупроницаемой перегородкой. В одну половину сосуда введен водород массой m_в=2 г и азот массой m_а=28 г, в другой половине вакуум. Через перегородку может диффундировать только водород. Во время процесса поддерживается температура Т=373 К. Какие давления установятся в обеих частях сосуда?

Решение. При заполнении одной половины сосуда смесью газов молекулы водорода будут диффундировать через перегородку в другую половину сосуда до тех пор, пока давления водорода по обе стороны перегородки не сравняются. Так как перегородка делит сосуд на равные объемы и температура в них одна и та же, во вторую половину сосуда про диффундирует ровно половина начального количества водорода. После этого в одной части сосуда окажется смесь азота с водородом, в другой – про диффундировавший водород.

Для решения задачи нужно составить уравнение Менделеева – Клапейрона для каждого компонента газа: отдельно для азота и отдельно для водорода. Эти уравнения позволят определить давление каждого газа, после чего, используя закон Дальтона, легко найти давление смеси азота с водородом.

Если объем сосуда равен 2V, то в половине этого объема азот массой m_а при температуре Т будет производить давление р_а и

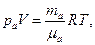(1)

где μ_а — киломолекулярная масса азота.

В том же объеме, при той же температуре после диффузии водород массой — будет производить давление р_в, причем

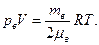(2)

Согласно закону Дальтона полное давление газа в этой части сосуда станет равным

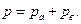(3)

По другую сторону перегородки давление водорода будет равно р_в.

При проведении числовых расчетов в задачах с применением уравнения Менделеева – Клапейрона приходится использовать киломолекулярные массы газов. В таблицах же даются значения атомных масс элементов. Поэтому, чтобы найти молекулярную и киломолекулярную массу того или иного газа, нужно прежде всего установить, сколько атомов входит в состав его молекулы. В нашей задаче, например, дается азот и водород. В свободном состоянии молекулы азота и водорода содержат не один, а два атома. Поэтому киломолекулярные массы этих газов будут равны соответственно μ_а=28 кг/кмоль и μ_в=2 кг/кмоль. Эти значения мы и должны взять при расчете.

Из уравнений (1)–(3)находим:

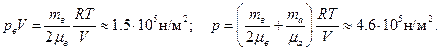
Пример 7.В откачанной ампуле объемом V=3 см³содержится радий массой m=5 г в течение времени τ=1 год. В результате радиоактивного распада из радия массой m₀ = 1 г в τ₀=1 сек вылетает n₀=3.7·10¹⁰ альфа-частиц, представляющих собой ядра гелия. Какое давление будет производить гелий при температуре Т=300 К?

Решение. Нам задано одно состояние гелия и дается ряд дополнительных условии, позволяющих определить массу газа. Для решения задачи нужно использовать основное уравнение газового состояния.

Если в закрытой ампуле объемом V находится v киломолей гелия под давлением р при температуре Т, то согласно уравнению Менделеева – Клапейрона

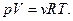
Число киломолей гелия, образовавшегося в результате рекомбинации альфа-частиц, вылетающих из радия, можно найти двумя путями: используя дополнительные условия задачи, определить массу гелия и, найдя в таблицах его молекулярную массу, разделить m на μ или по тем же дополнительным данным найти число атомов гелия N, образовавшихся в ампуле к интересующему нас моменту времени, и, зная число Авогадро N_A, определить v из формулы

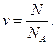
Воспользуемся вторым способом.

Если из радия массой m₀ за время τ₀ вылетает n₀ альфа-частиц, то из радия массой m за время τвылетит число частиц, равное

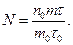
Число киломолей гелия, заключенного в ампуле, в этом случае равно:

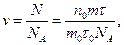
и уравнение состояния газа можно представить в окончательном виде так:

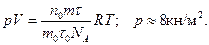
Пример 8.По газопроводной трубе идет углекислый газ под давлением р=392 кн/м² при температуре Т=280 К. Какова средняя скорость движения газа в трубе, если через поперечное сечение трубы, равное S=5 см², за τ=10 мин протекает газ массой m=20 кг?

Решение. В задаче рассматривается одно состояние равномерно движущегося газа с известным расходом. Поэтому, какой бы слой газа мы ни выбрали в движущемся потоке, параметры его состояния должны удовлетворить уравнению Менделеева – Клапейрона.

Выделим в трубе некоторый объем V, содержащий газ массой m, который весь проходит через поперечное сечение трубы S за время τ. Если этот газ находится под давлением р и имеет температуру Т, то

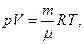(1)

где μ=44 кг/кмоль – киломолекулярная масса углекислого газа С0₂.

Объем газа можно выразить через сечение S и высоту выделенного цилиндра: V=Sl. За время τ через сечение трубы проходит весь газ, заключенный в объеме этого цилиндра, поэтому при скорости υ движения газа должно быть l= υτ и

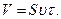(2)

Решение уравнений (1)–(2) относительно скорости движения газа дает:

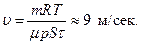
Пример 9. Сколько гелия потребуется для наполнения воздушного шара диаметром d=10 м, чтобы шар мог поднять груз весом Q=9.8 кн при нормальном атмосферном давлении и температуре Т=290 К? Объемом груза пренебречь.

Решение. Для подъема воздушного шара необходимо, чтобы вес вытесненного им воздуха m_вg был больше или в крайнем случае равен весу газа m_гg, наполняющего оболочку шара, и весу Q его оснастки, т. е.

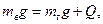(1)

где m_в – масса воздуха, вытесненного шаром; m_г – масса газа (гелия), наполняющего оболочку.

Если бы масса воздуха m_в была известна, то из этого уравнения можно было бы определить массу гелия. Чтобы найти m_в, воспользуемся уравнением Менделеева — Клапейрона.

Воздух, окружающий шар, находится под атмосферным давлением рй и имеет температуру Т, поэтому для воздуха, занимающего объем оболочки Уш> уравнение газового состояния дает:

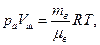(2)

где μ_в=29 кг/кмоль.

И наконец, последним соотношением, которое нужно использовать в решении, является формула:

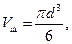(3)

поскольку нам известен диаметр воздушного шара d, а не его объем. Из уравнений (1)–(3) находим массу гелия:

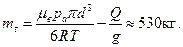
Пример 10. В цилиндре с площадью основания S =100 см² находится воздух при температуре Т=290 К. На высоте Н=0.60 м от основания цилиндра расположен легкий поршень, на котором лежит гиря массой m=100 кг. Какую работу совершит газ при расширении, если его нагреть на ΔT=50°C? Атмосферное давление р_а = 10⁵ н/м².

Решение. В процессе нагревания газ расширяется и совершает работу по преодолению силы тяжести груза и силы атмосферного давления, действующих на поршень. Так как эти силы постоянные, то при достаточно медленном нагревании газ будет расширяться изобарически и его работу можно вычислить по формулам;

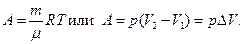
По условию задачи нам задан объем газа в исходном состоянии, но не указано, что это за газ. Поэтому нужно воспользоваться второй формулой.

Если при температуре Т₁ газ занимал объем V₁, а после нагревания до температуры Т₂ стал занимать объем V₂, то работа расширения равна:

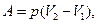
где р – давление, производимое газом на поршень.

При равновесии поршня это давление в каждый момент времени уравновешено атмосферным давлением р_а, и давлением (mg/S) создаваемым гирей:

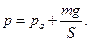(2)