Практичне заняття 20. критерій згоди пірсона

Приклад. В таблиці наведено відхилення (в мк) діаметрів виготовлених на верстаті валків від заданого розміру

0-5	5-10	10-15	15-20	20-25

Вибіркове середнє дорівнює 11,8 мк., а вибіркове стандартне відхилення – 4,7 мк.. Розрахувати теоретичні частоти попадання у відповідні інтервали варіаційного ряду, вважаючи розподіл діаметрів валків нормальним, а його параметри рівними їхнім оцінкам за вибіркою.

Розв’язання. Розрахуємо теоретичні частоти нормального розподілу, вважаючи параметри розподілу відомими і рівними їх оцінкам за вибіркою: мк., мк., . Теоретичні ймовірності попадання випадкової величини 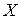в інтервали рівні , де – функція Лапласа, а кінці інтервалів обчислені за формулами , причому найменше значення рівне , а найбільше . Теоретичні частоти .

Складемо розрахункову таблицю

				–1,45	–0,5000	–0,4265	0,0735	18,375
			–1,45	–0,38	–0,4265	–0,1480	0,2785	69,625
			–0,38	0,68	–0,1480	0,2517	0,3997	99,925
			0,68	1,74	0,2517	0,4591	0,2074	51,85
			1,74		0,4591	0,5000	0,0409	10,225
							1,0000

Приклад. Вимірювання зросту юнаків віком 17 років дав такі результати:

h = 4 cм	154-158	158-162	162-166	166-170	170-174	174-178	178-182	182-186
ni

Визначити гіпотетично, який закон розподілу має ознакa Х – зріст юнака. При рівні значущості a = 0,01 перевірити правильність висунутої нульової гіпотези.

Розв’язання. Для заданого статистичного розподілу побудуємо гістограму частот (рис. 143).

Рис. 143

За формою гістограми частот можемо припустити, що ознака Х має нормальний закон розподілу. Отже, висуваємо нульову гіпотезу Н₀: ознака Х має нормальний закон розподілу ймовірностей.

Для перевірки правильності Н₀ використаємо критерій згоди Пірсона.

Отже, необхідно обчислити теоретичні частоти, а для цього знайдемо значення , побудувавши дискретний розподіл за заданим інтервальним, а саме:

xi
ni

cм;

см.

Обчислення теоретичних частот наведено в таблиці:

xi	xi+1	ni
			– 2,04	– 1,42	– 0,4793	– 0,4222
			– 1,42	– 0,79	– 0,4222	– 0,2852
			– 0,79	– 0,16	– 0,2852	– 0,0636
			– 0,16	0,464	– 0,0636	0,1772
			0,464	1,09	0,1772	0,3621
			1,09	1,72	0,3621	0,4573
			1,72	2,34	0,4573	0,4904
			2,34	2,97	0,4904	0,4986

Обчислення спостережуваного значення наведено в таблиці:

ni	npi	ni – npi	(ni – npi)2
				0,667
		– 2		0,182
				2,667
		– 7		2,579
		– 2		0,4
				0,333

.

За таблицею (додаток 8) знаходимо значення

Критична область зображена на рис. 144.

Рис. 144

Висновок. Оскільки , немає підстав для відхилення нульової гіпотези Н₀ про нормальний закон розподілу ймовірностей ознаки Х.

Приклад. За заданим статистичним розподілом вибірки:

h = 4 cм	0-10	10-20	20-30	30-40	40-50
ni

з’ясувати гіпотетично закон розподілу ймовірностей випадкової величини Х. При рівні значущості a = 0,01 перевірити правильність цього припущення.

Розв’язання. Для визначення закону розподілу ознаки Х побудуємо гістограму частот (рис. 145).

Рис. 145

За формою гістограми частот можна гіпотетично стверджувати, що ознака Х має експоненціальний закон розподілу ймовірностей.

Для перевірки правильності цього твердження використаємо критерій згоди Пірсона. Теоретичні частоти в цьому разі обчислюються за формулою

,

де .

Отже, необхідно обчислити , побудувавши дискретний статистичний розподіл за наведеним інтервальним, а саме:

xi
ni

Оскільки 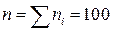, то

.

Тоді .

Обчислення теоретичних частот наведено в таблиці:

xi	xi+1	ni
				0,522
			0,522	0,273
			0,273	0,142
			0,142	0,074
			0,074	0,0039

Обчислення спостережуваного значення критерію наведено в таблиці:

ni	npi	ni – npi	(ni – npi)2
		–8		1,33
				3,77
		– 1		0,14
		– 3		1,29

.

За таблицею (додаток 8) знаходимо значення критичної точки

.

Критичну область зображено на рис. 146.

Рис. 146

Висновок. Оскільки , нульова гіпотеза про експоненціальний закон розподілу ознаки Х приймається.