Теорема о сложении ускорений

Определим зависимость между относительным, переносным и абсолютным ускорением точки. На основании равенства (84) при дифференцировании по времени можно записать

. (86)

Примем, что при относительном движении вектора относительной и переносной скорости получат изменения и соответственно; при переносном движении вектора относительной и переносной скорости получат изменения и

. (87)

Относительное ускорение характеризует изменение относительной скорости только при относительном движении, поэтому

. (88)

Переносное ускорение характеризует изменение переносной скорости только при переносном движении, поэтому

. (89)

В результате получаем

. (90)

Введем обозначение

. (91)

Величина , характеризующаяся изменением относительной скорости точки при переносном движении, и переносной скорости точки при ее относительном движении, называется поворотным или кориолисовым ускорением точки.

Равенство (86) примет вид

. (92)

Полученное уравнение выражает теорему Кориолиса о сложении ускорений: при сложном движении ускорение точки равно геометрической сумме трех ускорений: относительного, переносного и кориолисова (поворотного).

Определим кориолисово ускорение при поступательном и вращательном движении подвижной системы О₁х₁у₁z₁ (рис. 45). Движение подвижной системы определяется поступательным движением системы отсчета (перемещение ) и вращением системы относительно оси (характерные скорости определяются угловой скоростью 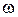). Вектор 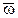представляет собой переносную угловую скорость .

Рис.45.

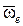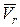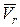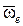Вектор получит приращение в переносном движении ; – скорость, с которой перемещается точка М при повороте вектора вокруг точки с угловой скоростью . В результате получаем

. (93)

Тогда переносная скорость равна геометрической сумме вектора скорости полюса точки О₁ и вектора переносной скорости точки при ее относительном движении

. (94)

За промежуток времени

. (95)

. (96)

Кориолисово ускорение составит

. (97)

Кориолисово ускорение равно удвоенному произведению векторов переносной угловой скорости (подвижной системы) и относительной скорости точки.

Численное значение кориолисова ускорения определяют

. (98)

где 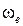– угловая скорость подвижной системы;

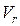– скорость точки в относительном движении;

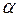– угол между векторами 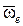и .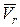

Вектор кориолисова ускорения направлен перпендикулярно плоскости, проходящей через векторы 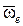и 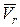в сторону действия угловой скорости 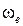в переносном движении (рис.46).

В случае поступательного переносного движения, угловая скорость подвижной системы равна нулю , тогда абсолютное ускорение составит

Рис.46.

. (99)

При поступательном переносном движении абсолютное ускорение точки равно геометрической сумме относительного и переносного ускорений.

Практическая работа 4