Характерные объекты управления
Как мы уже говорили, в зависимости от того, что из себя представляет объект управления и от того какие цели преследуются при его моделировании, создаются модели в различных формах, в моделях отражаются различные самые важные для исследователя свойства объекта-оригинала. Кроме того, при решении одной и той же задачи на разных этапах могут использоваться разные модели. На ранних – более простые, потом – более подробно описывающие свойства объекта. Усложнение позволяет оценить влияние тех свойств объекта или системы, которые раньше рассматривались как несущественные.
К моделям предъявляются противоречивые требования. С одной стороны, она должна как можно лучше отражать свойства реальных объекта или системы, т.е. быть достаточно сложной. С другой стороны, она должна быть достаточно простой, чтобы задачу разработки системы можно было провести достаточно просто и за приемлемое время.
Как уже отмечалось, нас будут интересовать в качестве объектов антропогенные объекты. В основном мы будем иметь дело с исследованием различных технологических агрегатов (или их совокупностью), в которых происходят физические или химические процессы (теплообменные, массообменные, тепломассообменые, электромеханические) для получения продукта с заданными свойствами – технологические процессы.
(Например, объекты, рассмотренные вами на ознакомительной практике - нагревательная печь, сосуд, наполняемый жидкостью, пропариватель. Электронагревательная печь – это технологический агрегат, для проведения в нем технологического процесса нагрева продукта. Сосуд с жидкостью – технологический агрегат, в котором происходит процесс накопления (слива) жидкости. Пропариватель – технологический агрегат, для проведения технологического процесса пропаривания продукта).
Основной целью исследования этих объектов будет построение систем управления ими. Важной особенностью этих объектов для нас является то, что они являются динамическими, т.е. параметры процессов, протекающих в этих объектах, определенным образом изменяются во времени (уровень в баке, сток и приток жидкости в бак, температура в печи и т.д.). Поэтому принципиальным требованием к моделям таких объектов является отражение динамики во взаимосвязи между входными и выходными переменными. Следовательно, входные и выходные переменные должны рассматриваться как процессы (т.е. как функции времени). А модели преобразования процессов (т.е. связь между входными и выходными переменными) должны представляться в форме дифференциальных уравнений (содержащих одну или несколько функций и их производных по времени) или разностных уравнений (когда описание ведется в дискретном времени и производные заменяются конечными разностями).
Рассмотрим некоторые примеры.
Пример№1. В бак по трубопроводу поступает жидкость, приток которой изменяется вентилем (краном). Из бака жидкость откачивается насосом, который имеет постоянную производительность. Разность 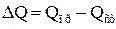 влияет на уровень L в баке.
влияет на уровень L в баке.
Можем составить структурную схему такого объекта.
 |
Рис. 3.1
Скорость изменения уровня пропорциональна 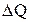 и обратно пропорциональна площади поперечного сечения бака F. Это утверждение математически можно записать так:
и обратно пропорциональна площади поперечного сечения бака F. Это утверждение математически можно записать так: 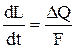 .
.
Если принять L=y; 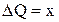 ;
; 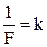 , то получаем следующее дифференциальное уравнение:
, то получаем следующее дифференциальное уравнение:
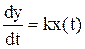
или
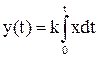
Из последнего уравнения видно, что выходная величина (изменение уровня во времени) пропорциональна интегралу от входной величины (интегралу изменения разности притока и стока).
Рассмотренный пример показывает, что бак является динамическим объектом, динамику между входными и выходными переменными описывает полученное ДУ.
Итак, необходимо понимать, что в дальнейшем мы будем моделировать динамические объекты и системы, которые описываются дифференциальными уравнениями. В качестве инструмента моделирования, мы будем использовать математическую систему компьютерной математики Matlab и ее пакет расширения Simulink, как удобное средство для моделирования динамических систем, в котором практически отсутствуют ограничения на вид дифференциальных уравнений.
ЛЕКЦИЯ №4
